當電路頻率相同時,相量是分析交流電路中元件行為的有效方法。 兩個向量相加的結果取決于它們的相對相位,它們是“同相”還是“異相”,因為存在一些相位差。
正弦波形是一種交變量,可以在時域中沿水平軸以圖形方式呈現。 作為時變量,正弦波形在時間 π/2 處具有正最大值,在時間3π/2處具有負最大值,零值沿基線出現在0、π和2π點。
然而,并不是所有的正弦波形都會同時準確地通過零軸點,而是與另一個正弦波相比可能會向右或向左“偏移” 0 o某個值。
例如,將電壓波形與電流波形進行比較。 然后這會在兩個正弦波形之間產生角度偏移或相位差。 在t = 0時不通過零的任何正弦波都具有相移。
正弦波形的差異或相移也稱為角度Φ(希臘字母 Phi),以度數或弧度表示波形從某個參考點沿水平零軸移動。 換句話說,相移是兩個或多個波形沿公共軸的橫向差異,相同頻率的正弦波形可以具有相位差。
相位之間的差異,交變波形的Φ可以在0到其最大時間周期之間變化,在一個完整的周期內,波形的T可以在水平軸上的任何位置,Φ = 0 到 2π(弧度)或Φ = 0 到 360 o取決于所使用的角度單位。
相位差也可以表示為τ的時間偏移(以秒為單位,代表時間段的一部分),例如T,+10mS 或 – 50uS,但通常更常見的是將相位差表示為角度測量值。
然后我們在之前的正弦波中開發的正弦電壓或電流波形的瞬時值方程將需要修改以考慮波形的相位角,這個新的通用表達式變為。
相位差方程
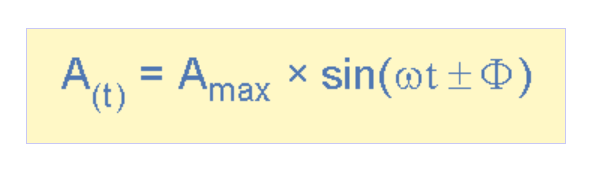
在哪里:
A m – 是波形的幅度。
ωt – 是以弧度/秒為單位的波形角頻率。
Φ (phi) – 是波形從參考點向左或向右移動的相位角,以度或弧度為單位。
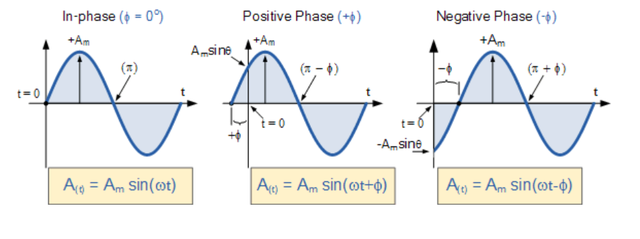
如果正弦波形的正斜率在t = 0 “之前”通過水平軸,則波形已向左移動,因此Φ > 0,并且相位角本質上將為正,+Φ給出超前相位角。 換句話說,它出現的時間早于 0 o,產生矢量的逆時針旋轉。
同樣,如果正弦波形的正斜率在t = 0 “之后”的某個時間通過水平 x 軸,則波形向右移動,因此Φ < 0,并且相位角本質上將為負-Φ產生滯后的相位角,因為它出現的時間晚于 0 o,產生矢量的順時針旋轉。 兩種情況如下所示。
正弦波形的相位關系
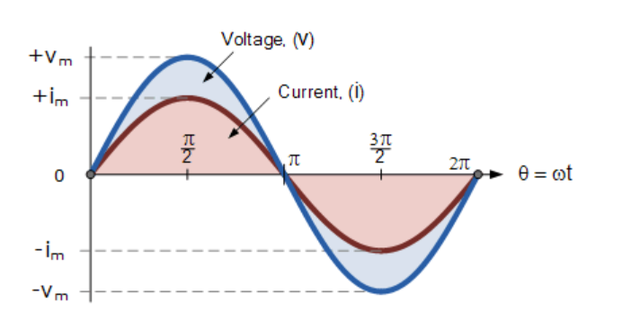
首先,讓我們考慮兩個交變量,例如電壓v和電流i具有相同的頻率?以赫茲為單位。 由于這兩個量的頻率與角速度相同,因此ω也必須相同。 所以在任何時刻我們都可以說電壓的相位v將與電流的相位相同i。
那么特定時間段內的旋轉角度將始終相同,因此v和i兩個量之間的相位差將為零且Φ = 0。 由于電壓v和電流i的頻率相同,因此它們必須在一個完整的周期內同時達到其最大正值、負值和零值(盡管它們的幅度可能不同)。 那么這兩個交變量v和i被稱為“同相”。
兩個正弦波形——“同相”
現在讓我們考慮電壓v和電流i之間有30 o的相位差 ,因此(Φ = 30 o或π /6弧度)。 由于兩個交變量以相同的速度旋轉,即它們具有相同的頻率,因此該相位差將在所有瞬間保持恒定,則 兩個量之間的30 °相位差由 phi 表示, Φ如下所示。
正弦波形的相位差
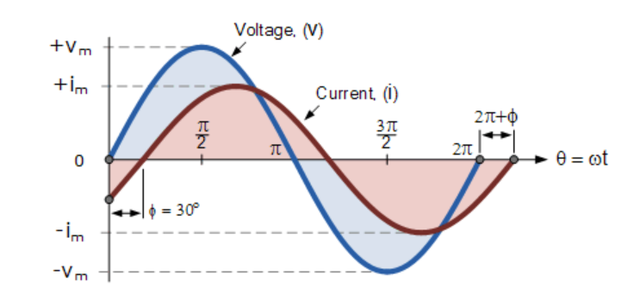
上面的電壓波形沿水平參考軸從零開始,但在同一時刻,電流波形的值仍然為負,并且直到30 o之后才穿過該參考軸。 然后當電流穿過水平參考軸在電壓波形之后達到其最大峰值和零值時,兩個波形之間存在相位差。
由于兩個波形不再“同相”,因此它們必須“異相”,其大小由 phi, Φ決定,在我們的示例中為30 o。 所以我們可以說這兩個波形現在是30 o異相。 也可以說電流波形“滯后”于電壓波形相角Φ。 然后在我們上面的示例中,兩個波形具有滯后相位差,因此上面的電壓和電流的表達式將給出為。
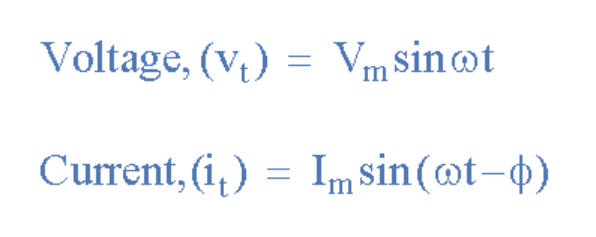
其中電流i “滯后”電壓v相位角Φ
同樣,如果電流i具有正值并穿過參考軸,在電壓v之前的某個時間達到其最大峰值和零值,則電流波形將“超前”電壓某個相位角。 然后這兩個波形被稱為具有超前相位差,電壓和電流的表達式都是。
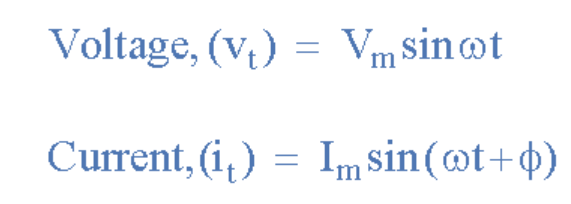
其中電流i “超前”電壓v相位角Φ
正弦波的相位角可用于描述一個正弦波與另一個正弦波的關系,使用術語“超前”和“滯后”來表示繪制在同一參考軸上的兩個相同頻率的正弦波形之間的關系. 在我們上面的示例中,兩個波形異相30 o。 所以我們可以正確地說i滯后v或者我們可以說v領先i 30 o,這取決于我們選擇哪個作為我們的參考。
可以沿水平零軸的任何位置測量兩個波形之間的關系和產生的相位角,每個波形以“相同斜率”方向通過,無論是正向還是負向。
在交流電源電路中,這種描述同一電路內電壓和電流正弦波之間關系的能力非常重要,并且構成了交流電路分析的基礎。
余弦波形
所以我們現在知道,如果與另一個正弦波相比,一個波形向0 o的右側或左側“移動”,則該波形的表達式變為A m sin(ωt ± Φ )。 但是,如果波形在參考波形之前以正向斜率90 o或π /2弧度穿過水平零軸,則該波形稱為余弦波形,表達式變為。
余弦表達式
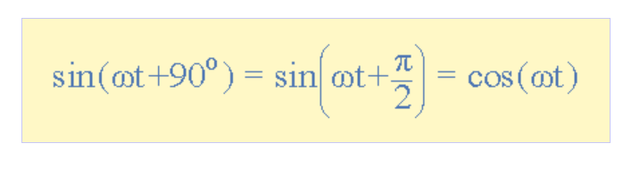
余弦波,簡稱“cos”,在電氣工程中與正弦波一樣重要。 余弦波與其對應的正弦波具有相同的形狀,即它是一個正弦函數,但在它之前移動了+90 o或一個完整的四分之一周期。
正弦波和余弦波的區別
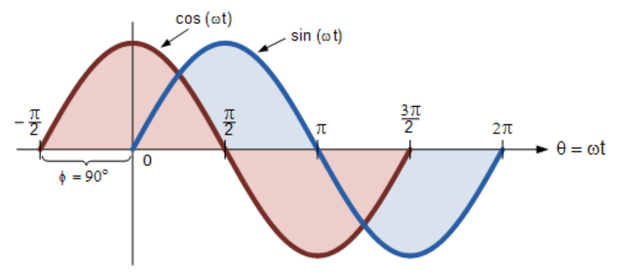
或者,我們也可以說正弦波是在另一個方向上偏移了-90 o的余弦波。 無論哪種方式,在處理具有角度的正弦波或余弦波時,始終適用以下規則。
正弦波和余弦波關系
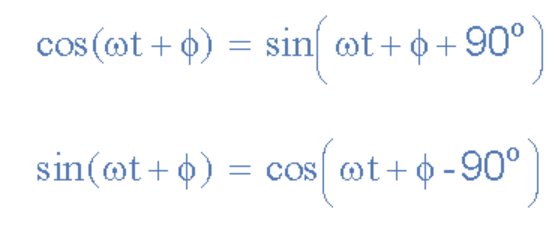
比較兩個正弦波形時,更常見的是將它們的關系表示為具有正向振幅的正弦或余弦,這是使用以下數學恒等式實現的。 通過使用上面的這些關系,我們可以將具有或不具有角度或相位差的任何正弦波形從正弦波轉換為余弦波,反之亦然。
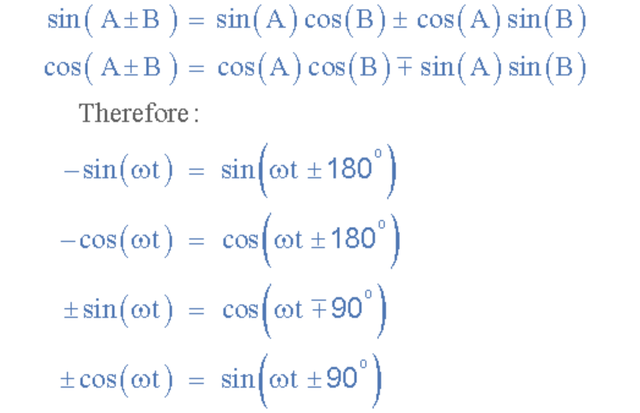
在下一個關于向量的教程中,我們將使用圖形方法來表示或比較兩個正弦波之間的相位差,方法是查看單相交流量的向量表示以及與兩個或多個向量的數學加法相關的一些向量代數。
-
電路
+關注
關注
173文章
5998瀏覽量
173848 -
正弦波
+關注
關注
11文章
649瀏覽量
56014 -
波形
+關注
關注
3文章
384瀏覽量
31862 -
交流電路
+關注
關注
0文章
185瀏覽量
29024 -
相位差
+關注
關注
1文章
31瀏覽量
15226
發布評論請先 登錄
相關推薦
電源技術之正弦波形(二)
依相位平衡條件判定正弦波振蕩電路振蕩的簡明方法
標準正弦波形500W雙重絕緣逆變器MEM-4105/4205
對非整周期正弦波形信噪比計算方法的研究

正弦波發生電路原理
如何使用傅立葉分析各種非正弦波形中諧波分量的幅度及相位關系


















評論