實例分析：

帶有正反饋，負反饋，信號線交叉的結構圖簡化：

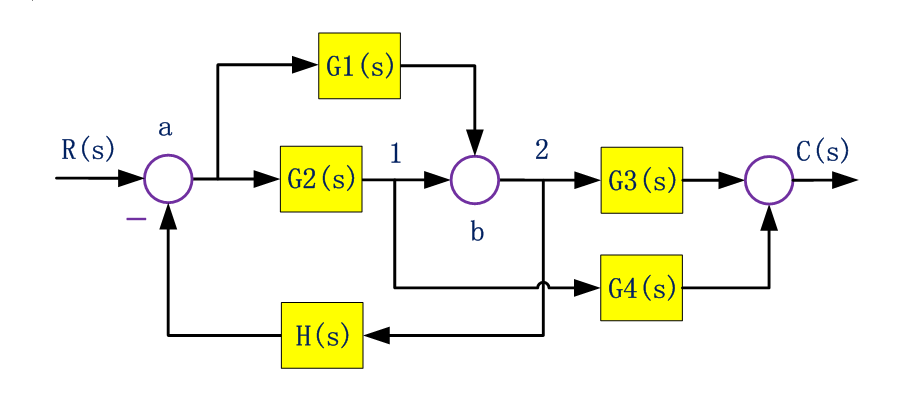
比較點ab之間是一個并聯方框連接，引出點1夾在兩個比較點a,b之間，G1G2無法并聯簡化，需要把引出點1移動。

引出點不能與比較點交換，因此只能往前移動到a后面、G2前面的位置；

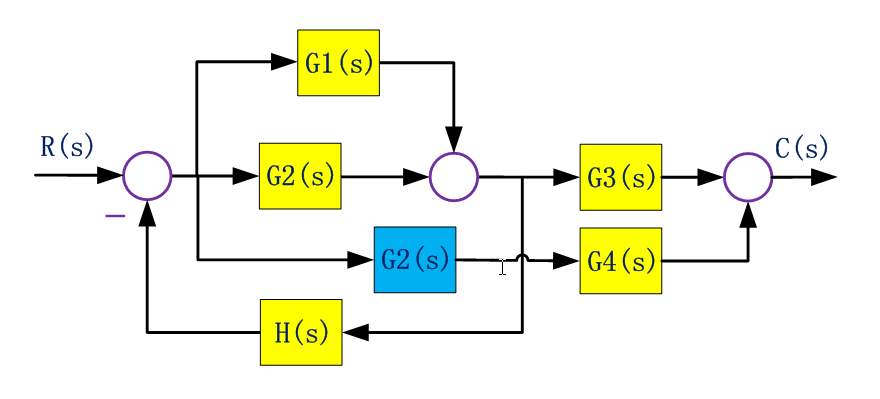
把G1,G2并聯方框簡化，把G2G4串聯方框簡化，沒有標明符號的比較點都是默認正反饋：

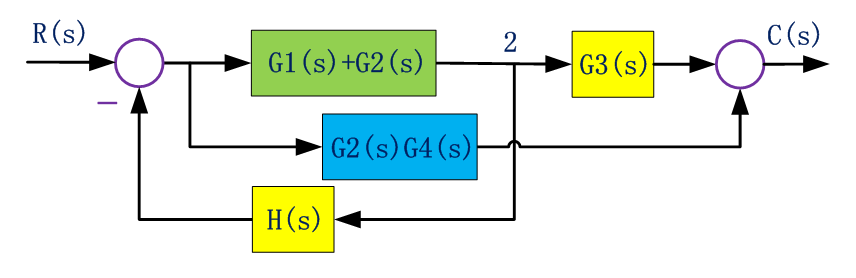
把引出點2前移，使得H負反饋回路不交叉：

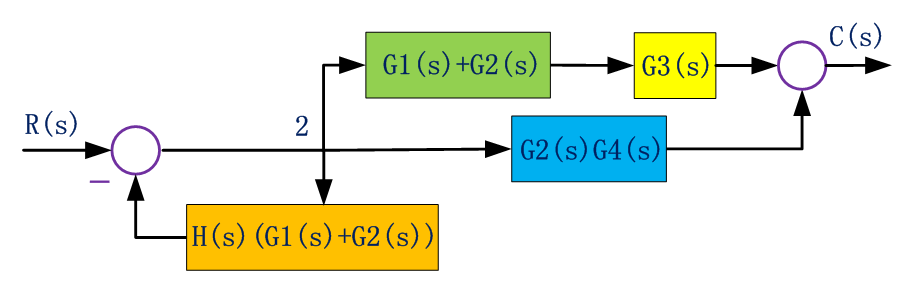
簡化負反饋連接方框：

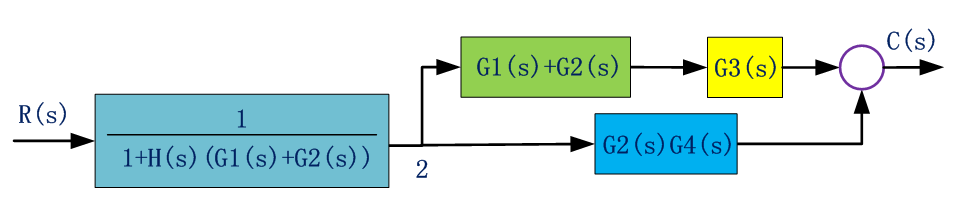
由此，簡化后方框之間的連接關系是簡單的串并聯關系，最后化簡為：

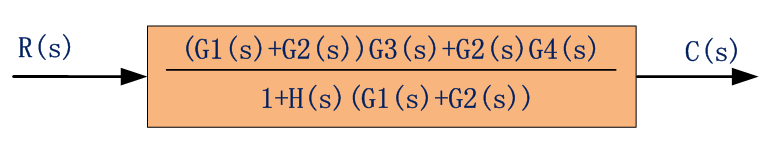
信號流圖的組成及其性質

信號流圖起源于梅森利用圖示法來描述一個或一組線性代數方程式，他是由節點和支路組成的一種信號傳遞網絡；

節點用小圓圈表示，代表方程式中的變量。支路是連接兩個節點的定向線段，用支路增益表示方程式中兩個變量的因果關系，因此把支路稱為乘法器。

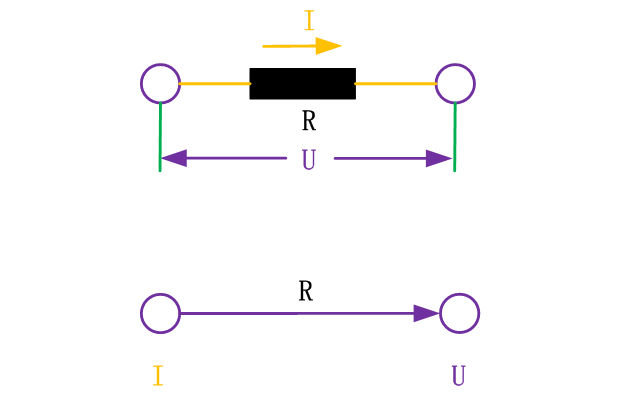
以電阻元件為例，電阻流過的電流為I，電阻兩端的電壓為U，電阻為R。

電阻滿足歐姆定律：U=IR。如果定義電流I為輸入，輸出為電壓U，支路增益為R，就可以用信號流圖形式表示電阻元件；

歸納：

1 節點標志系統的變量。每個節點標志的變量是所有流向該節點的信號之代數和。從同一節點流向各支路的信號均用該節點的變量表示。

2 支路相當于乘法器，信號流經支路時，被乘以支路增益而變換為另一信號。

3 信號在支路上只能沿箭頭方向傳遞。

4 對于給定的系統，節點變量的設置是任意的，信號流圖不唯一。

術語：

源節點（輸入節點）：在源節點上，只有信號輸出的支路，而沒有信號輸入的支路，它一般代表系統的輸入變量，故也稱為輸入節點。

阱節點（輸出節點）：在阱節點上，只有輸入支路， 沒有輸出支路，一般代表輸出變量故也稱為輸出節點；

混合節點：既有輸入支路又有輸出支路。

前向通道：信號從輸入節點到輸出節點傳遞時，每個節點只通過一次的通路。前向通路上各支路增益乘積稱為前向通道總增益。

回路：起點和終點在同一個節點，而且信號通過每一個節點不多于一次的閉合通路。

不接觸回路：回路之間沒有公共節點。

信號流圖繪制：

任何線性數學方程都可以用信號流圖表示，對于含有微分或積分的線性方程，通常經過拉氏變換，允許考慮非零初始條件，將微分方程變換為s的代數方程后再畫信號流圖。

繪圖步驟：對系統中每個變量指定一個節點，按變量因果關系從左到右順序排列；用標明支路增益的支路，根據數學方程式將各節點變量正確連接。

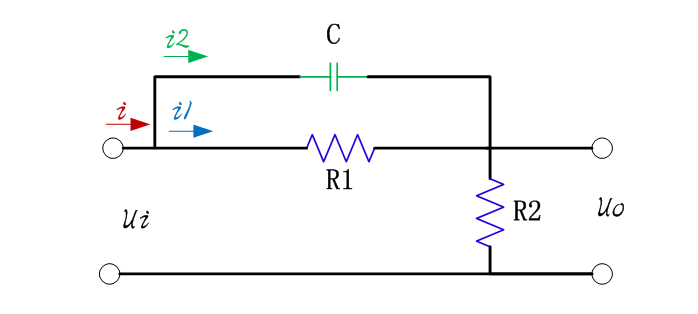
已知系統結構圖：信號線上標記傳遞的信號，方框是對變量進行變換或運算的算子。

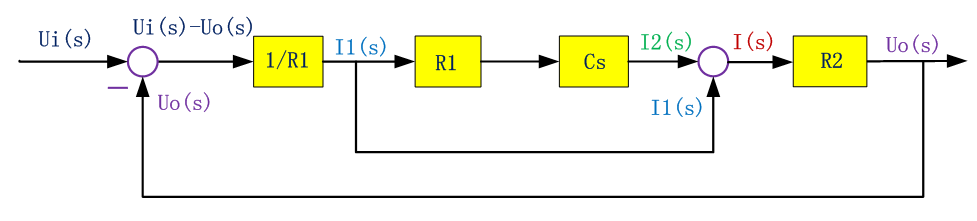
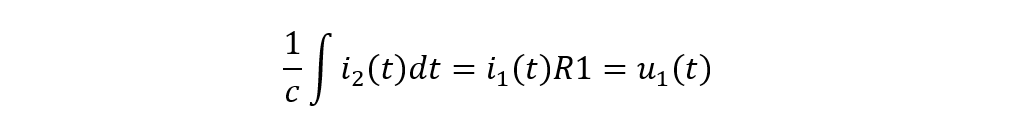
設電容C兩端電壓為u1(t),考慮初始電壓u1(0),

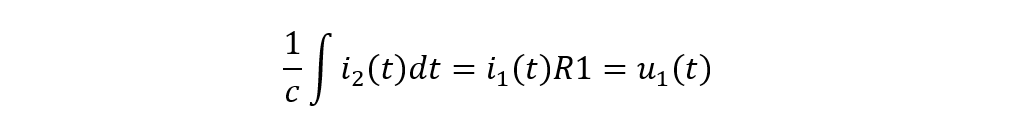
等式求取拉氏變換，

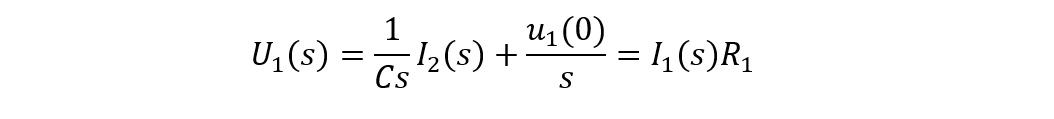
可求出非初始條件下，電容電流I2(s)：

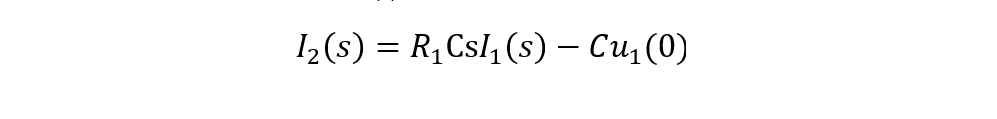
繪制信號流圖：把結構圖中信號線用小圓圈代替，表示傳遞的信號，方框用標有傳遞函數的有向線段代替，表示帶有增益的支路。

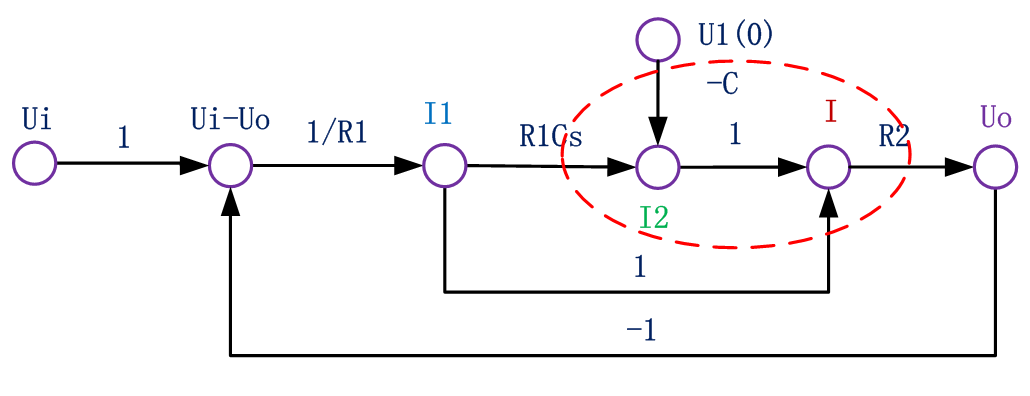
注意，在比較點之前有比較點或引出點的情況，需要各設置一個節點，分別標志兩個變量，它們之間的支路增益是1。

梅森增益公式：

利用梅森Mason增益公式直接求取從源節點到阱節點的傳遞函數。當不考慮非零初始條件時，也可用Mason公式計算系統結構圖的傳遞函數。

梅森增益公式可以用克萊姆法則求解線性方程組獲得；

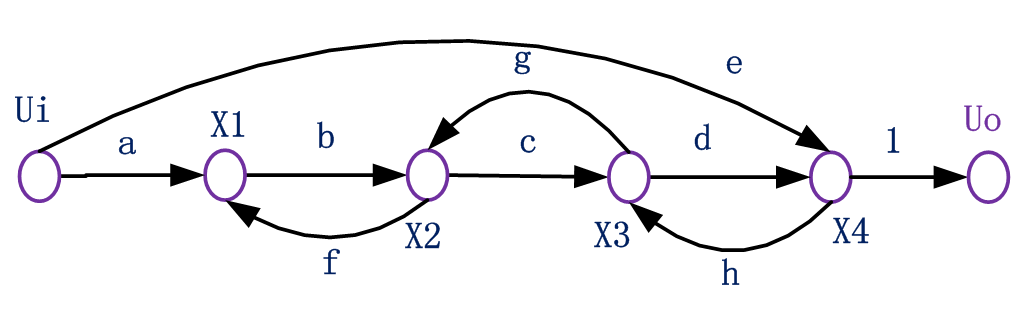
根據信號流圖，列寫變量代數方程：

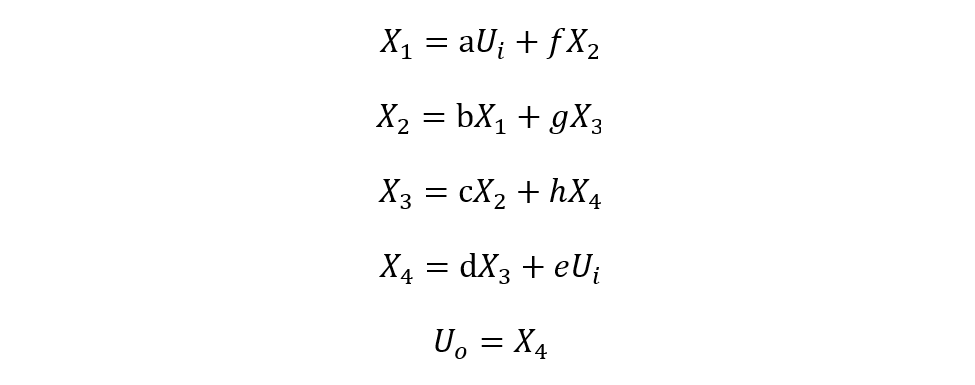
把輸入量提到公式右側，左側為待求變量：

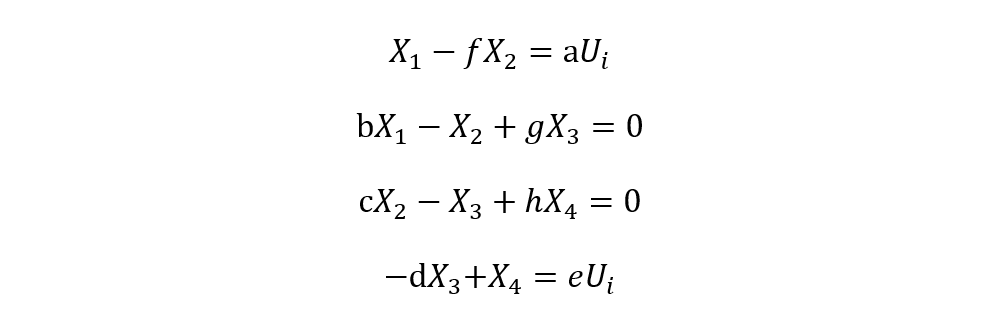
對于線性系統，可直接求取上述非齊次線性方程的解：

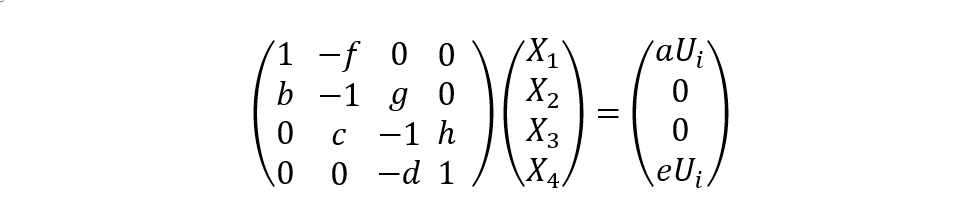
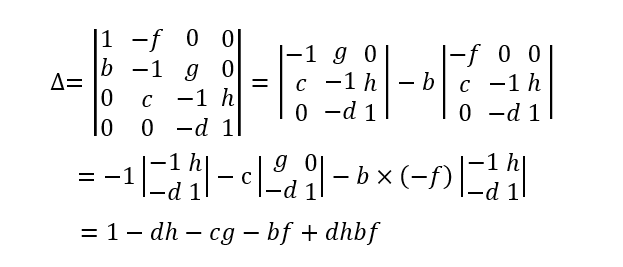
方程系數矩陣行列式值：

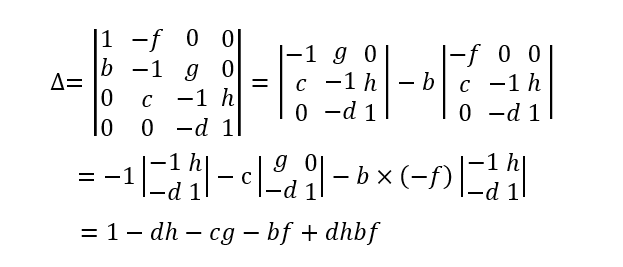
用方程右側自由項替換矩陣第四列，求對應行列式值：

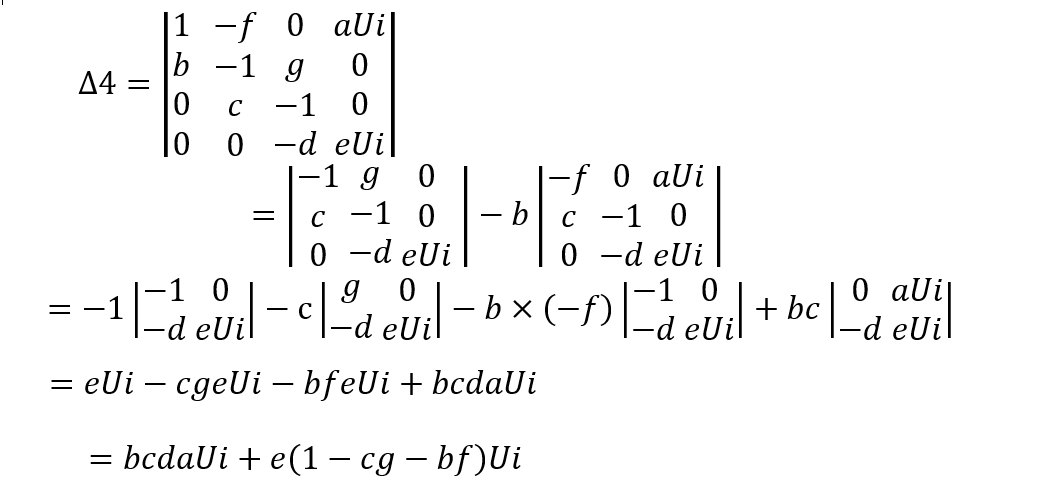
由克萊姆法則可求出X4及系統傳遞函數：

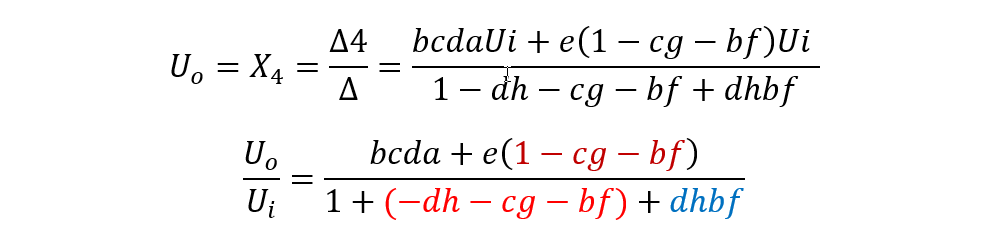
梅森公式具有一般性：

1 傳遞函數分母多項式是系統參數構成的系數行列式，分子多項式用自由項替換與輸出變量對應的列向量對應的行列式。

2 分母多項式包含所有獨立回路增益之和，所有互不接觸單獨回路增益乘積之和，增益符號為-1，N個單獨回路增益相乘相當于符號為（-1）N。

比如上式中，分母多項式的dh,cg,bf前的符號為負，dhbf前的符號為正。

3 分子多項式包含前向通道總增益減去與前向通道不接觸回路的回路增益乘以該前向通道總增益，簡化表達式為前向通道總增益乘以分母多項式去掉所有與該前向通道接觸的回路增益項后的余項式；

比如上式中，分子多項式所包含的前向通道增益e，與cg和bf不接觸，因此可以把分母多項式中包含的dh看做為0，去掉與0相關的所有項后，獲得不接觸回路余項式為1+（-cg-bf）

用梅森公式計算系統傳遞函數：

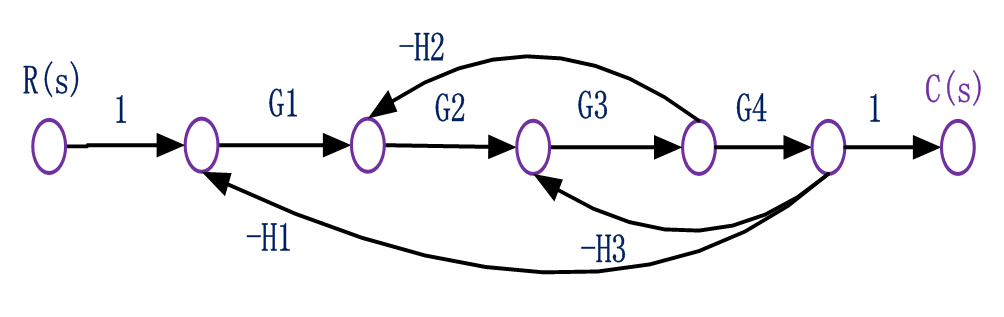
這個系統有一個前向通道，三個接觸單獨反饋回路；

因此，分子多項式只包含前向通道增益，余因子式為1；

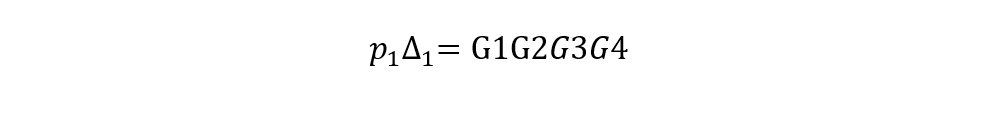
分母多項式：所有回路互相接觸，因此只包含所有單獨回路的增益之和；

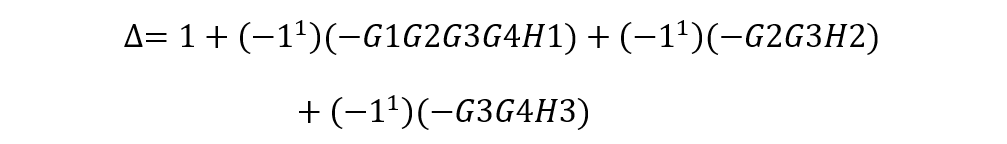
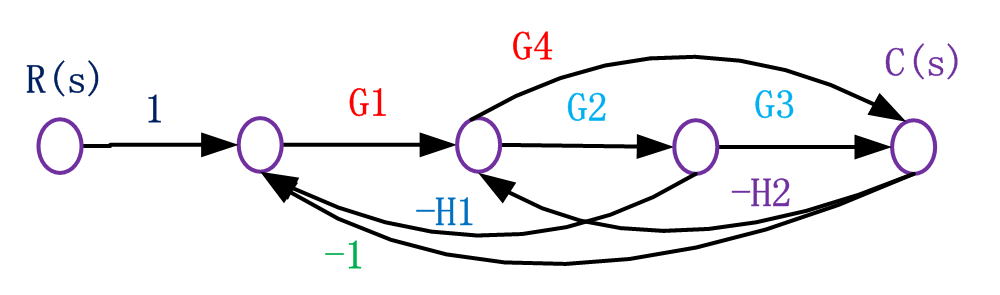
這個信號圖含有兩個前向通道，前向通道增益分別為P1=G1G2G3,P2=G1G4;

有五個單獨回路，與前向通道G1G2G3相關的獨立回路L1=-G1G2H1,L2=-G2G3H2,L3=-G1G2G3,與前向通道G1G4相關的獨立回路：L4=-G4H2,L5=-G1G4；

不接觸回路為零；

分子多項式為：兩個前向通道的余因子式都為1

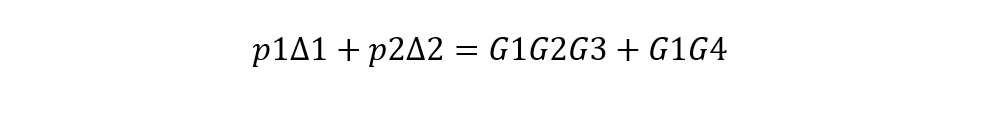
分母多項式為：所有回路互相接觸，因此只包含所有單獨回路的增益之和；

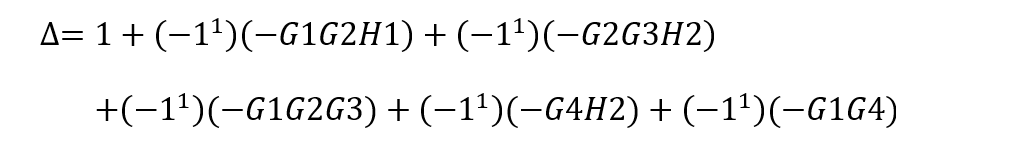
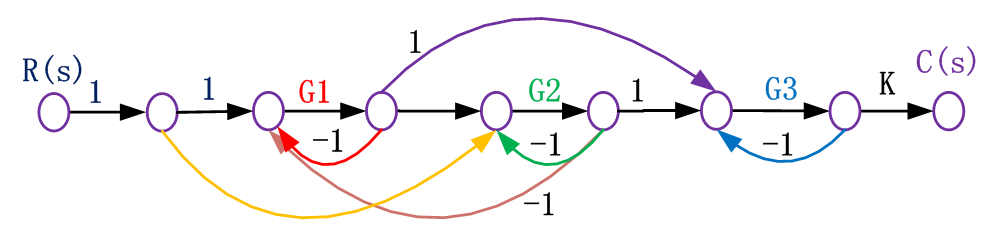
這個信號圖中，單獨回路有四個：G1，G2，G3，G1G2

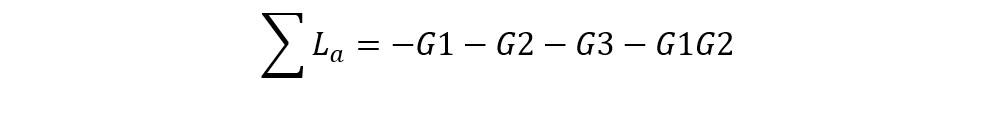
兩兩互不接觸回路有四組：

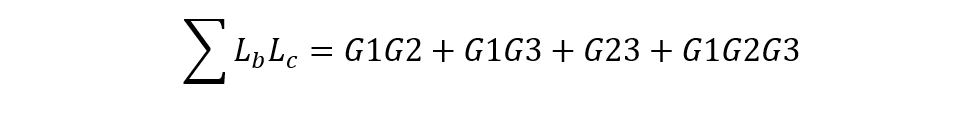
三個互不接觸回路有一組：

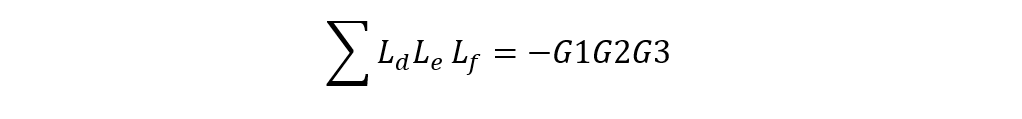
因此，分母多項式為：

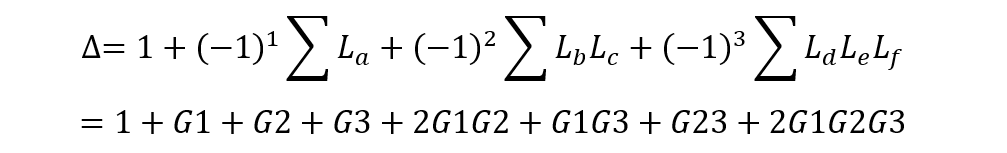
從源節點R到阱節點C的前向通道共有四條，前向通道增益及余因子式分別為：

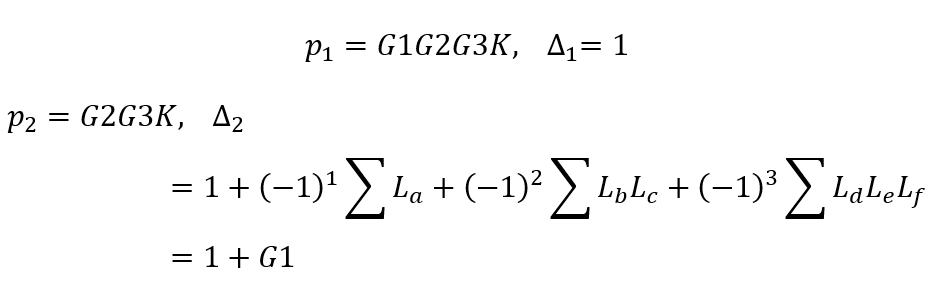
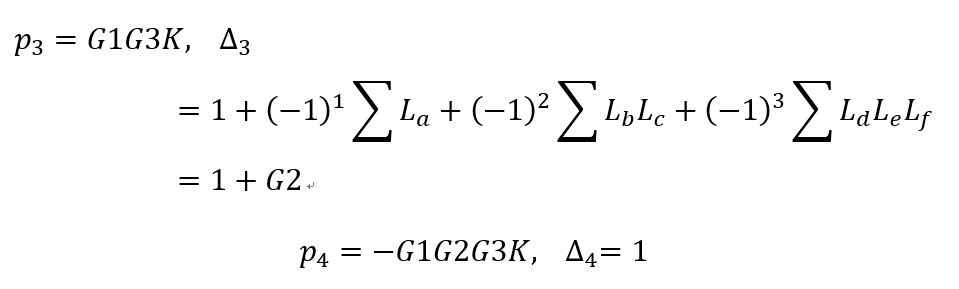
第四個前向通道比較特殊，不接觸回路為零。

系統傳遞函數為：

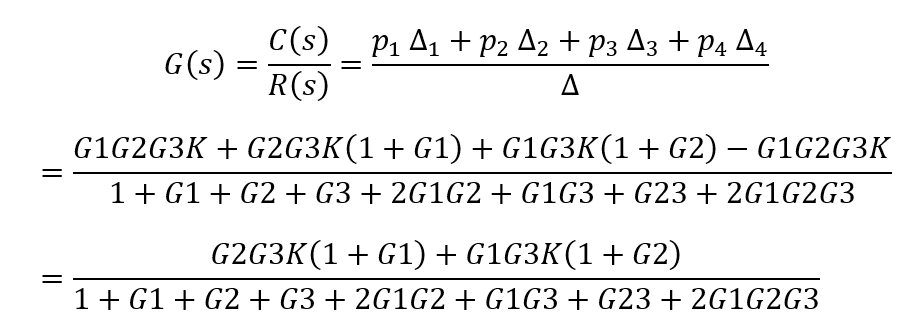
用梅森公式校驗系統結構圖的傳遞函數：

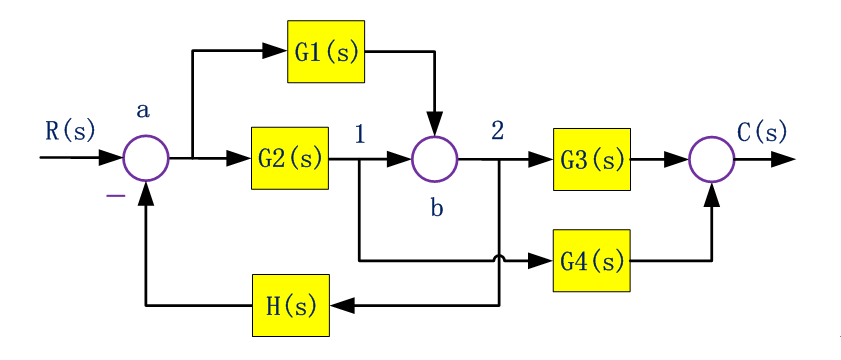
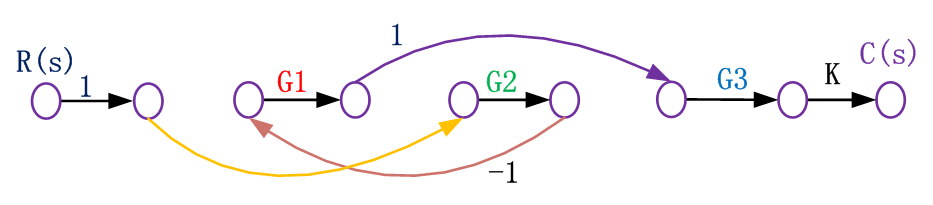
把系統結構圖轉換為信號流圖：

在系統結構圖的信號線上，用小圓圈標注各變量對應的節點

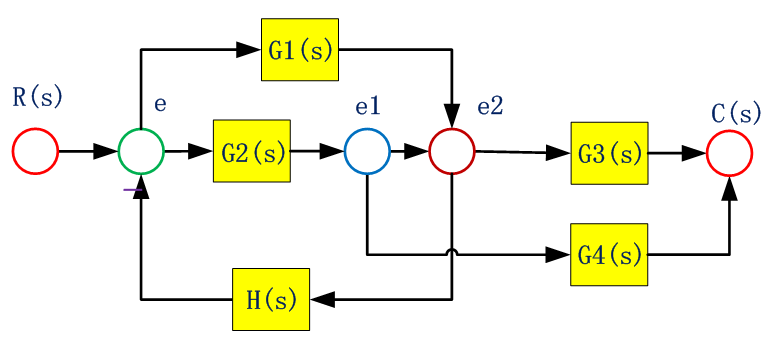
將各節點按原來順序自左向右排列，把方框用帶有增益的支路代替

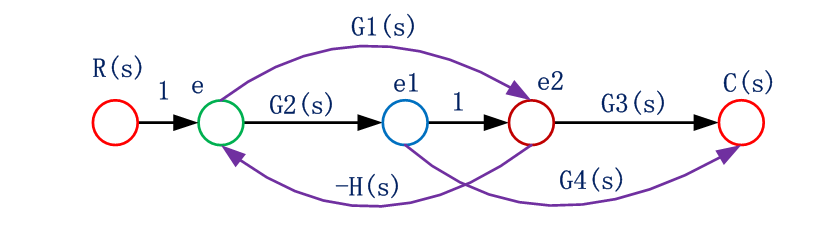
系統存在2個單獨回路G2H,G1H，3個前向通道G1G3,G2G3,G2G4。不接觸回路為零。

從源節點R到阱節點C的前向通道共有3條，前向通道總增益及余因子式分別為：

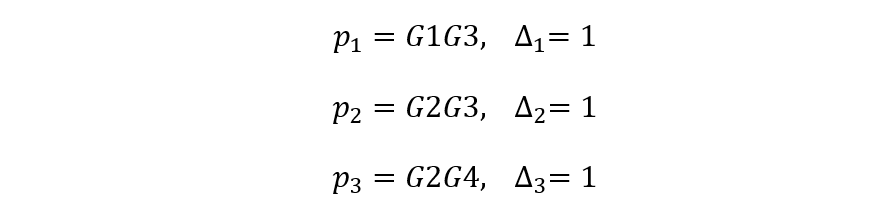
單獨回路有2個：

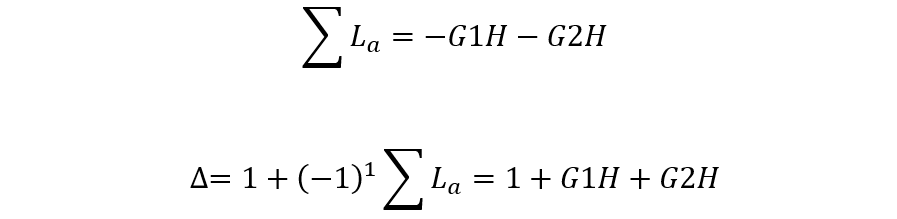
獲得系統傳遞函數：

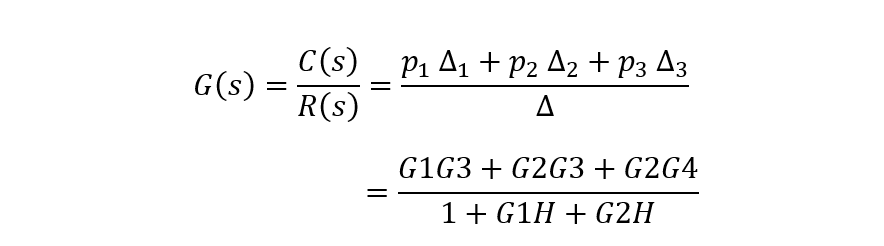
可見，運用梅森公式可以非常方便的計算系統傳遞函數，省去了結構圖的簡化過程。