顯著加快多項式運算速度
幾乎任何代數計算最終都會以某種方式涉及多項式。多項式從一開始就是Mathematica 和Wolfram語言中優化的部分。事實上,在超過四分之一個世紀的時間里,我們對它們進行的基本操作幾乎不需要更新。但是現在在版本13.2中——由于新的算法和新的數據結構,以及使用現代計算機硬件的新方法——我們正在更新一些核心多項式運算,并使它們大大加快。順便說一下,我們也得到了一些新的多項式函數。
這是兩個多項式的乘積,展開:
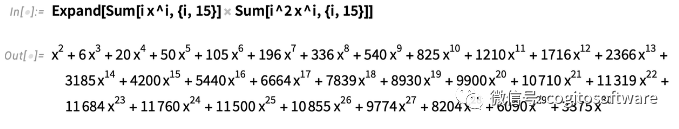
像這樣的分解多項式幾乎是即時的,并且從版本1 開始就一直如此:
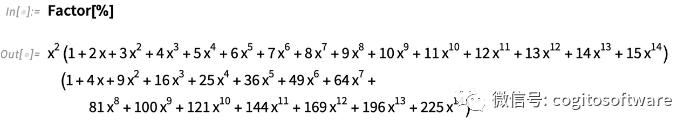
但是現在讓我們把它做得更大:
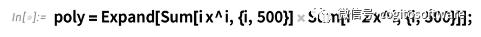
展開多項式中有999 項:

分解這不是一個簡單的計算,在版本13.1 中大約需要19 秒:

但是現在,在版本13.2 中,同樣的計算需要0.3 秒,快了近60 倍:
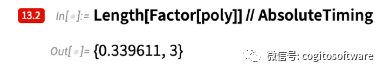
很少有任何東西能提高60倍。但這是其中一種情況,事實上,對于更大的多項式,該比率將進一步穩步增加。但這僅僅是只與晦澀的大多項式有關的東西嗎?嗯,沒有。尤其是因為事實證明,大多項式出現在各種重要地方的“引擎蓋下”。例如,看似無害的物體
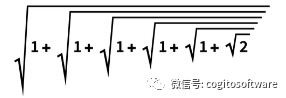
可以作為代數數進行操作,但多項式最小:
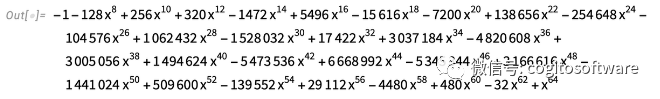
除了分解之外,版本13.2還顯著提高了多項式結果、GCD、判別式等的效率。所有這些都使得對多項式線性代數的變革性更新成為可能,即對元素為(單變量)多項式的矩陣的操作。
下面是一個多項式矩陣:
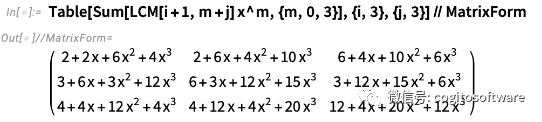
這是矩陣的力量:
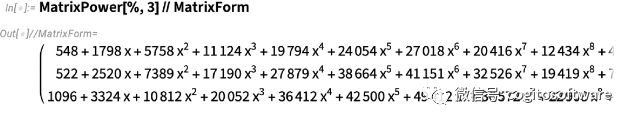
而這個的決定因素:
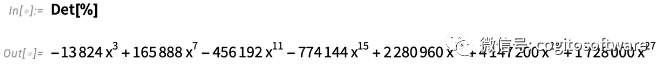
在13.1 版中,這看起來并不那么好;結果未展開,如下所示:
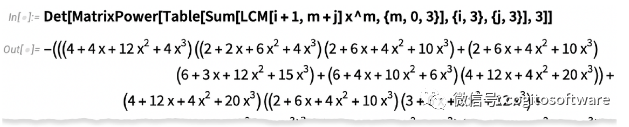
在版本13.2 中,大小和速度都得到了顯著改進。這是一個更大的案例- 在 13.1中計算需要一個多小時,結果的葉子數量驚人地達到178 億


多項式線性代數在“幕后”用于許多領域,特別是在處理線性微分方程、差分方程及其符號解時。在13.2版本中,不僅多項式MatrixPower和Det,而且LinearSolve,Inverse,RowReduce,MatrixRank和NullSpace都得到了顯著的加速。
除了顯著的速度改進之外,版本13.2 還增加了一個多項式功能,我碰巧已經等待了30 多年:有限域上的多元多項式分解:
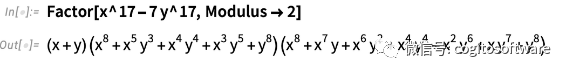
事實上,查看我們的檔案,我發現許多請求至少可以追溯到1990 年——來自相當多的人——要求這種能力,盡管1991 年的內部說明很有魅力地指出:

是的,沒錯。但是31 年后,在13.2 版中,它完成了!
審核編輯 :李倩
-
Wolfram
+關注
關注
0文章
16瀏覽量
7765 -
函數
+關注
關注
3文章
4359瀏覽量
63530 -
數據結構
+關注
關注
3文章
573瀏覽量
40417
原文標題:Wolfram語言與Mathematica 13.2 版本(4)
文章出處:【微信號:哲想軟件,微信公眾號:哲想軟件】歡迎添加關注!文章轉載請注明出處。
發布評論請先 登錄
相關推薦
新品 | Module LLM Kit,離線大語言模型推理模塊套裝

了解DeepSeek-V3 和 DeepSeek-R1兩個大模型的不同定位和應用選擇
gitee 支持的編程語言有哪些
如何優化 Mathematica 代碼性能
Mathematica 在數據分析中的應用
特斯拉FSD V13.2版本正式發布
特斯拉發布“完全自動駕駛”軟件最新版本FSDV13.2
USB4 2.0版本的重大更新
PwrCAN Module 13.2 | 雙CAN通道+RS485通信,隔離電源,多場景通信專家

X-CUBE-CRYPTOLIB V4庫文件無法添加,鏈接錯誤的原因?
iOS版ChatGPT支持首選語言設置中文
商湯將發布日日新大模型5.0粵語版本
樹莓派5最大的競爭對手OrangePi 5 Pro?,新增4GB/8GB版本



















評論