前言：如果說要在16bit定點環境上使用DSP算法，如IIR構成的2P2Z，會受到定點編程和量化精度的問題。如果說在float32環境上可以很容易進行編程，那切換到定點環境上就不得不得考慮這些問題。通常情況下單精度浮點在小數點后的精度為1/（2^23），理論上使用32位定點IQ24就可以覆蓋單精度浮點的精度問題，但是在16bit上，使用i1.q15的方法來算，僅有1/(2^15)的精度，如果直接使用則會遇到量化精度引起的誤差問題。那么該如何把浮點切換到16bit的定點來呢，下面將一步一步的來進行討論。

S1 傳遞函數離散

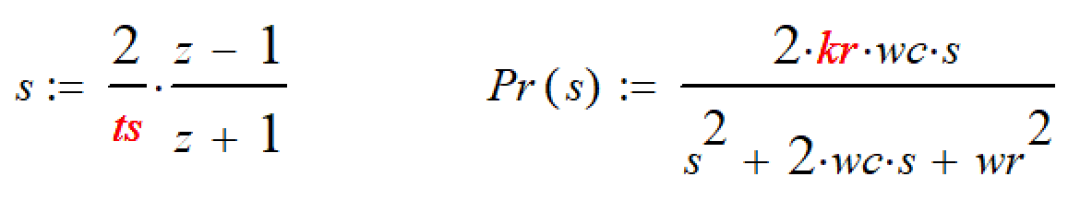
離散化：

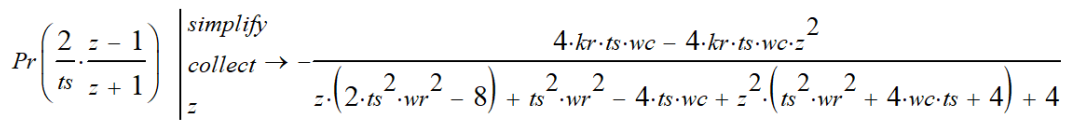
帶入參數，并出歸一化的z域傳遞函數，這里把分母的z^2提出來，然后全部除以其它的數字，即可得到：

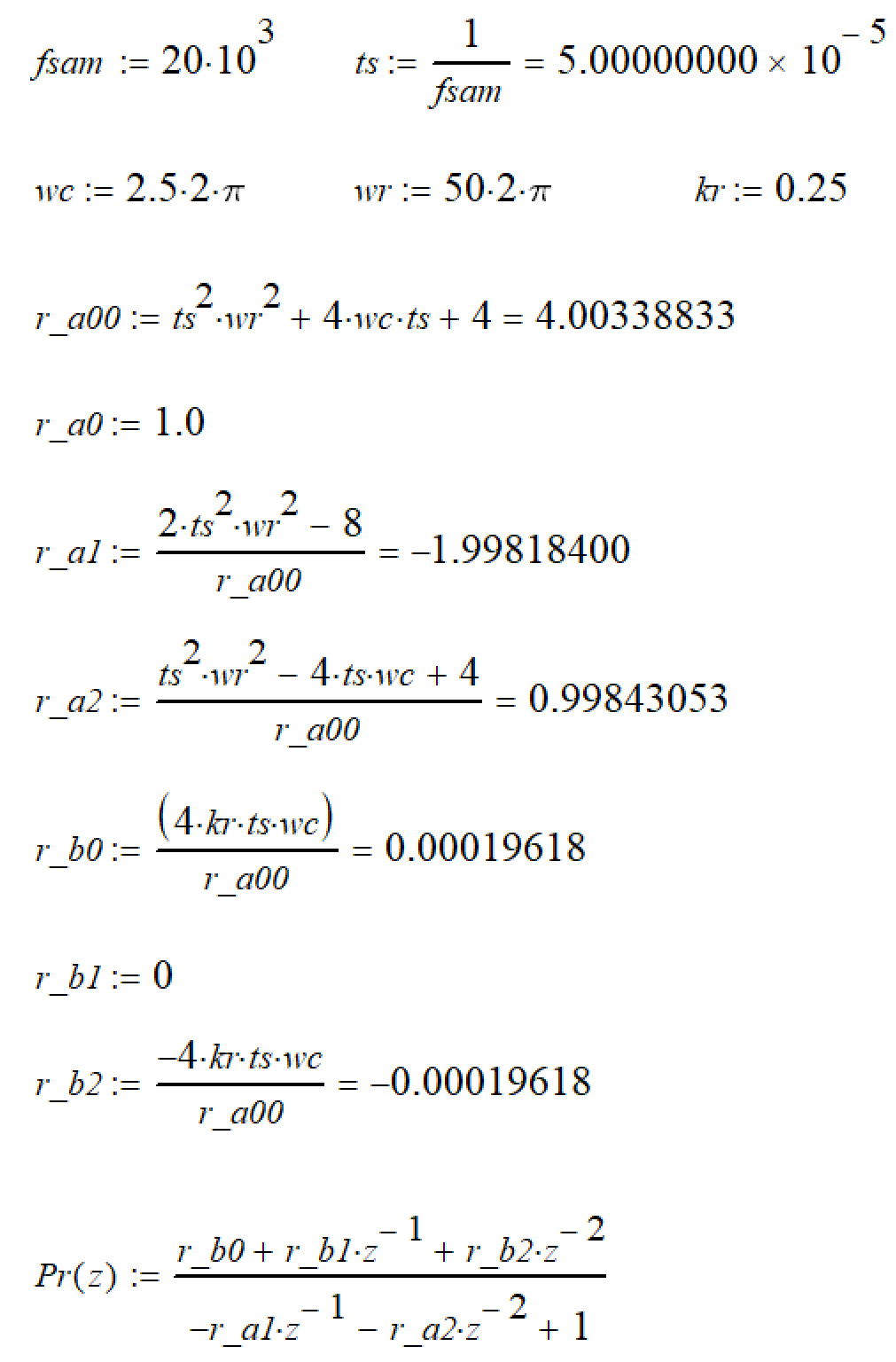
S2 使用IQ15的方法量化：

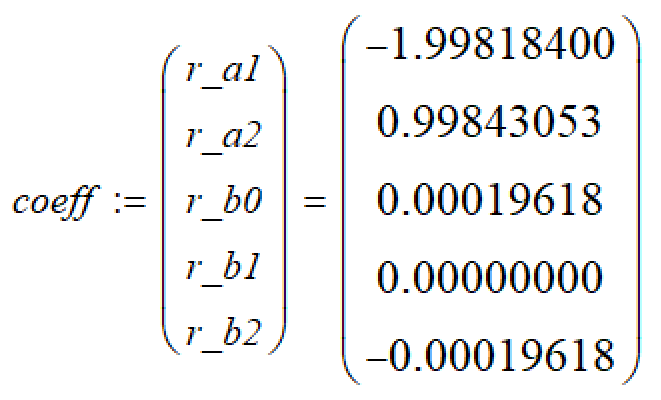
可見，a1項為最大，即可把全部數字除以a1項，讓它用滿15bit的字長，可得：

然后乘以2^15，得到：

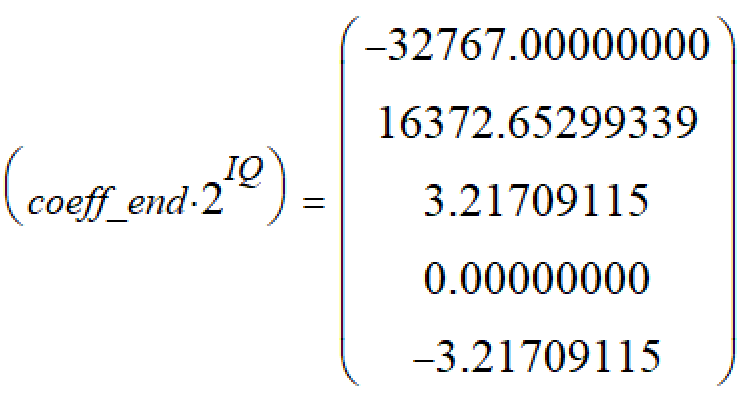
S3 提升B系數：這里可以看到分子項上B0/B2的數字太小，所以為了提高量化精度，可以在B系數上繼續擴大到2^12，這樣可以更多的利用字長，最后在輸出上除去引入增益即可。

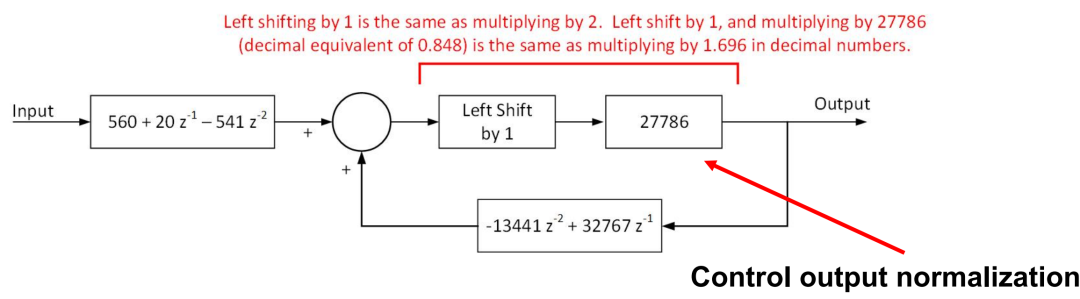
可得B系數更新為。

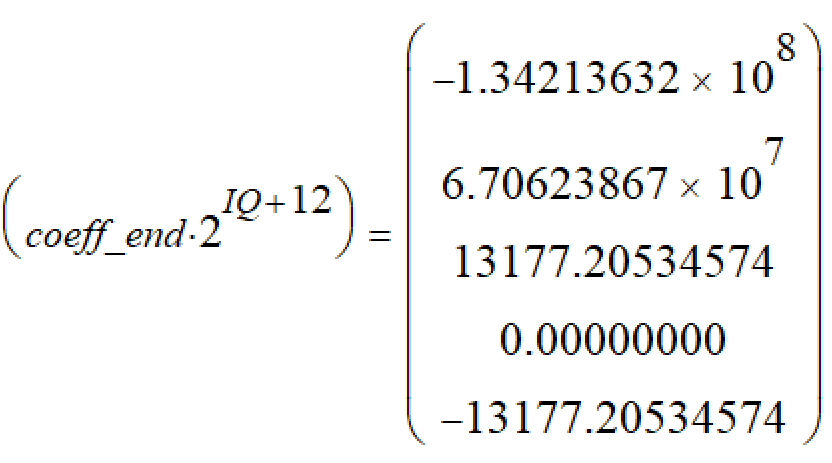
然后考慮一下分母量化為32786時引入的增益：1.99998，在編程上考慮先左移1位然后再考慮小數點（32709/32678）即可引入增益。然后開始測試定點化后的PR控制器：

S4 測試：輸入測試信號為50hz正弦波：

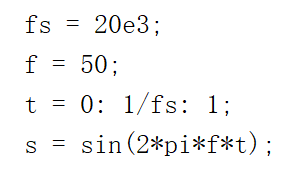
run，這里使用floor函數，進行向下取整來進行定點化：

S5 輸出：可見定點和浮點的輸出波形幾乎接近，存在很小的誤差，屬于可以接受的量化精度。

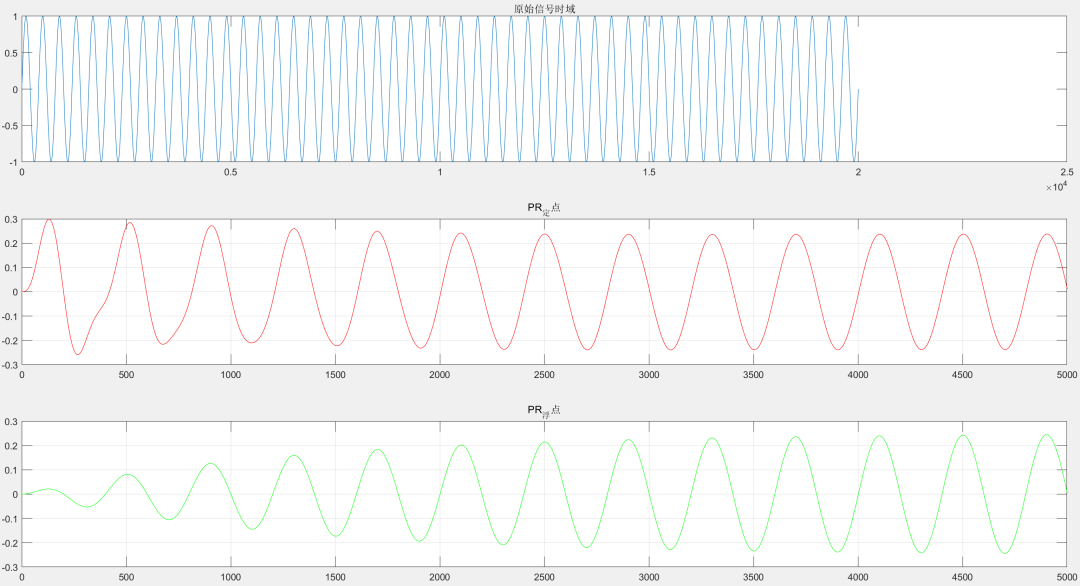
小結：可見在充分利用上32768的精度后，PR控制器很好的運行在16bit環境上，如果是32bit的定點環境，則無需這么麻煩，直接使用I6Q24即可達到單精度浮點的精度。本人能力有限，如果錯誤懇請幫忙指正，謝謝觀看。