根據牛頓定律，運動物體總是有趨于靜止，或保持運動的特性，我們把物體所具有的這種狀態，叫做穩態，與此相反的非穩態，叫做瞬態，瞬態是反應物體變化過程的模型。

在數字電路設計中，到達0或1這兩種穩態的過程，實際上是連續的，而我們把它當做是離散信號，一個離散信號，可以看做是一個連續信號在跳變瞬間的時間增量為無窮小，即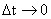：，通常我們不考慮這個連續過程，但在產品的穩定性和可靠性設計上，必須要考慮這個問題，即離散信號的連續特性，或者說瞬態。

設某一精密電源，其額定輸出為24V240w，考慮到，上電瞬間對母電源的沖擊，引起其它單元模塊的電壓波動，我們需要適當限制其瞬間沖擊功率，待到電路基本穩定時，再馬力全開。

設某一RC電路，如下圖所示。

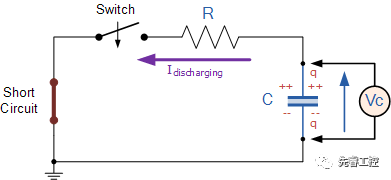
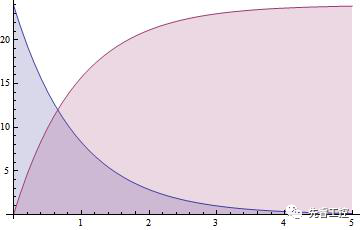
在該電路中，由電壓模型，我們得知：

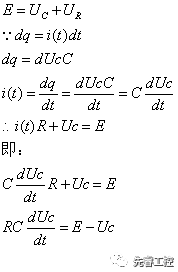
解此微分方程：

解，設，當電源電壓為24V，電阻為100歐姆，電容為4700uf X2 則，代入上式，得電壓與時間的函數關系如下圖所示。

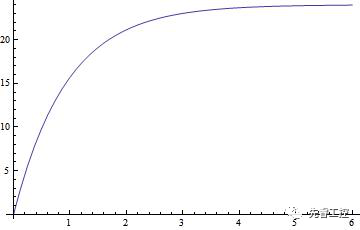
設，設計某一電路，當電容充電至18伏時，全功率開啟，則t=?

即，在上電之后 ，經過1.3秒時間，電壓上升至18伏。

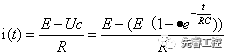
將以上解代入原式，得電流與時間的函數關系如下圖所示。

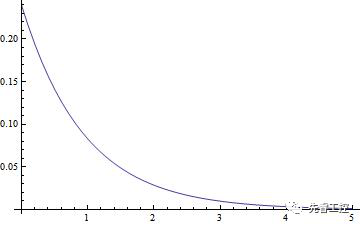
當我們把電流放大100倍時，函數關系如上。

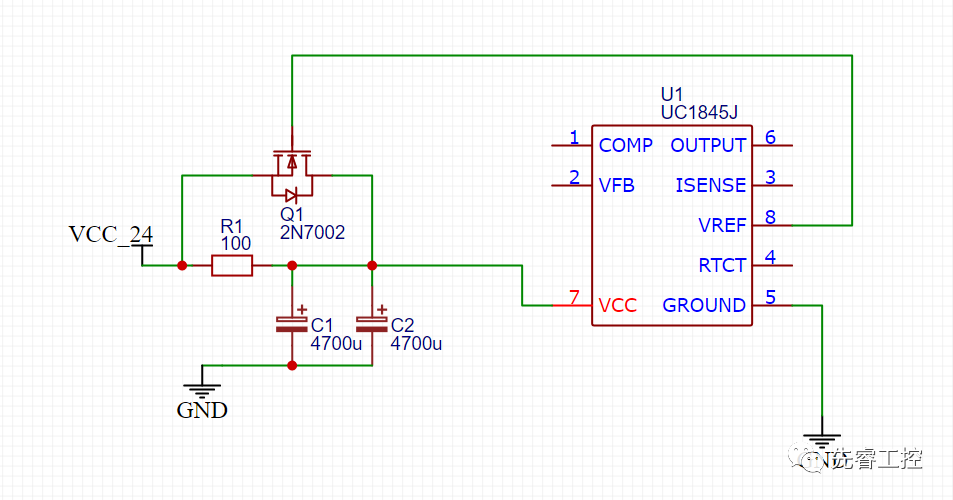
根據上述方程的解，當我們設計一個電源，如下圖所示，確定合適的R1,C1,C2的值，就可以起到防沖擊作用，反之，大容量電容所引起的瞬間沖擊是不容小窺的事。

先睿工控：恭祝大家新春愉快，萬事如意，闔家歡樂！