前兩期介紹了Clarke的Park變化的基本原理，但是經(jīng)過這兩種變換后會(huì)存在兩種系數(shù)，相信大家都很迷惑，這是什么原因? 主要原因是存在兩種遵循的方式：1、變換前后電流所產(chǎn)生的旋轉(zhuǎn)磁場等效且電機(jī)輸出功率不變; 2、變換前后電流所合成的空間矢量等效且電機(jī)輸出功率不變。 這兩種最后方式是造成系數(shù)不同的根本原因，實(shí)際應(yīng)用中可以根據(jù)需要選擇相應(yīng)的變換等效原則。

關(guān)鍵詞：旋轉(zhuǎn)磁場等效; 空間矢量等效;

這一期設(shè)計(jì)的理論計(jì)算能力比較強(qiáng)，強(qiáng)烈建議觀看的小伙伴找個(gè)安靜的角落，哪張紙和筆進(jìn)行計(jì)算!

01依據(jù)旋轉(zhuǎn)磁場等效變換

遵循的兩個(gè)原則：

a、變換前后電流所產(chǎn)生的旋轉(zhuǎn)磁場等效;

b、變換前后兩系統(tǒng)的電機(jī)輸出功率不變;

1.1、Clarke變換

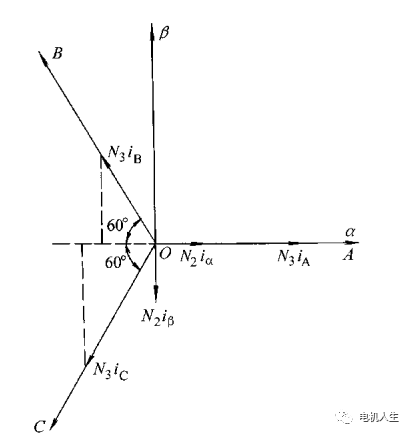
圖1-1是ABC和αβ兩個(gè)坐標(biāo)系，取α軸與A軸重合，并假定三相繞組每相有效線圈匝數(shù)為N3，兩相繞組每相有效線圈匝數(shù)為N2，兩種坐標(biāo)系中每相的磁動(dòng)勢均為有效線圈匝數(shù)與該相電流的乘積。

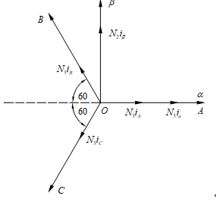
圖1-1 Clarke坐標(biāo)變換矢量示意圖1

由圖1-1得出磁勢守恒式子為：

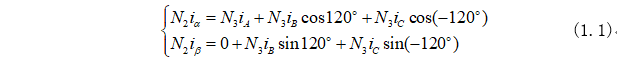
由式(1.1)變形化為矩陣形式為：

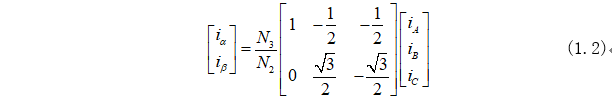
為了方便分析，引入零軸變量為：

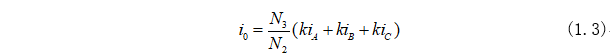
將式(1.3)合并到式(1.2)可以得到αβ0軸坐標(biāo)系方程為：

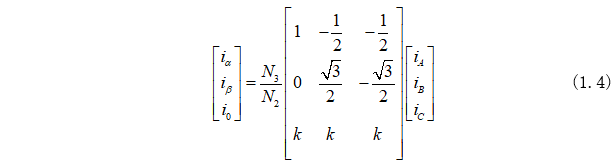
這里定義Clarke矩陣為：

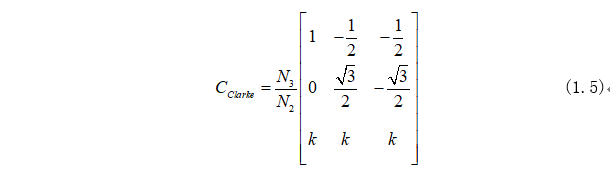
坐標(biāo)變換中需要確保電機(jī)輸出功率不能發(fā)生變化，故功率計(jì)算表達(dá)式為：

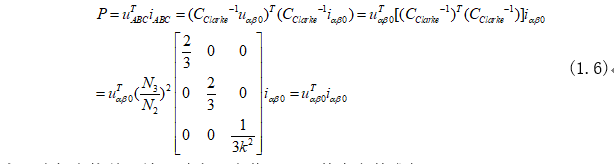
為了確保變換前后輸出功率不變化，可以其中參數(shù)求得：

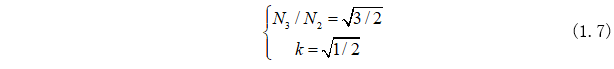
因此Clarke變換式為：

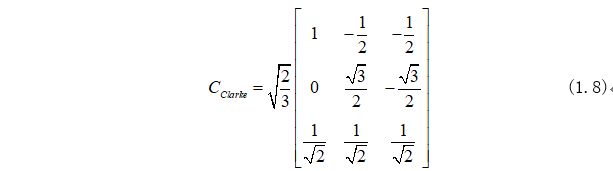
1.2、Park變換

圖1-2是兩相旋轉(zhuǎn)坐標(biāo)系轉(zhuǎn)速w隨著電機(jī)轉(zhuǎn)子轉(zhuǎn)動(dòng)，αβ是兩相靜止坐標(biāo)系，dq是兩相旋轉(zhuǎn)坐標(biāo)系。

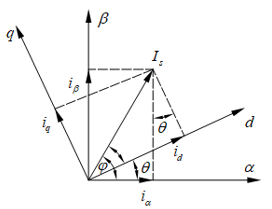
圖1-2 Park坐標(biāo)變換示意圖1

由第二期內(nèi)容可知，Park變換式為：

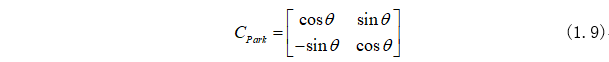
1.3、功率計(jì)算

電機(jī)功率可以計(jì)算為：

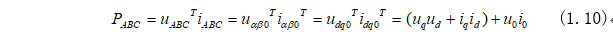
02依據(jù)空間矢量等效變換

遵循的兩個(gè)原則：

a、變換前后電流所合成的空間矢量等效;

b、變換前后兩系統(tǒng)的電機(jī)輸出功率不變;

2.1、Clarke變換

圖2-1中空間矢量Is在αβ軸上的投影分別為ia、iβ，且與A軸夾角為φ。

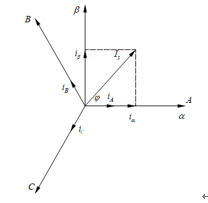
圖2-1 Clarke坐標(biāo)變換矢量示意圖2

根據(jù)圖2-1所示可以得到三相電流與空間矢量Is關(guān)系式為：

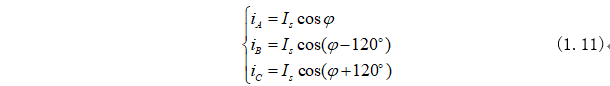
同理可以得到兩相靜止坐標(biāo)系中電流ia、iβ與空間矢量Is關(guān)系式為：

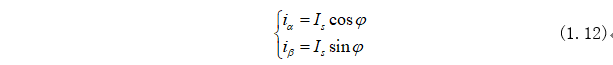
根據(jù)三角恒等式：

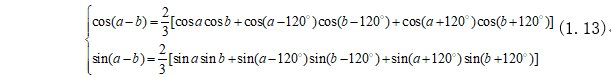
根據(jù)三角恒等式(1.13)將式(1.12)變化為：

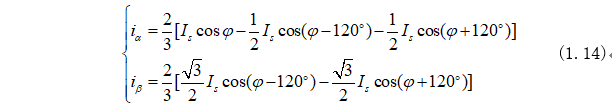
寫成矩陣形式為：

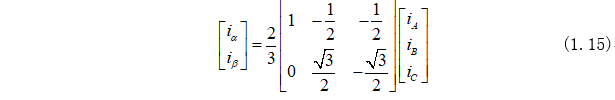
同樣，引入零軸變量：

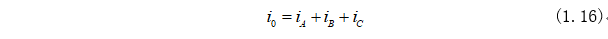
將式(1.16)代入式(1.15)中可以得到新的矩陣形式為：

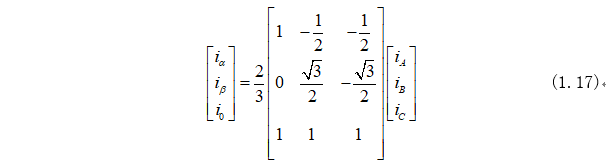
那么Clarke變換矩陣為：

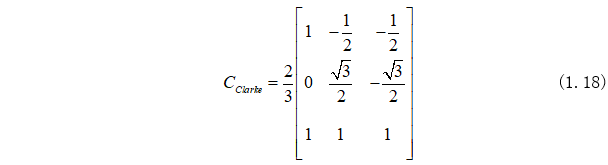
2.2、Park變換

同樣，圖2-2是兩相旋轉(zhuǎn)坐標(biāo)系轉(zhuǎn)速w隨著電機(jī)轉(zhuǎn)子轉(zhuǎn)動(dòng)，αβ是兩相靜止坐標(biāo)系，dq是兩相旋轉(zhuǎn)坐標(biāo)系。

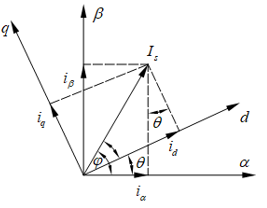
圖2-2 Park坐標(biāo)變換示意圖2

由第二期內(nèi)容可知，Park變換式為：

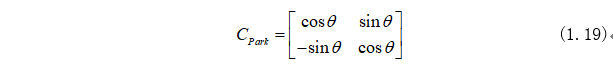
2.3、功率計(jì)算

電機(jī)功率可以計(jì)算為：

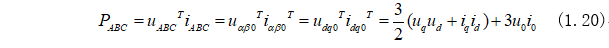
03總結(jié)

由磁動(dòng)勢守恒計(jì)算出的電機(jī)功率為：

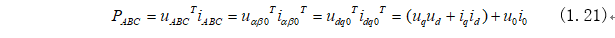
由空間矢量守恒計(jì)算出的電機(jī)功率為：

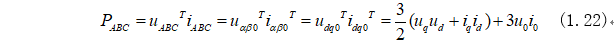
兩種變換存在一個(gè)3/2的系數(shù)區(qū)別，主要是各自采用了不同的變換形式，最后得出的功率都是對的!