在分析時域電路中,對于電容和電感這兩個儲能元件,往往要考慮換路前后的狀態值,才能用公式進行求解,這種電路就是動態電路,對于電路中只有一個電感或者電容的電路可以用一階線性微分方程進行分析。
關鍵詞:動態電路;電容;電感;
01動態電路的分析方法
1.1、n階微分方程電路的由來
在一般情況下,當電路中僅含有一個動態元件,動態元件以外的線性電阻電路可用戴維寧定理或者諾頓定理置換為電壓源和電阻的串聯組合,或電流源和電阻的并聯組合,對于這樣的電路,所建立的電路方程將是一階線性常微分方程,相應的電路稱為一階電路。當電路中含有兩個或n個動態元件時,建立的方程為二階微分方程或n階微分方程。
1.2、動態電路的分析方法
什么是過渡過程?
含有動態元件的電路又稱為電路,動態電路的一個特征是當電路的結構或元件的參數發生變化時(例如電路中電源或無源元件的斷開或接入,信號的突然注入等),可能使電路改變原來的工作狀態,轉變到另一個工作狀態,這種狀態往往需要經歷一個過程,在工程上稱為過渡過程。
什么是換路時刻?
上述電路結構或者參數變化引起的電路變化統稱為“換路”,并認為換路是在t=0時刻進行的。為了敘述方便,把換路前的最終時刻記為t=0-,把換路后的最初時刻記為t=0+,換路經歷的時間為0-到0+。
采用什么樣的分析方法?
分析動態電路的過渡過程的方法之一就是:根據KCL、KVL和支路的VCR建立描述電路的方程,這類方程是以時間為自變量的線性常微分方程,然后求解常微分方程,從而得到電路所求變量(電壓或電流)。這方法稱為經典法,它是一種在時間域中進行的分析方法。
使用經典法需要注意的事項?
使用經典法求解常微分方程時,必須根據電路的初始條件確定解答中的積分常數,設描述電路動態過程中的微分方程為n階,所謂初始條件就是指電路中所求變量(電壓或電流)及其1階至(n-1)階導數在t=0+時的值,也稱為初始值。電容電壓Uc(0+)和電感電流iL(0+)稱為獨立的初始條件,其余的稱為非獨立的初始條件。
02電容和電感動態分析
2.1、電容分析
對于【線性電容】,在任意時刻t內,它的電荷q、電壓u和電流i的關系為:
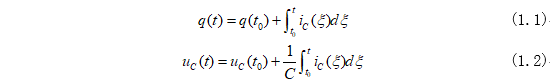
式(1.1)和式(1.2)表明電容的電荷量和電壓不會突變,是一個隨時間積累的量。用0-和0+表示,即為:
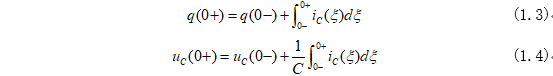
式(1.3)和式(1.4)表明電容在換路前后,電流ic為有限值,換路瞬間積分項會為0,但是電容和電荷不會發生躍變,變化即滿足:
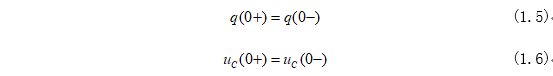
2.2、電感分析
對于【線性電感】,在任意時刻t內,它的磁通鏈、電壓u和電流i的關系為:
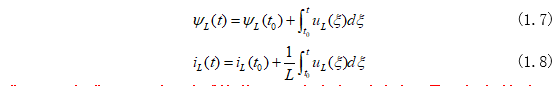
式(1.7)和式(1.8)表明電感的磁通量量和電流不會突變,是一個隨時間積累的量。用0-和0+表示,即為:
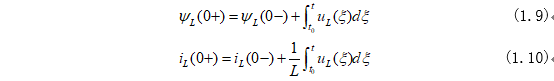
式(1.9)和式(1.10)表明電感在換路前后,電壓uc為有限值,換路瞬間積分項會為0,但是電流和磁通量不會發生躍變,變化即滿足:
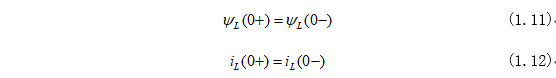
式(1.11)和式(1.12)表明電感在換路瞬間,電感可以視為一個電流為i(0)的電流源,對于一個t=0時電流為零的電感,在換路瞬間,有i(0)=0,所以換路瞬間電感相當于斷路。
-
電容
+關注
關注
100文章
6133瀏覽量
152227 -
電感
+關注
關注
54文章
6170瀏覽量
103181 -
動態電路
+關注
關注
1文章
27瀏覽量
9635 -
動態分析
+關注
關注
1文章
19瀏覽量
7309 -
時域電路
+關注
關注
0文章
2瀏覽量
4349
發布評論請先 登錄
相關推薦
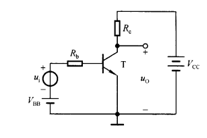
基本共射放大電路的組成、靜態分析及動態分析
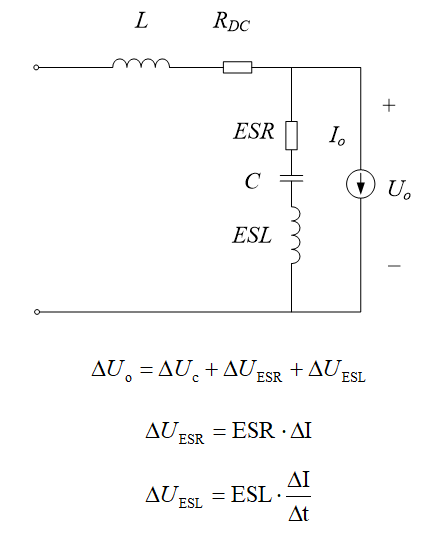
Buck電路動態響應影響因素分析
空間動態模型建模方法分析
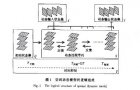
基于對象跟蹤的動態分析方法
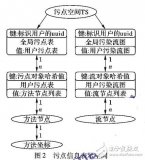
物理老師告訴你電路的動態分析方法及注意要點
共基極放大電路的動態分析步驟


















評論