了解積分非線性 （INL） 規范及其與模數轉換器 （ADC） 誤差的關系。

失調誤差、增益誤差和INL這三個參數決定了ADC的精度。失調和增益誤差可以校準出來，這使得INL成為主要的誤差貢獻者。INL規范描述了實際傳遞函數的過渡點與理想值的偏差。

什么是積分非線性 （INL）？

理想的ADC具有均勻的階梯輸入-輸出特性，這意味著每次轉換發生在與上一個轉換相距1 LSB（最低有效位）處。但是，對于實際ADC，步驟并不統一。例如，考慮圖1所示的傳遞曲線。

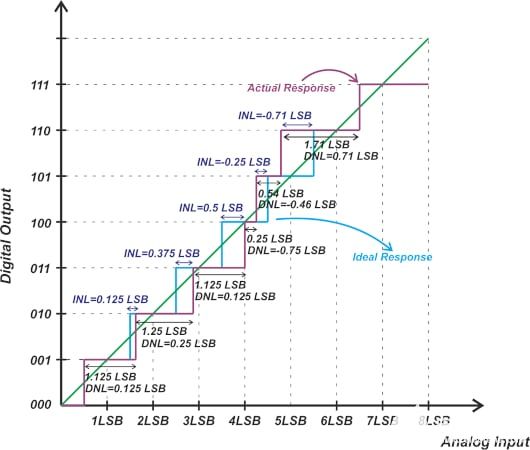
圖1. ADC的傳輸曲線示例。

步寬與理想值的偏差由微分非線性（DNL）規范表征。然而，DNL誤差不能完全描述傳遞函數與理想響應的偏差，因為我們獲得的響應取決于DNL正負誤差在不同代碼中的分布方式。INL 規范允許我們表征代碼轉換與其理想值的偏差。要計算代碼 k 的 INL，我們可以使用以下等式：

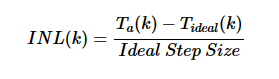
其中 T一個（k）和T理想（k） 分別表示從代碼 k-1 到 k 的實際和理想過渡;“理想步長”是ADC的LSB。對于上述示例，從代碼 1 （001） 到代碼 2 （010） 的實際轉換發生在理想轉換上方 0.125 LSB 處。因此，代碼 2 的 INL 是 INL（2） = +0.125 LSB。

從這里開始，我們可能會問，下一個轉換（從代碼 2 到 3）呢？請注意，從代碼 1 到 2 的轉換發生在理想值以上 0.125 LSB 處，并考慮到代碼 2 的寬度誤差（或 DNL）為 +0.25 LSB，我們可以推斷從代碼 2 到 3 的轉換應該發生在理想值以上 0.375 LSB 處。因此，我們有 INL（3） = +0.375 LSB。如您所見，代碼 3 的 INL 等于代碼 1 和 2 的 DNL 之和：

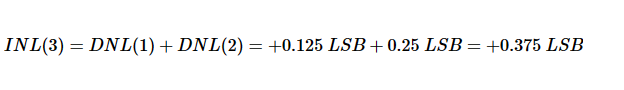
將上述分析擴展到其他代碼，很容易通過應用以下等式來驗證第 m 個代碼的 INL：

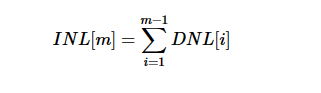
INL 表示 DNL 錯誤的累積影響。在計算DNL和INL值時，我們假設ADC的失調和增益誤差已經校準出來。因此，第一個代碼（代碼 1）和最后一個代碼的 INL 為零。對于代碼零，未定義 INL。

表示 ADC INL 信息

就像 DNL 一樣，我們可以將 INL 信息表示為 INL 相對于代碼值的圖。對于上面的示例，我們得到如圖 2 所示的下圖。

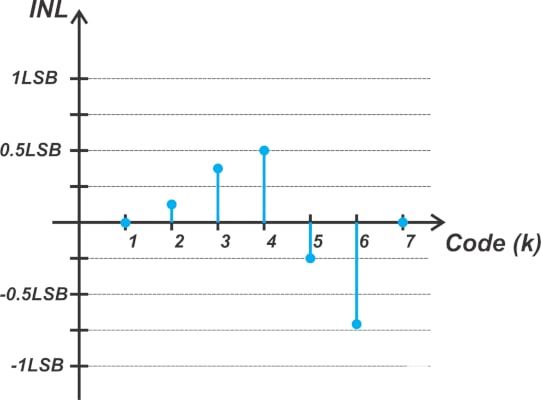
圖2. 顯示 INL 相對于代碼值的示例圖。

INL 通常也表示為所有代碼的最小值和最大值。我們假設的ADC的INL介于-0.71 LSB和+0.5 LSB之間。INL圖不僅表示ADC的線性度性能，而且還揭示了有關ADC內部架構的一些信息。例如，子范圍ADC具有三角形INL圖（圖3（a）），而閃存ADC通常具有隨機模式（圖3（b））。

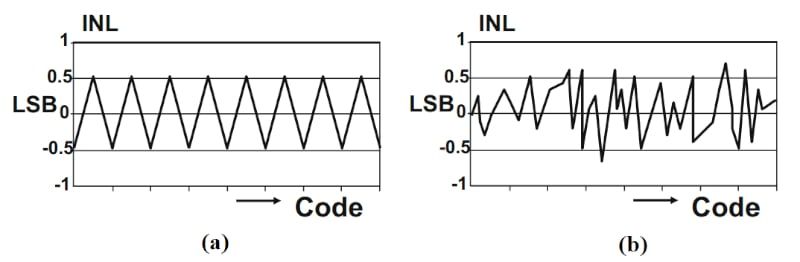
圖3.子范圍ADC三角形INL圖（a）和閃存ADC的隨機模式圖（b）示例。圖片由 M. Pelgrom 提供

INL：超出ADC量化誤差的誤差

需要注意的是，INL除了指定ADC的量化誤差外，還指定了一個誤差。由于ADC將連續模擬輸入范圍轉換為多個離散輸出代碼，因此即使是理想的ADC也會固有地會在系統中引入一些誤差，稱為量化誤差。如果我們將斜率為1的斜坡輸入施加到ADC，則可以從輸入中減去輸出代碼的模擬等效值，以找到量化誤差。如圖 4 所示。

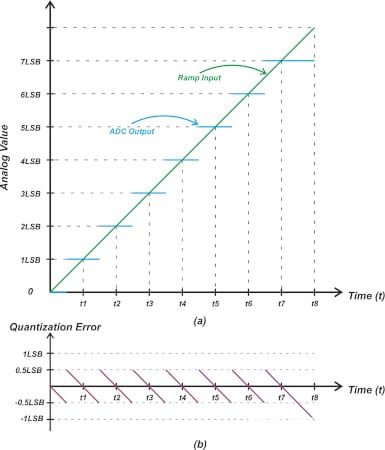
圖4. 顯示量化誤差的示例圖。

在圖4中，綠色曲線表示斜坡輸入，藍色階躍表示理想ADC產生的代碼的模擬等效值。然而，圖4中的下圖顯示了鋸齒形狀的量化誤差。讓我們看看非線性如何影響誤差項。如果將斜坡輸入應用于圖1中的非理想特性曲線，則得到以下誤差波形（圖5）。

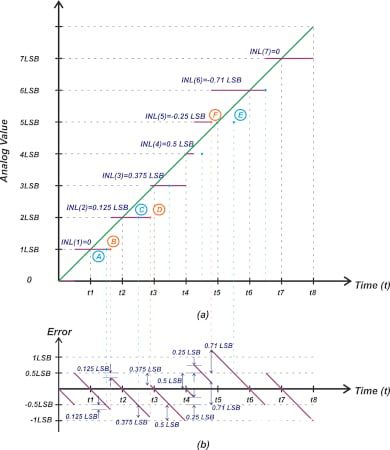
圖5. 示例圖顯示了ADC輸出代碼的模擬等效值以及理想變換（a）和誤差波形（b）。

圖5（a）中的紫色階躍表示ADC輸出代碼的模擬等效值，藍點表示均勻階梯響應的理想過渡點。例如，考慮從代碼 1 到代碼 2 的轉換。如果這種轉換發生在理想點（A點），則代碼1的最負誤差將是-0.5 LSB。由于 INL（2）=+0.125 LSB，因此從代碼 1 到代碼 2 的實際轉換發生在高于理想值的 +0.125 LSB 處。由于這種延遲轉換，綠色曲線與ADC輸出之間的差值在轉換點（B點）大于0.5 LSB。通過檢查該圖，您可以確認 B 點的誤差由下式給出：

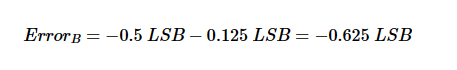
請注意，雖然這種非理想效應將代碼 1 的誤差擴展到 -0.625 LSB，但它將下一個代碼（代碼 2）的誤差上限降低到 0.5 LSB - 0.125 LSB = +0.375 LSB。您可以在 D 點看到由 INL（3） = +0.375 LSB 引起的誤差波形的類似變化。

讓我們檢查代碼 6，看看負 INL 如何影響錯誤 （INL（6 ）= -0.71 LSB）。在這種情況下，（F點）處的實際躍遷發生在理想值（E點）以下0.71 LSB處。由于ADC輸出增量早于預期值，因此會產生較大的正誤差。如錯誤圖所示，代碼 6 的誤差可以大到：

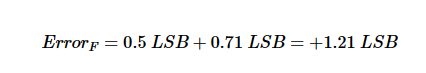
使用理想ADC時，量化過程會產生±0.5 LSB的誤差。然而，對于實際的ADC，量化過程和INL都會影響系統的整體誤差。換句話說，INL是超出量化誤差的誤差。

到目前為止，我們考慮的INL定義可能是該規范中最有用和最常見的定義。但是，應該注意的是，ADC制造商的教科書和技術文檔中有時會提到其他一些定義。為了避免任何混淆，我們將在本文的其余部分查看INL的其他常見定義。

重新定義INL代碼：不同但相同的定義

在我們繼續其他定義之前，值得一提的是，人們可以用稍微不同的方式查看圖 1 中使用的定義。與其將 INL 定義為代碼轉換與其理想值的偏差，我們可以將其定義為代碼轉換與經歷第一個和最后一個代碼轉換的直線的偏差。如圖 6 所示。

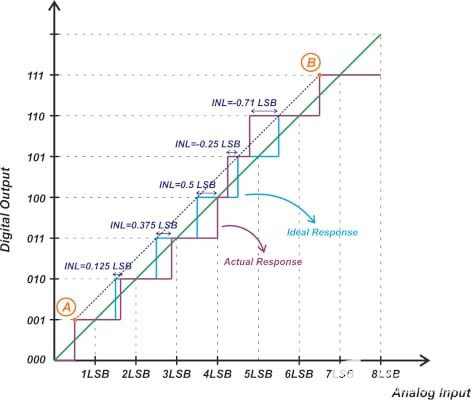
圖6. 顯示代碼在實際響應和理想響應之間的偏差的圖。

在圖 6 中，點 A 和 B 是第一個和最后一個轉換點。由于我們假設在INL計算之前失調和增益誤差為零，因此A點和B點對應于理想和實際傳遞函數。如您所見，穿過點 A 和 B 的線也穿過理想特性的所有其他過渡點（圖中的藍色曲線）。因此，實際過渡點與其相應理想過渡點的偏差等于該實際過渡點與穿過點 A 和 B 的直線的偏差。一些參考文獻，如《高速模數轉換》一書，使用此直線來定義ADC INL。另請注意，此參考線與之前文章中介紹的ADC線性模型（圖中的綠線）不同。

定義 INL - 代碼中心行定義

對于這種類型的定義，ADC傳輸特性是根據穿過ADC代碼中心的直線定義的。圖 7 顯示了如何使用代碼中心線定義 INL。

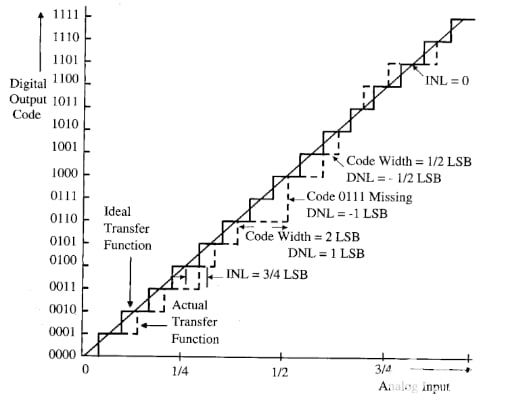
圖7.使用代碼中心線定義 INL。圖片由 R. Plassche 提供

在上面的示例中，對角線是穿過理想ADC階躍中點的線（我們在本系列的文章中稱之為ADC的線性模型）。如圖所示，實際步長中點與直線的偏差被視為該代碼的INL誤差。

此示例顯示了此定義的一個缺點。如您所見，代碼 1101 的相鄰轉換偏離了理想值。但是，由于 1101 的測量代碼中心與理想值一致，因此該代碼的 INL 為零。使用圖 1 中使用的定義，代碼 1101 的 INL 將不為零。

作為旁注，上面的圖片取自Rudy van de Plassche的書。Rudy是世界著名的模擬設計師和許多電路和電路創意的發明者，例如斬波和穩定放大器，這些電路和電路理念在今天被廣泛使用。

另一個基于代碼中心的定義如圖 8 所示。

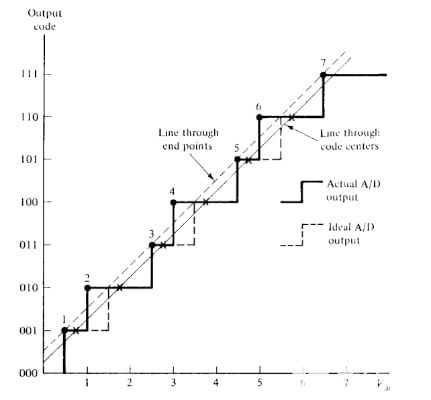
圖8.顯示代碼中心行定義的示例圖。圖片由M. Demler提供

在這種情況下，用于計算INL誤差的參考線是穿過實際傳遞函數的第一個和最后一個步驟的中點的線。對于三位ADC，這是穿過代碼001和110中點的線路。實際步長的中點與這條直線的偏差被認為是該代碼的INL誤差。

在這個特定的例子中，ADC傳遞函數具有交替的寬窄代碼，從第一個和最后一個代碼獲得的參考線截獲所有代碼的中點。因此，所有代碼的 INL 錯誤均為零。這再次凸顯了基于代碼中心的定義在某些情況下無法描述傳遞函數的非線性的缺點。

本文中討論的 INL 定義被歸類為基于端點的定義，因為它們僅使用第一個和最后一個代碼來派生參考線。定義 INL 誤差的另一種方法是最佳擬合方法。在這種情況下，使用一條適合所有代碼的直線作為參考線。本系列的下一篇文章將詳細研究最佳擬合方法。