本文介紹開發(fā)組合邏輯電路時可能發(fā)生的意外開關(guān)事件,稱為危險。
本文是關(guān)于使用邏輯門進行組合電路設(shè)計和仿真的介紹性系列文章的第二部分。在上一篇文章中,我們介紹了 組合邏輯電路 以及如何簡化它們。
在這里,我們將探討靜態(tài) 0 危害、靜態(tài) 1 危害和動態(tài)危害。
什么是邏輯危險?
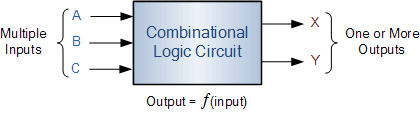
在復(fù)雜的邏輯電路中,輸出端可能會出現(xiàn)不需要的臨時開關(guān)事件。圖1顯示了組合邏輯電路中可能發(fā)生的三種危險:
靜態(tài) 0 危險: 輸出在本應(yīng)保持 0 時暫時更改為 1
靜態(tài) 1 種危險: 輸出在本應(yīng)保持 1 時暫時更改為 0
動態(tài)危險: 輸出在應(yīng)該進行單個邏輯轉(zhuǎn)換時會多次更改;從 0 到 1 或從 1 到 0
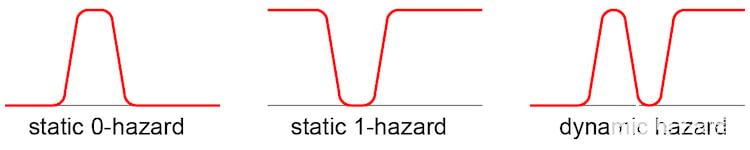
圖1. 三種類型的組合邏輯危害
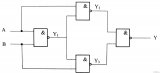
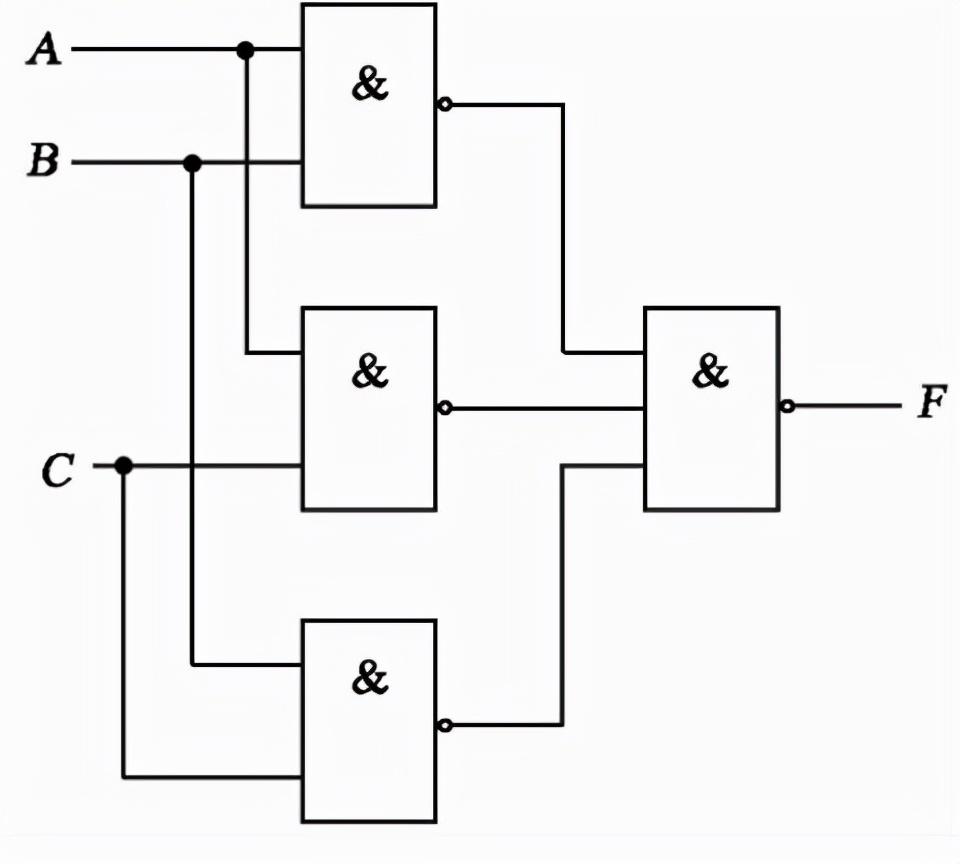
讓我們檢查圖2中的簡單電路,看看靜態(tài)0危險是如何產(chǎn)生的。

圖2. 具有靜態(tài)0-危險的組合邏輯電路
我們假設(shè)所有門都具有相同的傳播延遲時間常數(shù) d。在圖3的時序圖中,輸入a = b = 0。輸入 c 從邏輯 0 變?yōu)?1 后的一個柵極延遲,輸出 c‘
和 x 的狀態(tài)也發(fā)生變化。由于 x 和 y 現(xiàn)在(暫時)都設(shè)置為 1,這會導(dǎo)致最終輸出 f 從 0 變?yōu)?1 的后續(xù)變化。
但是,當(dāng)輸出 f 的狀態(tài)發(fā)生變化時,其輸入 y 也會發(fā)生變化,從 1 到 0。在 y 的這種變化通過最終門傳播后,輸出 f
返回到其最終狀態(tài)零。
以下是靜態(tài) 0 危害的示例:

圖3. 顯示靜態(tài) 0 危險時的序圖
如果我們查看圖2電路的Karnaugh圖,我們可以看到靜態(tài)0危險的機會。對于 0
輸出,有兩個相鄰但不相交的最小項,由藍色和棕褐色陰影突出顯示。對于和邏輯函數(shù)的乘積,共享最小項未覆蓋的任何兩個相鄰零都可能導(dǎo)致靜態(tài) 0 危險。
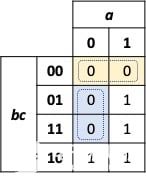
圖4. 顯示靜態(tài)-0危害的卡諾地圖
使用和的乘積從中推導(dǎo)出的邏輯函數(shù)為:

當(dāng) a 和 b 均為 0 時,輸入 c 可以在 0 和 1 狀態(tài)之間更改,而無需更改 f
的“最終”值。但是,由于某些電路實現(xiàn)的傳播延遲不同,因此可能存在靜態(tài)0危險。
修復(fù)組合邏輯電路中的靜電危害
我們可以消除圖2電路中的靜態(tài)-0危害,方法是在兩個相鄰項周圍添加一個額外的分組,如圖5中的紅色突出顯示框所示。

圖5. 用于消除靜態(tài) 0 危害的 Karnaugh 地圖分組
新的邏輯函數(shù)是:

從純數(shù)字邏輯的角度來看,序列中的第三個和項是不必要的。但是,當(dāng) a 和 b 均為 0 時,這個額外的總和  保持為 0。因此,它不受先前導(dǎo)致靜態(tài)-0危害的c變化的影響。
保持為 0。因此,它不受先前導(dǎo)致靜態(tài)-0危害的c變化的影響。
使用這種冗余邏輯,我們可以創(chuàng)建一個執(zhí)行相同邏輯功能的新電路,但沒有靜態(tài)0危險。這個新電路如圖6所示。
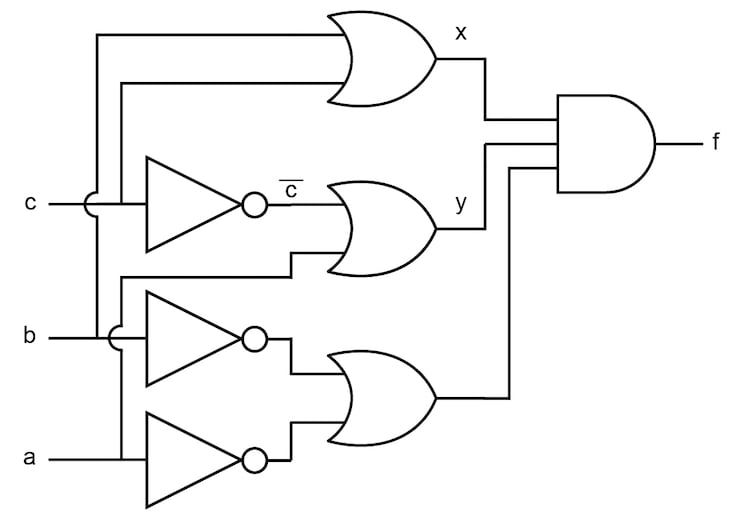
圖6. 消除靜態(tài)0危險的組合邏輯電路
發(fā)現(xiàn)并消除靜態(tài)-1危害
識別和修復(fù)靜態(tài) 1 危害與靜態(tài) 0 危害基本相同。使用 Karnaugh 映射查找未被同一最小項覆蓋的相鄰邏輯 1 輸出。對于發(fā)現(xiàn)的每個相鄰的 1
組合,添加一個額外的分組以消除潛在危險。
異步邏輯與同步邏輯
與危險相關(guān)的瞬態(tài)脈沖問題在同步電路中很少成為問題。它們旨在在每個時鐘周期內(nèi)留出足夠的時間來解決靜態(tài)和動態(tài)危險的毛刺。
另一方面,可以立即響應(yīng)信號變化的異步邏輯電路可能會受到很大影響。例如,等待響應(yīng)正 0 到 1 邏輯轉(zhuǎn)換的異步邏輯電路會在圖 3
的時序圖中錯誤地做出反應(yīng)。即使在主要同步設(shè)計中,系統(tǒng)復(fù)位和當(dāng)前信號通常也是異步的,因此容易受到危險的影響。
-
電路
+關(guān)注
關(guān)注
173文章
6005瀏覽量
173938 -
邏輯
+關(guān)注
關(guān)注
2文章
834瀏覽量
29622 -
組合邏輯電路
+關(guān)注
關(guān)注
6文章
71瀏覽量
14810
發(fā)布評論請先 登錄
相關(guān)推薦
基本組合邏輯電路
組合邏輯電路的分析與設(shè)計-邏輯代數(shù)

組合邏輯電路的設(shè)計
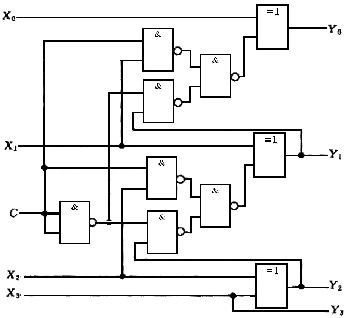
組合邏輯電路實驗原理
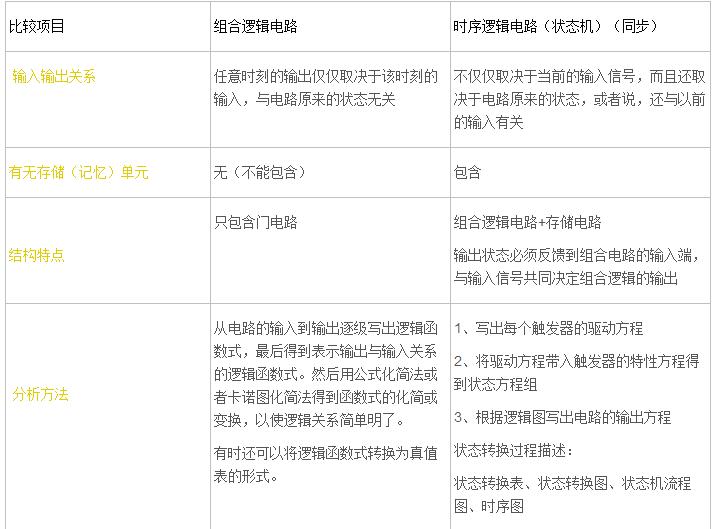
組合邏輯電路和時序邏輯電路比較_組合邏輯電路和時序邏輯電路有什么區(qū)別
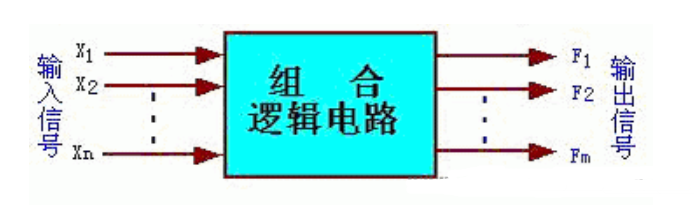
什么是組合邏輯電路 如何使用verilog描述組合邏輯電路


















評論