高速化、集成化電驅動系統中存在的NVH問題更加復雜,如:較高的輸入轉速導致系統固有頻率更加密集、局部模態增多;驅動電機的扭矩波動、徑向電磁力與齒輪傳遞誤差等多個振動激勵源作用下的復雜動態響應;電驅動系統整體變形的強耦合性等因素產生的NVH問題。相較于傳統的齒輪傳動系統,目前高速化、集成化的電驅動系統新出現NVH問題的重點、難點主要有以下三點:轉速逐步提高的高速驅動電機的影響;電機扭矩波動、徑向力與齒輪傳遞誤差等多個激勵源的影響;考慮系統整體耦合變形的動力學響應分析建模。目前電驅系統減速器高速軸齒傳動性能仿真技術正在處于發展階段,國內外主機廠大部分處于起步階段,減速器軸齒性能仿真模型精度不高、系統集成度不高、效率低、計算分析結果不夠準確。考慮驅動電機結構、齒輪-傳動軸-軸承的轉子系統以及差速器殼體、電驅動系統箱體等異形部件,搭建電驅動系統剛柔耦合動力學模型,并給出了考慮驅動電機徑向力、扭矩波動以及齒輪傳遞誤差等振動激勵源作用下的電驅動系統動力學響應的分析方法。
引言
在傳統內燃機汽車中,發動機噪聲較好地掩蓋了齒輪傳動系統的振動噪聲,但在純電動汽車中,由于發動機噪聲掩蔽效應的缺失,使得電磁噪聲及齒輪階次噪聲凸現。此外,高速化、集成化發展給電驅動系統的NVH帶來了新的挑戰。目前電驅動系統的高速驅動電機的轉速普遍高達12 000 r/min~18 000 r/min,預計在未來會進一步提高至20 000 r/min~25 000 r/min。高轉速導致高頻嘯叫,而且電驅動系統的動態響應頻率進一步提高至2k Hz~5k Hz,該頻率在人耳的敏感頻率范圍之內,嚴重影響了汽車的乘坐舒適性。電驅動系統剛柔耦合建模及動力學特性分析方法,包括電驅系統整體動力學建模、電驅動系統各部件剛柔耦合建模、電驅動系統動力學響應計算、電磁激勵下的電驅動系統動態響應分析、齒輪傳遞誤差激勵下系統動力學響應分析。
1 電驅系統整體動力學建模
針對多自由度系統的整體建模,首先需要將整個模型進行離散化。目前常用的離散化方法主要有集中參數法和有限元建模法,基于有限元原理對具有復雜構型的多自由系統進行動力學建模更加符合系統本質特性,本文借鑒有限元法原理進行電驅動系統整體動力學方程的建立。基于有限元原理的電驅系統動力學方程由相應的各零部件單元質量矩陣、剛度矩陣、阻尼矩陣構成。遵照以下原則:
(1)軸單元建模采用鐵木辛柯梁單元進行建模,考慮剪切變形,忽略摩擦因素;
(2)軸單元的質量矩陣采用一致質量矩陣,考慮相鄰節點的質量耦合;
(3)以節點的形式將齒輪嚙合剛度的等效彈簧添加到傳動軸上。電驅系統整體動力學方程如下:
Mq+Cq+Kq=f
(1)
式中,M為系統質量矩陣,C為阻尼矩,K為剛度矩陣,f為激振力矩陣。
求得各零部件單元的質量矩陣、剛度矩陣、阻尼矩陣,就可按照一定的方式組裝入系統全局質量矩陣、剛度矩陣、阻尼矩陣中,進而可以利用數值計算方法進行動力學方程求解。
2 系統各部件剛柔耦合建模
電驅動系統各部件剛柔耦合建模包括電機及箱體柔性有限元建模、異形軸類部件的有限元建模、齒輪嚙合單元動力學建模、軸承單元的動力學建模。
2.1 電機及箱體柔性有限元建模
將箱體的三維幾何模型導入到有限元軟件進行網格劃分。因電驅系統箱體是不規則殼體,所以這個過程首先需要做幾何清理,進而是網格劃分、網格質量檢查和網格處理的迭代過程,最終保證網格質量、數量要求。
設置各部分殼體的有限元模型材料,包括密度、楊氏模量、泊松比等材料屬性;在輸入軸、中間軸、輸出軸、電機轉子軸對應軸承座孔處建立凝聚節點的位置,使其與軸承外圈進行耦合。在電驅系統箱體懸置點處添加約束,及箱體模型接地等邊界條件;對有限元模型進行縮聚,最終得到箱體縮聚的剛度矩陣與質量矩陣。
2.2 異形軸類部件的有限元建模
與電驅動系統箱體不同之處,是差速器殼體由于是軸類零件,不需要進行接地處理,但額外需要與齒輪輪輻進行連接。
將差速器殼體的三維幾何模型導入到有限元軟件進行網格劃分。因差速器殼體也是不規則殼體,所以這個過程首先需要做幾何清理,進而是網格劃分、網格質量檢查和網格處理的迭代過程,最終保證網格質量、數量要求。
設置差速器殼體各部分有限元模型材料,包括密度、楊氏模量、泊松比等材料屬性。在差速器兩個軸承內圈連接處中心建立凝聚節點,同時在齒輪輪輻連接區域中心建立凝聚節點,以及在差速器內錐齒輪左右墊片處、上下定位銷處建立凝聚節點。并分別將軸承內圈的連接區域和齒輪輪輻連接區域基于運動耦合約束連接至凝聚節點處。對有限元模型進行縮聚,最終得到差殼縮聚的剛度矩陣與質量矩陣。
2.3 齒輪嚙合單元動力學建模
對于電驅動系統減速器中的斜齒輪嚙合單元,按其結構形式可劃分為輪齒嚙合部分及齒輪輪體部分。針對這兩部分需采用不同的建模方式進行建模。
(1)針對輪輻,輪輻不是具有規則回轉結構的回轉體,其包含減重孔。同差速器殼體一樣進行有限元建模,其中輪輻只需連接軸外圈及齒輪嚙合位置的柔性節點圈。
(2)針對斜齒輪齒的建模,采用參數化建模。其中主要分成兩部分,為漸開線嚙合部分、齒根圓弧部分。各部分的網格數量及大小可通過軟件識別齒輪的宏觀參數任意控制,同時生成這兩部分的有限元網格模型。
2.4 軸承單元的動力學建模
由于軸承相比電驅動系統其他各部件質量小得多,故對軸承質量忽略不計。另軸承內圈與軸相配合,軸承外圈與殼體凝聚節點相耦合。其耦合方式有三種,分別為剛性模型、非耦合彈性支撐模型以及耦合彈性支撐模型,其中耦合彈性支撐模型最為普遍。同時考慮到電驅系統箱體柔性對軸承位移作用的影響,最終得到軸承和箱體單元的運動動力學方程。
3 電驅系統動力學響應計算
3.1 齒輪副動態嚙合剛度計算
動態嚙合剛度指嚙合齒輪受到單位微米大小的正弦傳遞誤差激勵而計算出的動態力,動態嚙合剛度是隨齒輪嚙合頻率ω變化而動態變化的輪齒嚙合剛度。
ω=n/60×Z
(2)
D(ω)=C(ω)-1
(3)
C(ω)=C1 (ω)+C2(ω)
(4)
式中,n為轉速,Z為齒數,ω為齒輪嚙合頻率,D(ω)為當頻率是ω時的齒輪嚙合線上的動態嚙合剛度,C(ω)為兩齒輪總柔度,C1(ω)和C2(ω)為主從齒輪在嚙合線上的柔度。
3.2 齒輪副動態嚙合力計算
齒輪副動態嚙合力是指嚙合齒輪副受到靜態傳遞誤差諧波激勵而計算出的輪齒動態力。
Fi(ω)=D(ω)×δi
(5)
式中,Fi(ω)為齒輪傳遞誤差第i階諧波的動態嚙合力、δi為齒輪嚙合傳遞誤差的第i階諧波。
3.3 系統固有頻率及模態振型計算
(K-ω2rM)φr=0
(6)
式中,ωr為第r階固有頻率,φr為第r階固有振型,M為質量矩陣,K為剛度矩陣。上式要求特征值ωr所對應的特征向量φr是正交的,系統的質量矩陣M及剛度矩陣K同時正交的,即可得到系統的固有頻率及模態振型。
4 電磁激勵下的電驅動系統動態響應分析
4.1 電機扭矩波動激勵下的系統動態響應分析
由電驅動系統振動噪聲的傳遞路徑可以得出,振動噪聲傳至殼體之后,一方面通過殼體振動直接向空氣中輻射噪聲,另一方面通過電驅動系統與車輛的連接點向車輛其他部件傳遞振動,引起車輛其他部件的共振或者借助其他部件向外輻射噪聲。同時電驅動系統與車輛的連接點一般為系統懸置點或者固定連接處,因此分析懸置點處的振動加速度可對NVH性能進行評價。分別對電機的扭矩波動的24階、48階諧波所引起的對電驅系統的三個懸置點位置處的振動加速度響應做分析。
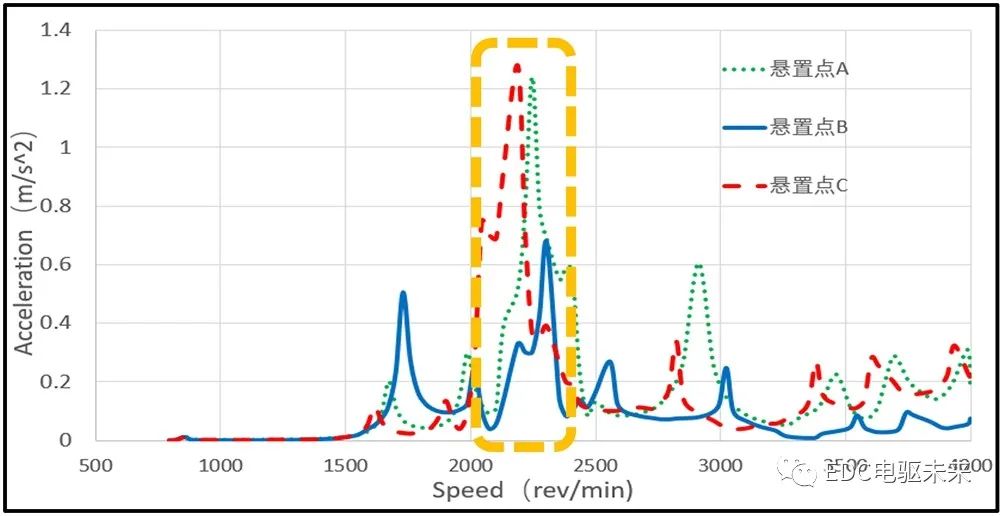
圖6 轉矩脈動24階系統動力學響應
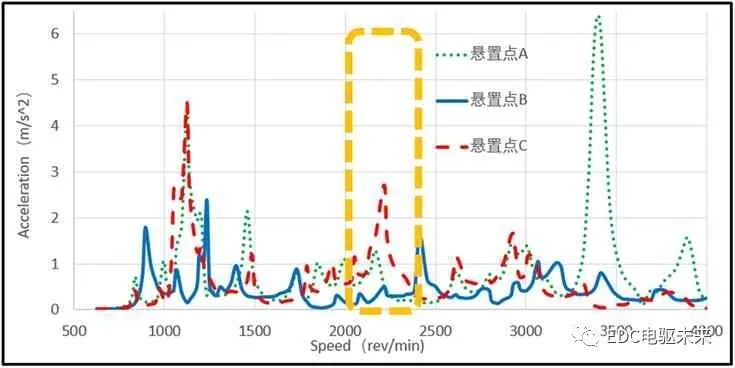
圖7 轉矩脈動48階系統動力學響應
(1)由圖6、圖7可知,電機轉矩脈動24階諧波和48階諧波的NVH激勵源作用下,懸置點A處的振動加速度均值要比另外兩個懸置點B、C均值較大一些,這是,因為懸置點A處離NVH激勵源較近,因此受激勵源的影響較大;
(2)由圖6、圖7對比可知,轉矩脈動48階諧波激勵下的振動加速度均值要比24階高出一個量級,轉矩脈動24階諧波激勵下最大振動加速度出現在2 200 r/min,其最大振動加速度幅值為1.285 m/s2;而在轉矩脈動48階諧波激勵下最大振動加速度出現在3 750 r/min,其最大振動加速度幅值為6.234 m/s2;這是由于扭矩波動的48階諧波力比24階的諧波力更大;
(3)在24階次下,在輸入軸轉速2 300 r/min左右時,懸置點A、B、C在898 Hz頻率時出現了共振峰,其振動加速度幅值分別為1.225 m/s2、0.67 m/s2、1.285 m/s2,此共振峰峰值較大。同樣在48階次下,在輸入軸轉速2 300 r/min 左右時,懸置點A、B、C在898 Hz頻率時出現了共振峰,其振動加速度幅值分別為1.5 m/s2、0.4 m/s2、2.85 m/s2,此處共振峰值較大,需要重點關注該頻率的共振。
4.2 徑向電磁力激勵下的系統動態響應分析
同電機扭矩波動相同,分別對電機的徑向電磁力激勵的24階、48階諧波所引起的對電驅系統的各個懸置點位置處的振動加速度響應做分析。
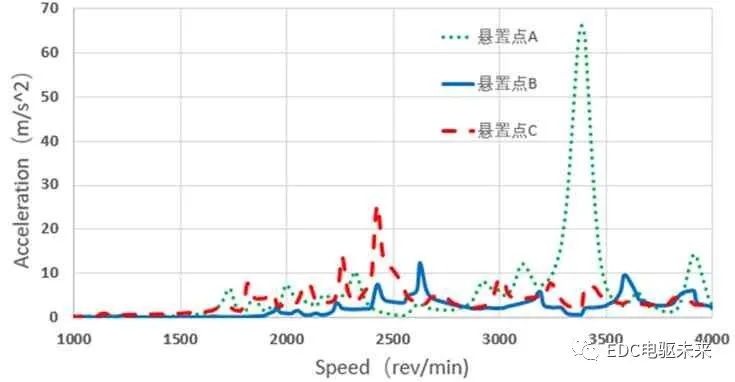
圖8 徑向電磁力24階系統動力學響應
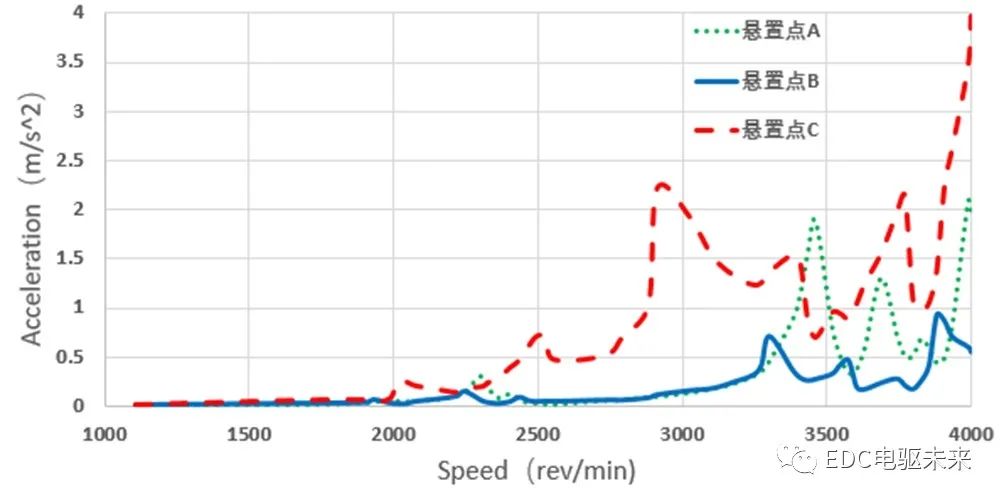
圖9 徑向電磁力48階系統動力學響應
(1)隨著諧波階次的增加,振動加速度幅值在0~4 000 r/min 范圍內也是依次增加的,而徑向電磁力24階、48階的諧波力幅值則是降低的,這是由于諧波階次增加,其工作頻率也在相應增加,因此其幅值也相應地更高,而在相同的工作頻率下對比,則其振動加速度幅值與諧波力幅值的表現一致。
(2)懸置點A、C在轉速為3 690 r/min出現了共振峰,其24階振動加速度峰值分別為1.35 m/s2、2.12 m/s2,其共振的固有頻率可能為2 950 Hz;懸置點B、C在轉速為2 450 r/min 出現了共振峰,其48階振動加速度峰值分別為7.05 m/s2、26.0 m/s2,其共振的固有頻率可能為1 950 Hz;懸置點A在轉速為3 460 r/min 時出現了一個較大的共振峰,其48階振動加速度幅值為68 m/s2,其共振的固有頻率可能為2 800 Hz,需重點關注這幾個頻率的共振。
5 齒輪傳遞誤差激勵下系統動力學響應分析
分別對減速器齒輪嚙合的一、二級兩對齒輪副的傳遞誤差進行傅里葉變換,分別獲得起傳遞誤差各階諧波,由于傳遞誤差的二階及以上諧波幅值較小,可忽略不計。故只考慮將一二級齒輪的一階諧波作為NVH的激勵源。分析一、二級齒輪副的激勵源所引起的對電驅系統的各個懸置點位置處的振動加速度響應。
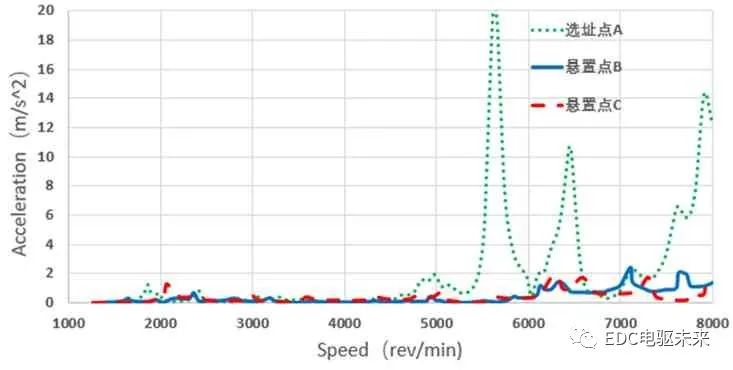
圖10 一級齒輪TE的動力學響應
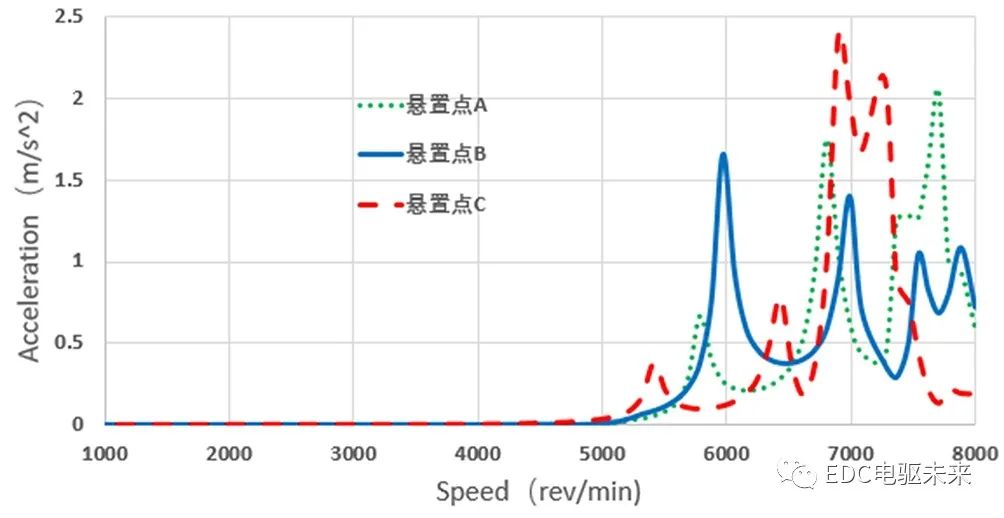
圖11 二級齒輪TE的動力學響應
(1)在輸入軸低轉速的情況下,系統振動及速度幅值較低,隨轉速增加,振動加速度幅值總體呈上升趨勢;
(2)傳遞誤差越小,一階諧波幅值越小,振動加速度幅值越小,越有利于NVH;
(3)將一、二級齒輪副嚙合引起的振動加速度幅值同電機扭矩波動、徑向電磁力激勵下的振動加速度幅值進行比較,可得出二者對系統NVH的貢獻量,振動加速度幅值越大,貢獻量越大;
(4)在二級齒輪副嚙合階次下,在轉速為6 950 r/min附近時,三個懸置點出現了第一次共振峰,三個懸置點處的加速度峰值分別為1.76 m/s2、1.41 m/s2、2.39 m/s2,在此轉速附近,具有2 750 Hz與3 290 Hz的固有頻率;這種情況是激發起系統的某一固有頻率引起的,需重點關注該固有頻率的共振情況。
6 結論
針對電驅動系統NVH分析及優化中存在的高轉速、多源激勵以及整體強耦合性等難題,基于有限元及動力學建模方法,搭建了電驅動整體剛柔耦合動力學模型。本文分別對驅動電機及箱體的有限元建模以及齒輪傳動系統動力學建模兩大方面進行了詳細建模。針對驅動電機建模部分,采用有限元模型縮聚的方式進行了電驅動箱體與電機定子的建模工作,同時還有對電磁力的施加處理方法。針對齒輪傳動系統,建立了彈性軸段、斜齒輪嚙合單元、差速器殼體單元以及軸承單元的動力學模型。基于以上建模流程,形成了電驅動系統整體剛柔耦合建模方法。接下來給出了電驅動系統動力學響應的計算方法。最后,針對驅動電機徑向力、轉矩脈動以及齒輪副傳遞誤差等 NVH 激勵源作用下的系統動態響應進行了對比分析。
審核編輯:郭婷
-
發動機
+關注
關注
33文章
2477瀏覽量
69339 -
減速器
+關注
關注
7文章
394瀏覽量
23269 -
驅動電機
+關注
關注
9文章
410瀏覽量
30733
原文標題:電驅動系統耦合建模及動力學特性分析
文章出處:【微信號:EDC電驅未來,微信公眾號:EDC電驅未來】歡迎添加關注!文章轉載請注明出處。
發布評論請先 登錄
相關推薦
電力拖動系統的動力學課件
[下載]想了解多體動力學軟件嗎?有教程分享及免費試用下載
基于多體系統動力學的空氣懸架大客車平順性試驗仿真研究
帶齒輪傳動的機車-軌道空間耦合動力學模型
分布式驅動電動汽車的動力學控制有哪幾種類型?常見問題是什么?
空間柔性機器人動力學分析的快速積分算法
機械系統動力學分析及ADAMS應用電子教程免費下載
基于車輛動力學模型的橫向控制




 電驅動系統耦合建模及動力學特性分析
電驅動系統耦合建模及動力學特性分析










評論