一、什么是“關聯速度”問題

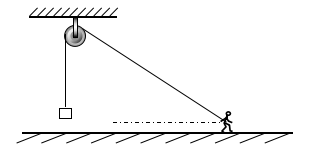
所謂“關聯速度”就是兩個通過某種方式聯系起來的速度。比如一根繩兩端的速度通過繩發生聯系。 如下圖所示，人通過跨過光滑定滑輪的輕繩拖動重物，人向右勻速運動，當繩與水平方向的夾角為θ角時，物塊上升的速度是多少。

二、已經掌握的知識

1、兩個物體用不可伸長輕繩連接在一起，在水平面上運動，這兩個物體任何時刻速度相等。因為輕繩是理想化模型，不可發生明顯形變，所有任何一段時間兩物體的位移必相同，由此判定速度必相同，并且兩個物體的速度與繩上任意一點的速度都相同。

2、不可伸長的輕繩一端固定在天花板上，另一端連接小球，讓小球在豎直平面內擺動，繩上各點的運動情況（線速度）就不同了，離懸點越遠的點線速度越大。

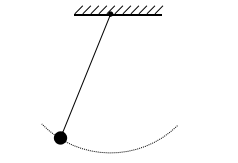
以上兩個實例告訴我們，同一繩子上各點的速度不一定相同。只有當繩子上各點都沿繩的方向運動時，各點的速度大小才相同，而當繩子繞點轉動時繩上各點的線速度大小不同。

三、可以這樣分解合速度

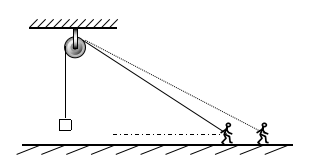
基于以上的前提知識，我們假設人站在原地不動，雙手收繩子而使物體上升，則物塊上升的速度與人收繩子的速度相等；假如人以滑輪為懸點，保持懸點到人手之間的繩長不變，在豎直平面內轉動繩子，則物塊不會上升。也就是說，繩子的轉動不會改變物塊的速度，只有沿繩方向收繩子時物塊才會上升。

所以，當人運動拉繩時，繩子沿繩的方向運動，同時繞懸點旋轉。此時可以把人看做繩上的一個點，人的運動可以看作合運動，能分解為沿繩的方向的運動和繞懸點的轉動。物塊上升的速度與人的速度沿繩方向的分量大小相等，從而得出物塊的速度v 物 =v人cosθ。

四、也可以用“微元法”求解

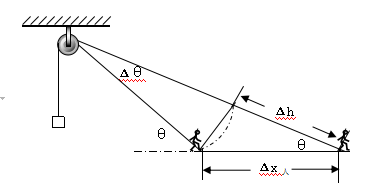
用數學方法更容易表述物理思想。取很短的時間Δt研究，在該時間內人運動的位移

Δx 人 =V人Δt

由于Δt趨近于零，故繩子轉過的角度Δθ也趨近于零，物體上升的高度Δh

Δh=Δx人cosθ

而物體的速度可以這樣表示

v 物 =Δh /Δt

綜合以上關系式得到 v 物 =v人cosθ

這樣理解關聯速度是不是很容易？

審核編輯：劉清