導讀

本文介紹了算法和數據結構的基礎概念和復雜度函數，并提供了一些評價算法和數據結構優劣的方法論，之后又重點介紹了幾種工作中常見且重要的數據結構和算法。作為系列文章的開篇，希望讀者能夠在理解復雜度函數的基礎上，重點關注每一種數據結構的優劣勢分析。

01 前言

ES現在已經被廣泛的使用在日常的搜索中，Lucene作為它的內核值得深入研究，比如FST，下面就用兩篇分享來介紹一些本文的主題：

第一篇主要介紹數據結構和算法基礎和分析方法，以及一些常用的典型的數據結構；

第二篇主要介紹圖論，以及自動機，KMP，FST等算法；

下面開始第一篇：

02 提出問題

“算法是計算機科學領域最重要的基石之一“

“編程語言雖然該學，但是學習計算機算法和理論更重要，因為計算機算法和理論更重要，因為計算機語言和開發平臺日新月異，但萬變不離其宗的是那些算法和理論，例如數據結構、算法、編譯原理、計算機體系結構、關系型數據庫原理等等。“

——《算法的力量》

2.1.1 案例一

設有一組N個數而要確定其中第k個最大者，稱之為選擇問題。常規的解法如下：

該問題的一種解法就是將這N個數讀進一個數組中，在通過某種簡單的算法，比如冒泡排序法，以遞減順序將數組排序，然后返回位置k上的元素。

稍微好一點的算法可以先把前k個元素讀入數組并對其排序。接著，將剩下的元素再逐個讀入。當新元素被讀到時，如果它小于數組中的第k個元素則忽略之，否則就將其放到數組中正確的位置上，同時將數組中的一個元素擠出數組。當算法終止時，位于第k個位置上的元素作為答案返回。

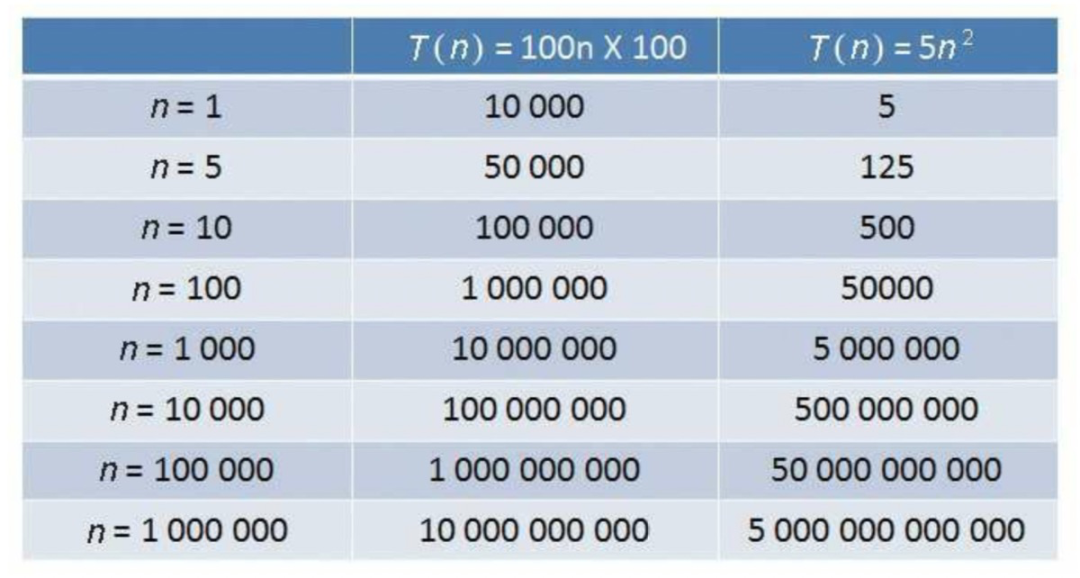
這兩種算法編碼都很簡單，但是自然要問：哪個算法更好？哪個算法更重要？還是兩個算法都足夠好？使用N=30000000和k=15000000進行模擬將發現，兩個算法在合理的時間量內均不能結束；每一種算法都需要計算機處理若干時間才能完成。

其實還有很多可以解決這個問題，比如二叉堆，歸并算法等等。

2.2.2案例二

輸入是由一些字母構成的一個二維數組以及一組單詞組成。目標是要找出字謎中的單詞，這些單詞可能是水平、垂直、或沿對角線上任何方向放置。下圖所示的字謎由單詞this、two、fat和that組成。

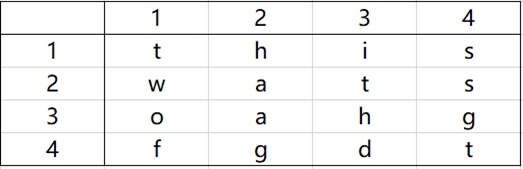
圖1 字謎單詞字符排列示意圖

現在至少也有兩種直觀的算法來求解這個問題：

對單詞表中的每個單詞，檢查每一個有序三元組（行，列，方向）驗證是否有單詞存在。這需要大量嵌套的for循環，但它基本上是直觀的算法。

對于每一個尚未越出迷板邊緣的有序四元組（行，列，方向，字符數）可以測試是否所指的單詞在單詞表中。這也導致使用大量嵌套的for循環。

上述兩種方法相對來說都不難編碼，但如果增加行和列的數量，則上面提出的兩種解法均需要相當長的時間。

以上兩個案例中，可以看到要寫一個工作程序并不夠。如果這個程序在巨大的數據集上運行，那么運行時間就變成了重要問題。

那么，使用自動機理論可以快速的解決這個問題，下一篇中給大家詳細的分析。

03 數據結構與算法基礎

3.1 數據結構基礎

3.1.1 什么是數據結構

在計算機領域中，數據是信息的載體，是能夠輸入到計算機中并且能被計算機識別、存儲和處理的符號的總稱。數據結構是指數據元素和數據元素之間的相互關系或數據的組織形式。數據元素是數據的的基本單位，數據元素有若干基本項組成。

3.1.2 數據之間的關系

數據之間的關系分為兩類：

邏輯關系

表示數據之間的抽象關系，按每個元素可能具有的前趨數和直接后繼數將邏輯結構分為線性結構和非線性結構。

邏輯關系或邏輯結構有如下特點：

只是描述數據結構中數據元素之間的聯系規律；

是從具體問題中抽象出來的數學模型，是獨立于計算機存儲器的（與硬件無關）

邏輯結構的分類如下：

線性結構

樹形結構

圖狀結構

其他結構

·物理關系

邏輯關系在計算中的具體實現方法，分為順序存儲方法、鏈式存儲方法、索引存儲方法、散列存儲方法。

物理關系或物理結構有如下特點：

是數據的邏輯結構在計算機存儲其中的映像；

存儲結構是通過計算機程序來實現，因而是依賴于具體的計算機語言的；

物理結構分類如下：

順序結構

鏈式結構

索引結構

3.2 算法基礎

3.2.1 基礎概念

算法是為求解一個問題需要遵循的、被清楚指定的簡單指令的集合。對于一個問題，一旦某種算法給定并且被確定是正確的，那么重要的一步就是確定該算法將需要多少諸如時間或空間等資源量的問題。如果一個問題的求解算法竟然需要長達一年時間，那么這種算法就很難能有什么用處。同樣，一個需要若干個GB的內存的算法在當前的大多數機器上也是無法使用的。

3.2.2 數學基礎

一般來說，估算算法資源消耗所需的分析是一個理論問題，因此需要一套數學分析法，先從數學定義開始。

定理1：如果存在正常數c和n0，使得當N>= n0時，T(N) <= cf(N)，則記為T(N) = O(f(N))。

定理2：如果存在正常數c和n0，使得當N>=n0時，T(N) <= cg(N)，則記為T(N) = Ω(g(N))。

定理3：T(N) = θ(h(N))當且僅當T(N) = O(h(N)) 和 T(N) = Ω(h(N))。

定理4：如果對每一個正常數c都存在常數n0使得當N>n0時，T(N) < cp(N)，則T(N) = o(p(N))。

這些定義的目的是要在函數間建立一種相對的級別。給定兩個函數，通常存在一些點，在這些點上一個函數的值小于另一個函數的值，因此，一般宣稱f(N)相對增長率。當將相對增長率應用到算法分析時，會明白它是重要的度量。

如果用傳統的不等式來計算增長率，那么第一個定義T(N) = O(f(N))是說T(N)的增長率小于或者等于f(N)的增長率。第二個定義T(N) = Ω(g(N))是說T(N)增長率大于或者等于g(N)的增長率。第三個定義T(N) = θ(h(N))是說T(N)的增長率等于h(N)的增長率。最后一個定義T(N) = o(p(N))說的則是T(N)的增長率小于p(N)的增長率。他不同于大O，因為大O包含增長率相同的可能性。

要證明某個函數T(N) =O(f(N))，通常不是形式的使用這些定義，而是使用一些已知的結果（比如說T(N) = O(log(N))）。一般來說，這就意味著證明是非常簡單的計算而不應涉及微積分，除非遇到特殊情況。如下是常見的已知函數結果

c（常數函數）

logN（對數函數）

logN^2（對數平方函數）

N（線性函數）

NlogN

N^2（二次函數）

N^3（三次函數）

2^N（指數函數）

在使用已知函數結果時，有幾點需要注意：

首先，將常數或低階項放進大O是非常壞的習慣。不要寫成T(N) = O(2*N^2)或T(N) = O(N^2 + N)。這兩種情形下，正確的形式是T(N) = O(N^2)。也就是說低階項一般可以被忽略，而常數也可以棄掉。

其次，總能夠通過計算極限limN→∞f(N)/g(N)（極限公式）來確定兩個函數f(N)和g(N)的相對增長率。該極限可以有四種可能的值：

極限是0：這意味著f(N) = o(g(N))。

極限是c != 0：這意味著f(N) = θ(g(N))。

極限是∞：這意味著g(N) = o(f(N))。

極限擺動：二者無關。

3.2.3 復雜度函數

正常情況下的復雜度函數包含如下兩種：

時間復雜度

空間復雜度

時間和空間的度量并沒有一個固定的標準，但是在正常情況下，時間復雜度的單位基本上是以一次內存訪問或者一次IO來決定。空間復雜度是指在算法執行過程中需要占用的存儲空間。對于一個算法來說，時間復雜度和空間復雜度往往是相互影響，當追求一個好的時間復雜度時，可能會使空間復雜度變差，即可能占用更多的存儲空間；反之，當追求一個較好的空間復雜度時，可能會使時間復雜度變差，即可能占用較長的運算時間。

3.3 知識儲備

3.3.1 質數分辨定理（HashTree的理論基礎）

簡單的說就是，n個不同的質數可以分辨的連續數的個數和他們的乘機相同。分辨是指這些連續的整數不可能有相同的余數序列。

3.3.2Hash算法

1）Hash

Hash一般翻譯成散列，也可以直接音譯成哈希，就是把任意長度的輸入，通過散列算法變換成固定長度的輸出，該輸入就是散列值。不同的輸入可能散列成相同的值，確定的散列值不可能確定一個輸入。

2）常見的Hash算法

MD4：消息摘要算法；

MD5：消息摘要算法，MD4的升級版本；

SHA-1：SHA-1的設計和MD4相同原理，并模仿該算法；

自定義HASH算法：程序設計者可以自定義HASH算法，比如java中重寫的hashCode()方法。

3）Hash碰撞

解決Hash碰撞常見的方法有一下幾種：

分離鏈接法（鏈表法）：做法是將散列到同一個值的所有元素保留在一個表中，例如JDK中的HashMap；

探測散列表：當發生Hash碰撞時，嘗試尋找另外一個單元格，直到知道到空的單元為止。包括：線性探測法，平方探測法，雙散列。

3.3.2樹結構的基本概念

樹的遞歸定義：一棵樹是一些節點的集合。這個集合可以是空集；若不是空集，則樹由根節點root以及0個或多個非空的子樹組成，這些子樹中每一棵的根都被來自根root的一條有向的邊所連接；

樹葉節點：沒有兒子節點稱為樹葉；

深度：對于任意節點ni，ni的深度為從根到ni的唯一路徑的長；

高度：對于任意節點ni，ni的高度為從ni到一片樹葉的最長路徑的長；

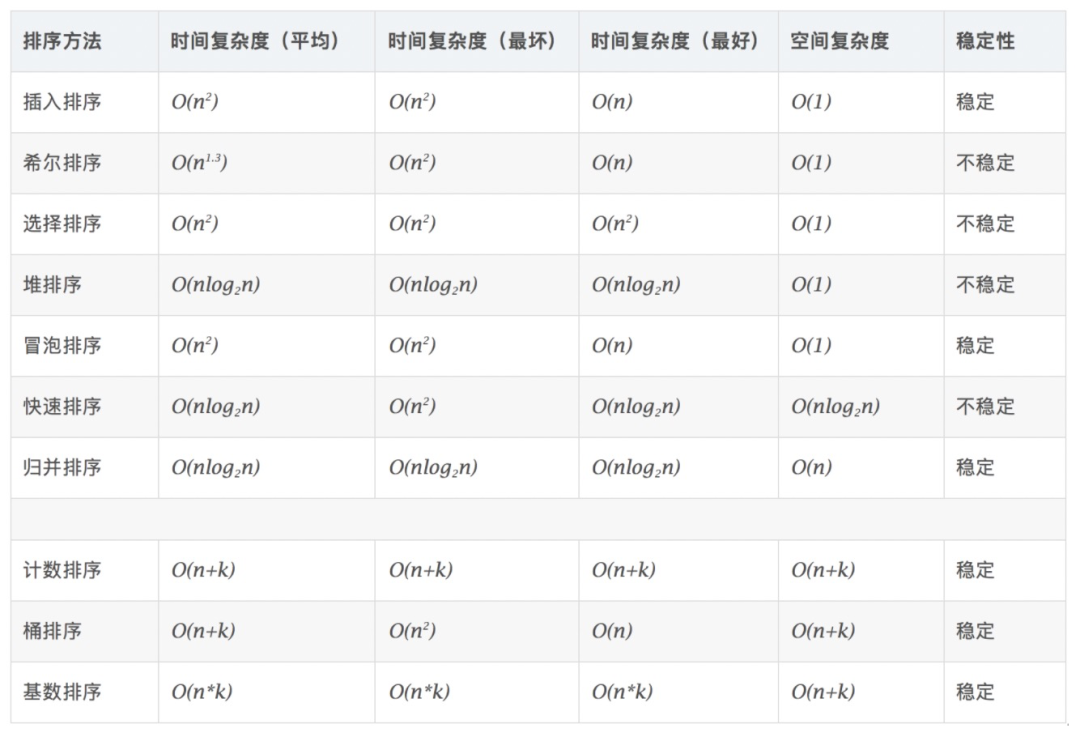
樹的遍歷：樹的遍歷分為兩種，先序遍歷和后續遍歷。

3.3.4二叉搜索樹

二叉搜索樹是一棵二叉樹，其中每個節點都不能有多于兩個子節點。

對于二叉查找樹的每一個節點X，它的左子樹中所有項的值都小于X節點中的項，而它的右子樹中所有項的值大于X中的項。

04 常見數據結構與算法分析

4.1 線性數據結構

4.1.1 HashMap

·總述

HashMap是開發中最常用的數據結構之一，數據常駐于內存中，對于小的數據量來說，HashMap的增刪改查的效率都非常高，復雜度接近于O(1)。

·數據結構和算法

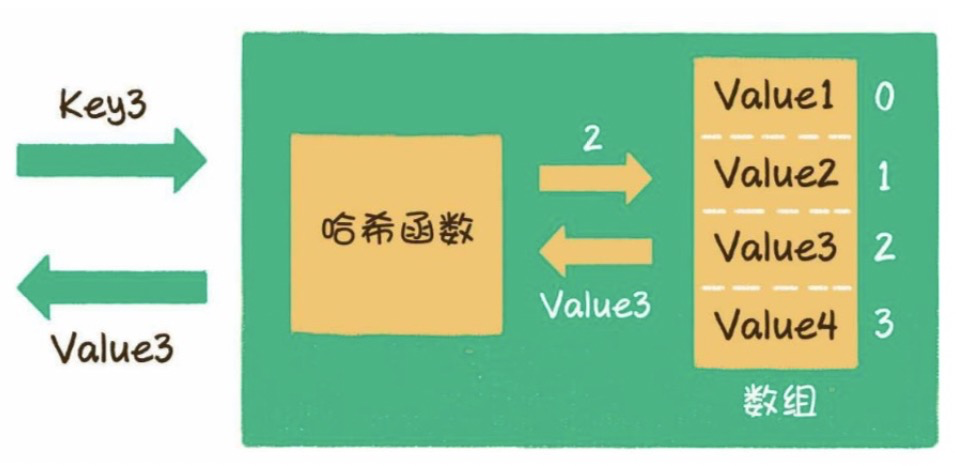
o HashMap由一個hash函數和一個數組組成；

o 數據插入，當進入到map的時候，根據hash(key)找到對應點位置，如果位置為空，直接保存，如果位置不為空，則使用鏈表的方式處理；為了解決遍歷鏈表所增加的時間，JDK中的鏈表在大小增大到8時，將會演變成紅黑樹以降低時間復雜度。為什么開始使用鏈表，后面使用紅黑樹：

§ 數據量較小的時候，鏈表的查詢效率相對來說也比較高，使用紅黑樹占用空間比鏈表要大；

§ 為什么選擇8，請參考泊松分布；

o 查找和刪除的過程，同插入的過程類似；

oHashMap可以支持自動擴容，擴容機制需要看具體的實現；

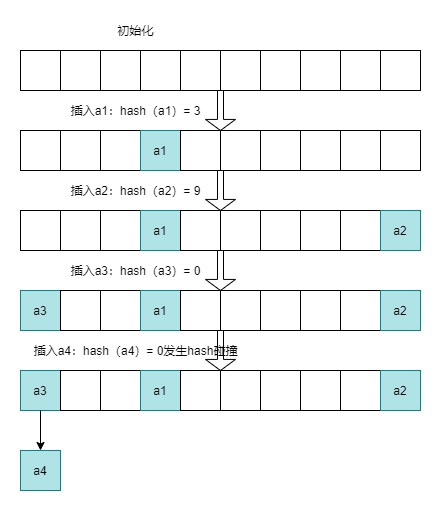
圖2HashMap的構建過程示意圖

優缺點

優點：動態可變長存儲數據，快速的查詢速度，查詢復雜度接近O(1);

缺點：只支持小數據量的內存查詢；

使用場景

在內存中小數據量的數據保存和快速查找。

4.1.2 BloomFilter（布隆過濾器）

·總述

布隆過濾器算法為大數據量的查找提供了快速的方法，時間復雜度為O(k)，布隆過濾器的語義為：

布隆過濾器的輸出為否定的結果一定為真；

布隆過濾器的輸出為肯定的結果不一定為真；

·數據結構和算法

布隆過濾器的具體結構和算法為：

布隆過濾器包含k個hash函數，每個函數可以把key散列成一個整數（下標）；

布隆過濾器包含了一個長度為n的bit數組（向量數組），每個bit的初始值為0；

當某個key加入的時候，用k個hash函數計算出k個散列值，并把數組中對應的比特置為1；

判斷某個key是否在集合時，用k個hash函數算出k個值，并查詢數組中對應的比特位，如果所有的bit位都為1，認為在集合中；

布隆過濾器的大小需要提前評估，并且不能擴容；

布隆過濾器的插入過程如下：

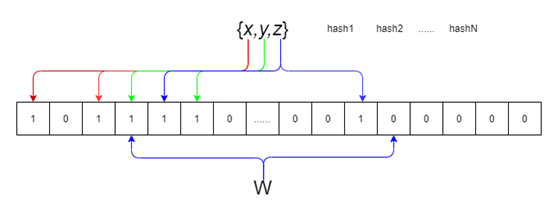
圖3布隆過濾器的構建過程示意圖

判斷某個key是否在集合時，用k個hash函數算出k個值，并查詢數組中對應的比特位，如果所有的bit位都為1，認為在集合中

布隆過濾器無法刪除數據；

布隆過濾器查詢的時間復雜度為O(k)；

布隆過濾器空間的占用在初始化的時候已經固定不能擴容。

·優缺點

優點：布隆過濾器在時間和空間上都有巨大的優勢。布隆過濾器存儲空間和插入/查找時間都是常數。布隆過濾器不需要存儲數據本身，節省空間。

缺點：布隆過濾器的缺點是有誤差。元素越多誤差越高。可以通過提高hash函數的個數和擴大bit數組的長度來降低誤差率；

·場景

使用場景：緩存擊穿，判斷有無。

4.1.3 SkipList（跳表）

·總述

跳表是一種特殊的鏈表，相比一般的鏈表有更高的查找效率，可比擬二差查找樹，平均期望的插入，查找，刪除的時間復雜度都是O(logN);

·數據結構和算法

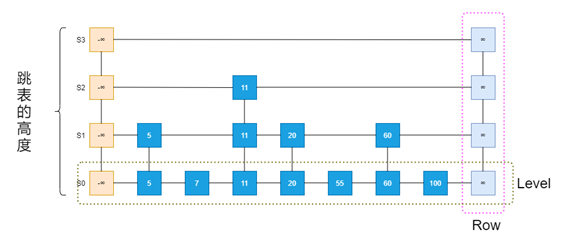
跳表可視為水平排列（Level）、垂直排列（Row）的位置（Position）的二維集合。每個Level是一個列表Si，每個Row包含存儲連續列表中相同Entry的位置，跳表的各個位置可以通過以下方式進行遍歷。

After(P)：返回和P在同一Level的后面的一個位置，若不存在則返回NULL；

Before(P)：返回和P在同一Level的前面的一個位置，若不存在則返回NULL；

Below(P)：返回和P在同一Row的下面的一個位置，若不存在則返回NULL；

Above(P)：返回和P在同一Row的上面的一個位置，若不存在則返回NULL。

圖4跳躍列表結構示意圖

有順序關系的多個Entry(K,V)集合M可以由跳表實現，跳表S由一系列列表{S0，S1，S2，......，Sh}組成，其中h代表的跳表的高度。每個列表Si按照Key順序存儲M項的子集，此外S中的列表滿足如下要求：

列表S0中包含了集合M的每個一個Entry；

對于i = 1 ，...... ，h-1列表Si包含列表Si-1中Entry的隨機子集；

Si中的Entry是從Si-1中的Entry集合中隨機選擇的，對于Si-1中的每一個Entry，以1/2的概率來決定是否需要拷貝到Si中，我們期望S1有大約n/2個Entry，S2中有大約n/4個Entry，Si中有n/2^i。跳表的高度h大約是logn。從一個列表到下一個列表的Entry數減半并不是跳表的強制要求；

插入的過程描述，以上圖為例，插入Entry58：

找到底層列表S0中55的位置，在其后插入Entry58；

假設隨機函數取值為1，緊著回到20的位置，在其后插入58，并和底層列表S0的Entry58鏈接起來形成Entry58的Row；

假設隨機函數取值為0，則插入過程終止；

下圖為隨機數為1的結果圖：

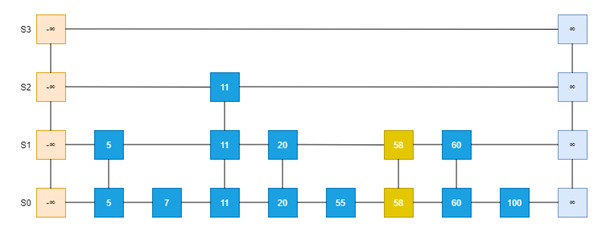
圖5插入一個元素的過程示意圖

刪除過程：同查找過程。

時間復雜度

o 查找包括兩個循環，外層循環是從上層Level到底層Level，內層循環是在同一個Level，從左到右;

o 跳表的高度大概率為O(logn)，所以外層循環的次數大概率為O(logn);

o 在上層查找比對過的key，不會再下層再次查找比對，任意一個key被查找比對的概率為1/2，因此內存循環比對的期望次數是2也就是O(1);

o 因此最終的時間復雜度函數O(n) = O(1)*O(logn)也就是O(logn)；

空間復雜度

o Level i期望的元素個數為 n/2^i；

o 跳表中所有的Entry（包含同一個Entry的Row中的元素） Σn/2^i = nΣ1/2^i，其中有級數公式得到Σ1/2^i < 2；

o 期望的列表空間為O(n)；

·優缺點

優點：快速查找，算法實現簡單；

缺點：跳表在鏈表的基礎上增加了多級索引以提升查詢效率，使用空間來換取時間，必然會增加存儲的負擔。

·使用場景

許多開源的軟件都在使用跳表：

Redis中的有序集合zset；

LevelDB Hbase中的memtable；

Lucene中的Posting List。

4.2 簡單非線性數據結構

4.2.1 AVL

·總述

AVL樹是帶有平衡條件的二叉查找樹，這個平衡條件必須要容易保持，而且它保證樹的深度必須是O(logN)。在AVL樹中任何節點的兩個子樹的高度最大差別為1。

·數據結構和算法

AVL樹本質上還是一棵二叉查找樹，有以下特點：

AVL首先是一棵二叉搜索樹；

帶有平衡條件：每個節點的左右子樹的高度之差的絕對值最多為1；

當插入節點或者刪除節點時，樹的結構發生變化導致破壞特點二時，就要進行旋轉保證樹的平衡。

針對旋轉做詳細分析如下：

把必須重新平衡的節點叫做a，由于任意節點最多有兩個兒子，因此出現高度不平衡就需要a點的兩棵子樹的高度差2。可以看出，這種不平衡可能出現一下四種情況：

對a的左兒子的左子樹進行一次插入；

對a的左兒子的右子樹進行一次插入；

對a的右兒子的左子樹進行一次插入；

對a的右兒子的柚子樹進行一次插入。

情形1和4是關于a的對稱，而2和3是關于a點的對稱。因此理論上解決兩種情況。

第一種情況是插入發生在外側的情況，該情況通過對樹的一次單旋轉而完成調整。第二種情況是插入發生在內側的情況，這種情況通過稍微復雜些的雙旋轉來處理。

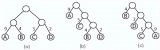
單旋轉的簡單示意圖如下：

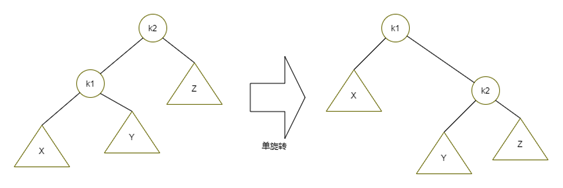
圖6單旋轉示意圖

雙旋轉的簡單示意圖如下：

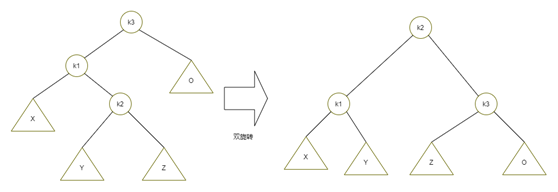
圖7雙旋轉示意圖

·優缺點

優點：使用二叉查找算法時間復雜度為O(logN)，結構清晰簡單；

缺點：插入和刪除都需要進行再平衡，浪費CPU資源；

·使用場景

少量數據的查找和保存；

4.2.2 Red BlackTree

·總述

紅黑樹是一種自平衡的二叉查找樹，是2-3-4樹的一種等同，它可以在O(logN)內做查找，插入和刪除。

·數據結構和算法

在AVL的基礎之上，紅黑樹又增加了如下特點：

每個節點或者是紅色，或者是黑色；

根節點是黑色；

如果一個節點時紅色的，那么它的子節點必須是黑色的；

從一個節點到一個null引用的每一條路徑必須包含相同數目的黑色節點。

紅黑樹的示意圖如下（圖片來源于網絡）：

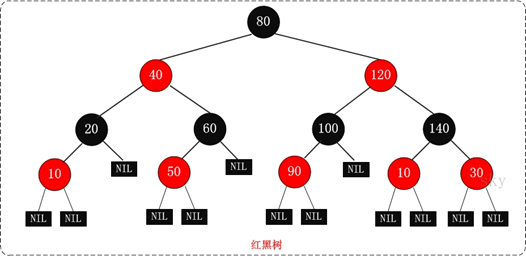
圖8 紅黑樹結構示意圖

那么將一個節點插入到紅黑樹中，需要執行哪些步驟呢？

將紅黑樹當做一棵二叉搜索樹，將節點插入；

將插入的節點著色為紅色；

通過一系列的旋轉和著色等操作，使之重新成為一棵紅黑樹。

在第二步中，被插入的節點被著為紅色之后，他會違背哪些特性呢

對于特性1，顯然是不會違背；

對于特性2，顯然也是不會違背；

對于特性4，顯然也是不會違背；

對于特性3，有可能會違背，我們將情況描述如下：

被插入的節點是根節點：直接把此節點涂為黑色；

被插入的節點的父節點是黑色：什么也不需要做。節點被插入后，仍然是紅黑樹；

被插入的節點的父節點是紅色：此種情況下與特性3違背，所以將情況分析如下：

當前節點的父節點是紅色，且當前節點的祖父節點的另一個子節點也是紅色。處理策略為：將父節點置為黑色、將叔叔節點置為黑色、將祖父節點置為紅色；

當前節點的父節點是紅色，叔叔節點時黑色，且當前節點是其父節點的右子節點。將父節點作為新的當前節點、以新的當前節點作為支點進行左旋；

當前節點的父節點是紅色，叔叔節點時黑色，且當前節點時父節點的左子節點。將父節點置為黑色、將祖父節點置為紅色、以祖父節點為支點進行右旋。

定理：一棵含有n個節點的紅黑樹的高度至多為2log(N+1)，證明過程請查看參考資料。

由此定理可推論紅黑樹的時間復雜度為log(N)；

·優缺點

優點：查詢效率高，插入和刪除的失衡的代銷比AVL要小很多。

缺點：紅黑樹不追求完全平衡。

·使用場景

紅黑樹的應用很廣泛，主要用來存儲有序的數據，時間復雜度為log(N)，效率非常高。例如java中的TreeSet、TreeMap、HashMap等。

4.2.3 B+Tree

·總述

提起B+Tree都會想到大名鼎鼎的MySql的InnoDB引擎，該引擎使用的數據結構就是B+Tree。B+Tree是B-Tree（平衡多路查找樹）的一種改良，使得更適合實現存儲索引結構，也是該篇分享中唯一一個與磁盤有關系的數據結構。首先我們先了解一下磁盤的相關東西。

系統從磁盤讀取數據到內存時是以磁盤塊（block）為基本單位，位于同一塊磁盤塊中的數據會被一次性讀取出來。InnoDB存儲引擎中有頁（Page）的概念，頁是引擎管理磁盤的基本單位。

·數據結構和算法

首先，先了解一下一棵m階B-Tree的特性：

每個節點最多有m個子節點；

除了根節點和葉子結點外，其他每個節點至少有m/2個子節點；

若根節點不是葉子節點，則至少有兩個子節點；

所有的葉子結點都是同一深度；

每個非葉子節點都包含n個關鍵字

關鍵字的個數的關系為 m/2-1 < n < m-1

B-Tree很適合作為搜索來使用，但是B-Tree有一個缺點就是針對范圍查找支持的不太友好，所以才有了B+Tree；

那么B+Tree的特性在B-Tree的基礎上又增加了如下幾點：

非葉子節點只存儲鍵值信息；

所有的葉子節點之間都有一個鏈指針（方便范圍查找）；

數據記錄都存放在葉子節點中；

將上述特點描述整理成下圖（假設一個頁（Page）只能寫四個數據）：

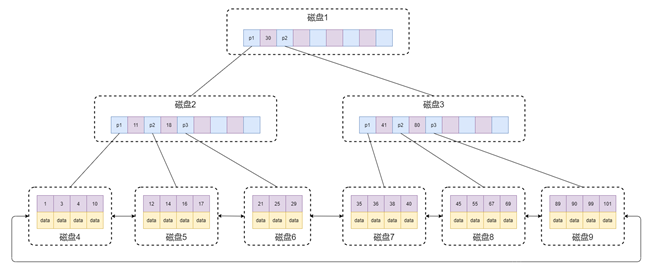
圖9B+Tree結構示意圖

這樣的數據結構可以進行兩種運算，一種是針對主鍵的范圍查找和分頁查找，另外一種是從根節點開始，進行隨機查找；

·優缺點

優點：利用磁盤可以存儲大量的數據，簡單的表結構在深度為3的B+Tree上可以保存大概上億條數據；B+Tree的深度大概也就是2~4，深度少就意味這IO會減少；B+Tree的時間復雜度log(m)N

缺點：插入或者刪除數據有可能會導致數據頁分裂；即使主鍵是遞增的也無法避免隨機寫，這點LSM-Tree很好的解決了；無法支持全文索引；

·使用場景

使用場景大多數數據庫的引擎，例如MySql,MongoDB等。

4.2.4 HashTree

·總述

HashTree是一種特殊的樹狀結構，根據質數分辨定理，樹每層的個數為1、2、3、5、7、11、13、17、19、23、29.....

·數據結構和算法

從2起的連續質數，連續10個質數接可以分辨大約6464693230個數，而按照目前CPU的計算水平，100次取余的整數除法操作幾乎不算什么難事。

我們選擇質數分辨算法來構建一顆哈希樹。選擇從2開始的連續質數來構建一個10層的哈希樹。第一層節點為根節點，根節點先有2個節點，第二層的每個節點包含3個子節點；以此類推，即每層節點的數據都是連續的質數。對質數進行取余操作得到的數據決定了處理的路徑。下面我們以隨機插入10個數（442 9041 3460 3164 2997 3663 8250 9088906 4005）為例，來圖解HashTree的插入過程，如下：

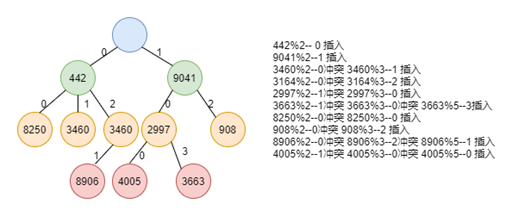
圖10HashTree構建過程示意圖

HashTree的節點查找過程和節點插入過程類似，就是對關鍵字用質數取余，根據余數確定下一節點的分叉路徑，知道找到目標節點。如上圖，在從對象中查找所匹配的對象，比較次數不超過10次，也就是說時間復雜度最多是o(1).

刪除的過程和查找類似。

·優缺點：

優點：結構簡單，查找迅速，結構不變。

缺點：非有序性。

4.2.5 其他數據結構

鑒于篇幅有限，余下重要數據結構將在下一篇文章中再來一起討論，敬請期待！

審核編輯：劉清