摘 要 ：目前在交通監(jiān)測領(lǐng)域中毫米波雷達(dá)和攝像頭已經(jīng)被大量使用，傳感器融合可以彌補(bǔ)單一傳感器的劣勢(shì)，做到優(yōu)勢(shì)互補(bǔ)，兩者融合需要標(biāo)定出傳感器間的空間轉(zhuǎn)換關(guān)系。對(duì)于毫米波雷達(dá)與攝像頭空間轉(zhuǎn)換關(guān)系已有文章提出一種基于單應(yīng)性變換原理的交通監(jiān)測毫米波雷達(dá)與攝像頭標(biāo)定方法，該方法只需提取交通監(jiān)測場景中目標(biāo)在兩傳感器中對(duì)應(yīng)的坐標(biāo)點(diǎn)對(duì)就能解算出傳感器間的轉(zhuǎn)換關(guān)系。相比傳統(tǒng)方法對(duì)攝像頭內(nèi)參數(shù)、傳感器自身以及傳感器之間的旋轉(zhuǎn)角度等參數(shù)進(jìn)行標(biāo)定，該方法更加簡潔有效，可以更高效的解決坐標(biāo)轉(zhuǎn)換問題，但目前還缺乏對(duì)影響單應(yīng)性標(biāo)定方法誤差因素的分析。針對(duì)這一問題，文中將通過實(shí)驗(yàn)對(duì)單應(yīng)性標(biāo)定方法中特征點(diǎn)空間分布以及數(shù)量對(duì)于標(biāo)定精確度的影響進(jìn)行研究并給出合適的標(biāo)定方案。

0 引 言

根據(jù)世界衛(wèi)生組織（World Health Organization, WHO）報(bào)告數(shù)據(jù) [1]，每年有大約 135 萬人死于道路交通事故，平均每 24 s 就有 1 人在道路上失去生命 ；道路交通傷害是 5 ～29 歲兒童和年輕人的主要死因，全球道路交通安全形勢(shì)嚴(yán)峻 [2-3]。交通事故的頻發(fā)給人們的生活健康和經(jīng)濟(jì)產(chǎn)生了巨大影響，所以優(yōu)良的交通監(jiān)測技術(shù)對(duì)人們的生活有著重大意義。目前在交通監(jiān)測領(lǐng)域，較為普遍的是使用單一光學(xué)攝像頭對(duì)車輛進(jìn)行識(shí)別跟蹤或者使用雷達(dá)對(duì)車輛進(jìn)行測速測距。但是這些傳統(tǒng)的監(jiān)控方式都存在一定的局限性，光學(xué)攝像頭可以獲得較為豐富的目標(biāo)及場景的紋理特征，但其測速測距能力較弱，且光學(xué)傳感器容易受到天氣、光照等因素的影響。而毫米波雷達(dá)在測速測距以及抗天氣干擾等方面具有天然的優(yōu)勢(shì)，但卻無法獲得目標(biāo)的紋理信息等特征。將光學(xué)攝像頭與毫米波雷達(dá)傳感器進(jìn)行融合可以做到優(yōu)勢(shì)互補(bǔ)。因此，光學(xué)攝像頭與毫米波雷達(dá)信息的融合已成為智能交通系統(tǒng)的研究熱點(diǎn) [4]。

在進(jìn)行傳感器數(shù)據(jù)融合之前，首先要通過傳感器標(biāo)定來解決毫米波雷達(dá)與光學(xué)攝像頭間的空間轉(zhuǎn)換問題。目前已經(jīng)有學(xué)者研究出了一些較為有效的毫米波雷達(dá)與光學(xué)攝像頭標(biāo)定方法。日本豐巴技術(shù)中心研究人員研發(fā)出了基于毫米波雷達(dá)和攝像頭的障礙物檢測分類系統(tǒng)，首先利用攝像頭獲取圖像，使用毫米波雷達(dá)選出并建立感興趣區(qū)域，然后利用神經(jīng)網(wǎng)絡(luò)進(jìn)行待測車輛識(shí)別，但這種方法識(shí)別效果的精確性較差[5]。Nabati，Ramin & Qi[6] 等提出了一種中心融合的深度學(xué)習(xí)網(wǎng)絡(luò)，實(shí)現(xiàn)了雷達(dá)與攝像頭的融合，該方法為車輛檢測建立了立體的視錐而不再是檢測框，從而提高了自動(dòng)駕駛過程中2 個(gè)傳感器標(biāo)定及融合的準(zhǔn)確性。張富有 [7] 提出一種通過標(biāo)定攝像頭內(nèi)參數(shù)以及毫米波雷達(dá)與光學(xué)攝像頭三軸旋轉(zhuǎn)自由度的方法來解算空間轉(zhuǎn)換關(guān)系，從而實(shí)現(xiàn)傳感器間的標(biāo)定。但這種方式需要標(biāo)定的參數(shù)過多，增加了實(shí)驗(yàn)難度，并且攝像頭標(biāo)定誤差也會(huì)受多種因素影響 [8-9]。已有文章提出一種基于單應(yīng)性變換的毫米波雷達(dá)與攝像頭標(biāo)定方法，該方法通過在毫米波雷達(dá)與攝像頭共同采集區(qū)域中設(shè)置定標(biāo)物，然后提取定標(biāo)物在雷達(dá)數(shù)據(jù)以及攝像頭像素?cái)?shù)據(jù)中的坐標(biāo)形成特征點(diǎn)對(duì)，通過多個(gè)特征點(diǎn)對(duì)可以標(biāo)定出兩者的空間轉(zhuǎn)換關(guān)系。但基于單應(yīng)性變換的毫米波雷達(dá)與攝像頭標(biāo)定方法缺少對(duì)影響標(biāo)定誤差的因素的分析。

基于單應(yīng)性變換的毫米波雷達(dá)與攝像頭標(biāo)定方法缺少對(duì)影響誤差因素的分析，本文將通過實(shí)驗(yàn)從特征點(diǎn)空間分布以及數(shù)量對(duì)單應(yīng)性標(biāo)定誤差的影響進(jìn)行分析。

1 單應(yīng)性標(biāo)定原理及誤差建模

1.1 毫米波雷達(dá)與攝像頭單應(yīng)性標(biāo)定原理介紹

單應(yīng)性變換原理常被應(yīng)用于圖像領(lǐng)域，比如相機(jī)成像可以把現(xiàn)實(shí)世界中的三維目標(biāo)表示在二維的像素平面中。由此單應(yīng)性變換可以用來表示三維目標(biāo)點(diǎn)與二維目標(biāo)點(diǎn)之間的映射關(guān)系 [10]。毫米波雷達(dá)采集的目標(biāo)數(shù)據(jù)為二維坐標(biāo) (xr, yr)，而攝像機(jī)采集的目標(biāo)像素點(diǎn)坐標(biāo)為 (u, v)，假設(shè)雷達(dá)檢測到的目標(biāo)以及攝像機(jī)檢測到的目標(biāo)全部在雷達(dá)采集平面 xroryr與像素平面 ucocvc 上，如圖 1 所示。

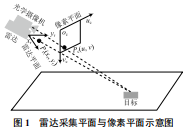
圖 1 所示為一個(gè)在毫米波雷達(dá)與攝像頭公共視場內(nèi)的目標(biāo)，假設(shè)其在毫米波雷達(dá)坐標(biāo)下的位置為 Pr(xr, yr)，在攝像機(jī)像素坐標(biāo)系中的位置為 Pc(u, v)。由單應(yīng)性變換原理可知，標(biāo)定雷達(dá)采集的目標(biāo)點(diǎn)與攝像機(jī)像素坐標(biāo)之間的空間轉(zhuǎn)換關(guān)系就是標(biāo)定雷達(dá)采集平面 xroryr 與像素平面 ucocvc 之間的映射關(guān)系，根據(jù)單應(yīng)性原理可得雷達(dá)采集平面與圖像像素平面關(guān)系 ：

式中，H 為雷達(dá)平面與像素平面之間的單應(yīng)性矩陣，其表示兩個(gè)采集面之間的轉(zhuǎn)換關(guān)系，H 是一個(gè) 3×3 的矩陣，s 為常數(shù)。雷達(dá)采集平面和像素平面之間的關(guān)系可以通過估計(jì)單應(yīng)性矩陣 H 得到，此過程不需要對(duì)攝像機(jī)內(nèi)外參數(shù)等進(jìn)行單獨(dú)標(biāo)定，也不需要對(duì)各坐標(biāo)軸旋轉(zhuǎn)角度進(jìn)行標(biāo)定。根據(jù)式（1）將單應(yīng)性矩陣展開可得：

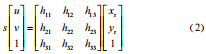
將式（2）展開可以得到 ：

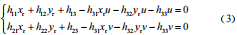
在雷達(dá)平面與像素平面取 N 個(gè)對(duì)應(yīng)的目標(biāo)點(diǎn)對(duì)，帶入式（3）化為矩陣則有 ：

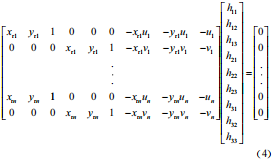
式（4）左矩陣為 2N×9 階的矩陣，右部分矩陣為 9×1 階的矩陣，記為單應(yīng)性矩陣 H。最小需要 4 個(gè)不共線的特征點(diǎn)對(duì)可以求解出單應(yīng)性矩陣，并且對(duì)于超定方程組，可以通過最小二乘法求解，但為了減少數(shù)據(jù)中噪聲對(duì)單應(yīng)性矩陣標(biāo)定的影響，采用最小中值估計(jì)的方法來增加 H 的準(zhǔn)確性和魯棒性。定義每個(gè)標(biāo)定出的單應(yīng)性矩陣 H 的標(biāo)定誤差為：

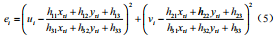
最小中值優(yōu)化估計(jì)實(shí)現(xiàn)步驟如下 ：

（1）對(duì)于包含 N 對(duì)特征點(diǎn)的集合，每次隨機(jī)抽取 4 個(gè)特征點(diǎn)對(duì)組成一個(gè)集合 ；

（2）對(duì)于每一個(gè)樣本集，使用最小二乘法估計(jì)得到一個(gè)單應(yīng)性矩陣 hi ；

（3）對(duì)于每一個(gè) hi，可以求出整個(gè)數(shù)據(jù)集所有點(diǎn)對(duì)的標(biāo)定誤差 ei，再找出 ei 的中值 emedi ；

（4）求解出使 emedi 最小的 hi。通過上述方法可以求解出毫米波雷達(dá)與攝像頭之間的單應(yīng)性矩陣，只需采集一定數(shù)量的定標(biāo)物特征點(diǎn)對(duì)就可以完成毫米波雷達(dá)與攝像頭之間的標(biāo)定，實(shí)現(xiàn)毫米波雷達(dá)坐標(biāo)與像素坐標(biāo)之間的轉(zhuǎn)換。

1.2 誤差因素建模

根據(jù)式（2）可知，單應(yīng)性標(biāo)定法中如果獲得一定數(shù)量的特征點(diǎn)對(duì)，即成對(duì)的 (xr, yr) 與 (uc, vc) 就可以求解出單應(yīng)性矩陣，并且由于單應(yīng)性矩陣實(shí)際是一種超定方程組，因此求解至少需要 4 對(duì)特征點(diǎn)對(duì)。但是特征點(diǎn)對(duì)的數(shù)量選擇多少以及特征點(diǎn)對(duì)選取的位置對(duì)標(biāo)定精度產(chǎn)生的影響需要進(jìn)一步實(shí)驗(yàn)探究。針對(duì)單應(yīng)性變換標(biāo)定方法將其標(biāo)定誤差與其影響因素定義如式（6）所示 ：

式中：etotal 表示標(biāo)定的總誤差；r 為雷達(dá)自身采集誤差；l 為特征點(diǎn)空間分布的位置；n 為特征點(diǎn)數(shù)量。公式說明標(biāo)定總誤差為3 個(gè)誤差因素共同作用下產(chǎn)生的結(jié)果。在這 3 個(gè)誤差因素中，雷達(dá)采集誤差受雷達(dá)硬件自身測距精度與測角精度的影響，因設(shè)備差異的不同會(huì)導(dǎo)致不同測距測角精度誤差。

2 實(shí)驗(yàn)分析

2.1實(shí)驗(yàn)設(shè)備介紹

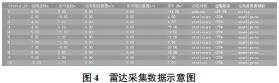
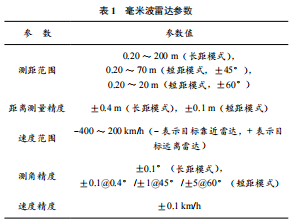
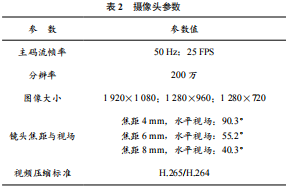
本文采用的實(shí)驗(yàn)設(shè)備為77G 大陸 ARS408 毫米波雷達(dá)以及海康威視光學(xué)監(jiān)控?cái)z像頭，設(shè)備如圖2 所示，雷達(dá)采集界面示意圖如圖3 所示，雷達(dá)采集數(shù)據(jù)示意圖如圖4所示。毫米波雷達(dá)參數(shù)見表1 所列，攝像頭參數(shù)見表2 所列。

2.2 誤差實(shí)驗(yàn)分析

在本節(jié)將對(duì)提出的標(biāo)定模型中各因素進(jìn)行實(shí)驗(yàn)分析，研究特征點(diǎn)對(duì)空間位置分布以及特征點(diǎn)對(duì)數(shù)量對(duì)標(biāo)定精度的影響。設(shè)計(jì)實(shí)驗(yàn)在操場上利用攝像頭與毫米波雷達(dá)對(duì)不同位置的角反射器進(jìn)行采集。雷達(dá)采集數(shù)據(jù)包含縱向距離 xr，橫向距離 yr，縱向速度 vx，橫向速度 vy 以及 RCS 等信息。攝像頭采集的數(shù)據(jù)中，角反射器的位置為像素坐標(biāo) (uf, vf)。本次實(shí)驗(yàn)將在毫米波雷達(dá)與攝像頭的公共采集視場中放置角反射器，每一個(gè)角反射器都可以從雷達(dá)數(shù)據(jù)中提取出其坐標(biāo)位置(xr, yr) 以及其在攝像頭數(shù)據(jù)中的像素坐標(biāo) (uf, vf)，由此形成一組特征點(diǎn)對(duì)，通過不斷改變角反射器的位置從而獲得不同的特征點(diǎn)對(duì)。

2.2.1 雷達(dá)設(shè)備采集誤差

由于毫米波雷達(dá)設(shè)備硬件本身在測速和測角方面存在一定的誤差，這也會(huì)給單應(yīng)性變換標(biāo)定帶來一定的誤差。根據(jù)表 1 所列的毫米波雷達(dá)參數(shù)，可以制作圖 5 所示的毫米波雷達(dá)設(shè)備采集誤差模型。

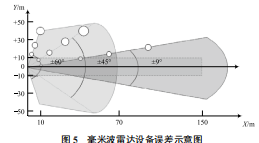
圖 5 中，紅色區(qū)域代表雷達(dá)遠(yuǎn)距離掃描模式，藍(lán)色區(qū)域代表近距離掃描模式，白色圓圈代表此處目標(biāo)的位置測量誤差，圓圈的半徑越大代表誤差越大。根據(jù)此圖可知，目標(biāo)距離雷達(dá)越遠(yuǎn)相對(duì)角度越大，位置測量精度會(huì)增大，故綠色區(qū)域?yàn)檩^為合適的采集區(qū)域。實(shí)驗(yàn)根據(jù)雷達(dá)誤差模型選擇雷達(dá)縱向 50 m 以內(nèi)，橫向 ±10 m 內(nèi)的范圍作為實(shí)驗(yàn)區(qū)域，以降低雷達(dá)設(shè)備誤差對(duì)標(biāo)定精度的影響。

2.2.2 特征點(diǎn)空間位置構(gòu)型實(shí)驗(yàn)

標(biāo)定誤差模型 etotal=f(r, l, n) 受雷達(dá)設(shè)備誤差、特征點(diǎn)空間分布，以及特征點(diǎn)數(shù)量的綜合影響，由于求解單應(yīng)性變換矩陣最少需要 4 組點(diǎn)對(duì)并且不能共線，所以采用控制變量的方式研究特征點(diǎn)數(shù)為 4 對(duì)情況下，不同空間構(gòu)型對(duì)標(biāo)定誤差的影響。定義兩種主要的空間構(gòu)型如圖 6、圖 7所示。

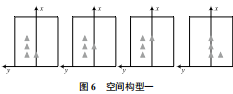
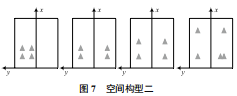
由于 4 點(diǎn)不共線主要考慮空間構(gòu)型一與空間構(gòu)型二這兩種位置分布，其他位置分布可以通過整體旋轉(zhuǎn)、平移與這兩種空間構(gòu)型進(jìn)行等效。實(shí)驗(yàn)采集一定組數(shù)的空間構(gòu)型一與空間構(gòu)型二的定標(biāo)物雷達(dá)坐標(biāo)數(shù)據(jù) (xr, yr)，通對(duì)標(biāo)定誤差進(jìn)行計(jì)算，將數(shù)據(jù)記錄在表 3 與表 4。

兩種構(gòu)型標(biāo)定誤差如圖 8 所示。

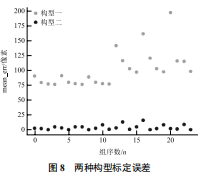
由圖中的構(gòu)型數(shù)據(jù)與誤差的關(guān)系可知，空間構(gòu)型二的特征點(diǎn)位置分布比構(gòu)型一所示的空間分布標(biāo)定誤差更小。并且對(duì)表 4 中構(gòu)型二數(shù)據(jù)進(jìn)行分析可知，對(duì)于空間構(gòu)型二的位置分布，當(dāng) 4 個(gè)點(diǎn)空間差異越大即 4 個(gè)點(diǎn)在橫向和縱向距離增大時(shí)標(biāo)定誤差會(huì)下降。

2.2.3 特征點(diǎn)數(shù)量實(shí)驗(yàn)分析

通過實(shí)驗(yàn)分析了空間構(gòu)型對(duì)單應(yīng)性變換標(biāo)定誤差的影響，證明了空間構(gòu)型二比空間構(gòu)型一的標(biāo)定誤差小，本節(jié)選擇空間構(gòu)型二作為特征點(diǎn)分布，保持構(gòu)型不變的情況下研究特征點(diǎn)數(shù)量對(duì)單應(yīng)性標(biāo)定誤差的影響。特征點(diǎn)位置實(shí)驗(yàn)數(shù)據(jù)(xr, yr) 為（11.2，2.5），（14，2.5），（18.2，-4.7），（24，-4.7）（17，2.5），（30，-4.7），（20，2.5），（36，-4.7），表 5 為不同特征點(diǎn)數(shù)量的標(biāo)定誤差數(shù)據(jù)。

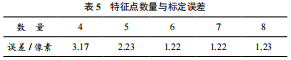
通過表中的數(shù)據(jù)可以看出，在同一種空間構(gòu)型下，隨著特征點(diǎn)數(shù)量單應(yīng)性標(biāo)定誤差逐漸下降，當(dāng)點(diǎn)數(shù)增加到 6 個(gè)點(diǎn)時(shí)，標(biāo)定誤差已經(jīng)基本不發(fā)生變化。所以在標(biāo)定時(shí)選擇 6 個(gè)點(diǎn)較為合適。

3 結(jié) 語

本文研究了毫米波雷達(dá)與攝像頭單應(yīng)性變換標(biāo)定方法中誤差因素對(duì)單應(yīng)性變換標(biāo)定精度的影響。建立了誤差模型并分別對(duì)毫米波雷達(dá)設(shè)備誤差、特征點(diǎn)空間位置構(gòu)型、特征點(diǎn)數(shù)量這三個(gè)因素對(duì)標(biāo)定精度的影響進(jìn)行了實(shí)驗(yàn)分析。結(jié)果表明，文中的空間構(gòu)型二特征點(diǎn)位置分布的標(biāo)定誤差較小，并且在空間構(gòu)型二下，特征點(diǎn)數(shù)量選擇 6 點(diǎn)標(biāo)定誤差可達(dá)到最小并且基本不再變化。本文的結(jié)果為后續(xù)毫米波雷達(dá)與攝像頭標(biāo)定實(shí)驗(yàn)方案的設(shè)計(jì)提供了基礎(chǔ)，具有一定的研究意義。

審核編輯：湯梓紅