摘要

因果特征選擇算法(也稱為馬爾科夫邊界發(fā)現(xiàn))學習目標變量的馬爾科夫邊界,選擇與目標存在因果關系的特征,具有比傳統(tǒng)方法更好的可解釋性和魯棒性.文中對現(xiàn)有因果特征選擇算法進行全面綜述,分為單重馬爾科夫邊界發(fā)現(xiàn)算法和多重馬爾科夫邊界發(fā)現(xiàn)算法.基于每類算法的發(fā)展歷程,詳細介紹每類的經典算法和研究進展,對比它們在準確性、效率、數(shù)據(jù)依賴性等方面的優(yōu)劣.此外,進一步總結因果特征選擇在特殊數(shù)據(jù)(半監(jiān)督數(shù)據(jù)、多標簽數(shù)據(jù)、多源數(shù)據(jù)、流數(shù)據(jù)等)中的改進和應用.最后,分析該領域的當前研究熱點和未來發(fā)展趨勢,并建立因果特征選擇資料庫,匯總該領域常用的算法包和數(shù)據(jù)集.

高維數(shù)據(jù)為真實世界的機器學習任務帶來諸多挑戰(zhàn), 如計算資源和存儲資源的消耗、數(shù)據(jù)的過擬合, 學習算法的性能退化[1], 而最具判別性的信息僅被一部分相關特征攜帶[2].為了降低數(shù)據(jù)維度, 避免維度災難, 特征選擇研究受到廣泛關注.大量的實證研究[3, 4, 5]表明, 對于多數(shù)涉及數(shù)據(jù)擬合或統(tǒng)計分類的機器學習算法, 在去除不相關特征和冗余特征的特征子集上, 通常能獲得比在原始特征集合上更好的擬合度或分類精度.此外, 選擇更小的特征子集有助于更好地理解底層的數(shù)據(jù)生成流程[6].

傳統(tǒng)的特征選擇算法主要分為封裝法、過濾法和嵌入法三類[7].封裝法[8]為不同的特征子集訓練一個學習器, 評估其在該特征子集上的表現(xiàn), 決定所選特征子集.過濾法[9]使用一個評估函數(shù), 為特征評分并選擇分數(shù)較高的特征, 因此不依賴額外的分類器, 更高效.嵌入法[10]將特征選擇過程嵌入學習過程中, 同時搜索特征選擇空間和學習器參數(shù)空間, 獲得特征子集.

傳統(tǒng)的特征選擇算法根據(jù)特征和目標變量之間的相關性尋找相關特征子集[11].然而, 相關關系只能反映目標變量和特征之間的共存關系, 而無法解釋決定目標變量取值的潛在機制[12, 13].一些研究表明[12, 13], 因果關系具有更好的可解釋性和魯棒性.例如, 將吸煙與肺癌患者數(shù)據(jù)集上“ 肺癌” (例子中變量取值均為“ 是” 、“ 否” )作為目標變量, “ 黃手指” 和“ 吸煙” 作為特征變量.由于“ 吸煙” 可用來解釋“ 肺癌” , 而長期吸煙手指會受到焦油的污染, 因此“ 黃手指” 和“ 吸煙” 與“ 肺癌” 之間存在相關關系, 而只有“ 吸煙” 與“ 肺癌” 之間存在因果關系.當一些吸煙者為了隱藏吸煙習慣而去除手指上的黃漬時, 基于“ 黃手指” 的預測模型將失效, 而基于“ 吸煙” 的預測模型更魯棒.

為了尋找更魯棒的因果特征, 近年來, 因果特征選擇算法被廣泛研究.該類算法通過學習目標變量的馬爾科夫邊界(Markov Boundary, MB)[14]以尋找關鍵特征, 因此又被稱為MB發(fā)現(xiàn)算法.具體地, MB的概念來源于因果貝葉斯網絡, 在滿足忠實性假設的貝葉斯網絡中, 一個變量的MB集合是唯一的, 包含該目標變量的父節(jié)點、子節(jié)點及配偶節(jié)點(子節(jié)點的其它父節(jié)點)[14].因此, MB反映目標變量周圍的局部因果關系, 給定目標變量的MB作為條件集合, 其它特征條件獨立于目標變量[14].基于此屬性:Tsamardinos等[15]證明在分類問題中, 類別變量的MB是具有最大預測性的最小特征子集; Pellet等[16]證明類別變量的MB集合是特征選擇的最優(yōu)解.因此, 因果特征選擇算法通常具有可靠的理論保證.

作為一種算法思路, 基于因果關系的特征選擇算法促進特征選擇的可解釋性和魯棒性.近年來, 因果特征選擇算法不斷發(fā)展, 不僅提升單/多重馬爾科夫邊界發(fā)現(xiàn)算法的搜索精度和計算效率, 在半監(jiān)督數(shù)據(jù)、流數(shù)據(jù)、多源數(shù)據(jù)、多標簽數(shù)據(jù)等特殊場景下也不斷發(fā)展.這些算法無需學習包含所有特征的完整貝葉斯網絡結構, 即可挖掘目標變量周圍的因果特征.本文對現(xiàn)有因果特征選擇方法進行較全面的研究和綜述.

基于原理與現(xiàn)有方法分類

1.問題定義與基礎理論

本節(jié)介紹MB相關的基本定義和基礎理論.本文使用U表示特征集合, T表示目標變量(標簽).MB的概念來源于人工智能基礎模型之一的貝葉斯網絡.

定義 1 貝葉斯網絡[14] 對于三元組< U, G, P> , U表示變量集合, G表示U上的有向無環(huán)圖(Directed Acyclic Graph, DAG), P表示U上的概率分布.對于? X∈ U, 將X在G中的父變量作為條件集合, 如果任意X的非后代變量在P中都條件獨立于X, 那么< U, G, P> 為貝葉斯網絡.

貝葉斯網絡表征一個變量集合中的因果關系.在有向無環(huán)圖中, 對于一對直接相連的父子變量, 父變量是子變量的直接原因, 子變量是父變量的直接結果[14].忠實性是貝葉斯網絡的基礎假設之一, 定義如下.

定義 2 忠實性[14] 給定貝葉斯網絡< U, G, P> , G忠實于P當且僅當P中的每個條件獨立性關系都是由G和馬爾科夫條件決定的.P忠實于G當且僅當存在一個G的子圖忠實于P.

MB的概念是基于忠實的貝葉斯網絡而提出的, 定義如下.

定義 3 馬爾科夫邊界[14] 在滿足忠實性的貝葉斯網絡中, 一個節(jié)點的馬爾科夫邊界包含該節(jié)點的父節(jié)點、子節(jié)點和配偶節(jié)點(子節(jié)點的其它父節(jié)點)[14].

根據(jù)定義3, 一個節(jié)點的MB可直接從忠實的貝葉斯網絡中“ 讀” 出來.如圖1所示, 節(jié)點T的MB為{A, B, G, H, F}, 包含父節(jié)點A、B, 子節(jié)點G、H, 配偶節(jié)點F.從因果圖的角度分析, MB提供變量周圍的局部因果結構, 父節(jié)點、子節(jié)點、配偶節(jié)點分別對應目標變量的直接原因、直接結果、直接結果的其它原因.MB發(fā)現(xiàn)算法通過挖掘變量的局部因果結構, 無需學習完整的貝葉斯網絡即可找到變量的MB.而變量的MB集合有一個特殊的統(tǒng)計特性, 見定理1.

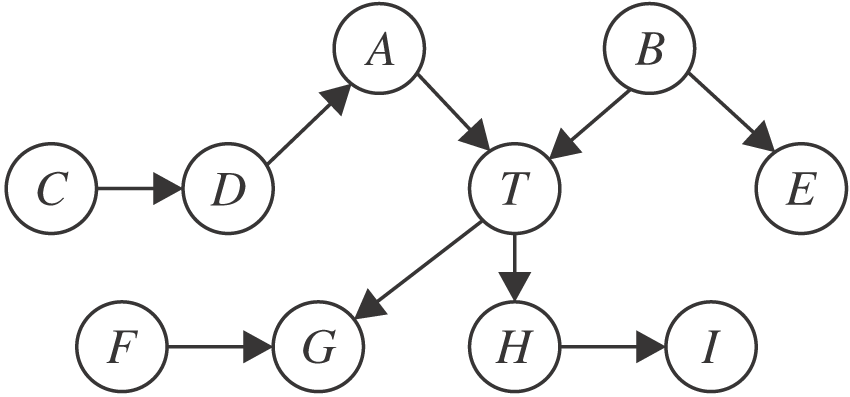
圖1 馬爾科夫邊界的例子

Fig.1 An example of Markov boundary

定理 1 對于變量X∈ U, X的馬爾科夫邊界MB?U, 滿足:? Y∈ U-MB-{X}, X⊥Y| MB, 且MB為滿足該統(tǒng)計特性的最小變量集.

定理1 中闡述MB的最小性, MB的超集通常稱為馬爾科夫毯(Markov Blanket).根據(jù)定理1, 以MB集合為條件, 目標變量會條件獨立于其它特征.因此, MB中的特征攜帶所有關于目標變量的預測信息, 并且其“ 最小性” 保證MB可作為特征選擇問題的最優(yōu)解, 見定理2.

定理 2 在滿足忠實性假設的數(shù)據(jù)中, 目標變量的MB是唯一的, 并且為特征選擇的最優(yōu)解[15, 16].

定理2 為MB發(fā)現(xiàn)算法解決特征選擇問題提供理論保證, 由于MB發(fā)現(xiàn)算法根據(jù)數(shù)據(jù)中的因果關系選擇特征, 并且特征包含目標變量的因果信息, 因此使用MB發(fā)現(xiàn)算法選擇特征的過程稱為因果特征選擇.

2.現(xiàn)有馬爾科夫邊界學習方法分類及其基本原理

圖2給出本文對現(xiàn)有MB發(fā)現(xiàn)算法的分類.常規(guī)數(shù)據(jù)中的MB發(fā)現(xiàn)算法主要分為單重MB發(fā)現(xiàn)算法和多重MB發(fā)現(xiàn)算法, 這兩類算法的應用場景取決于訓練數(shù)據(jù)是否滿足忠實性假設.根據(jù)定理2, 在滿足忠實性的條件下, 目標變量的MB是唯一的, 當真實數(shù)據(jù)并不完全滿足忠實性條件時, 目標變量可能存在多個等價的MB.因此, 一部分現(xiàn)有算法假設數(shù)據(jù)滿足忠實性, 并且試圖尋找目標變量的唯一MB, 該類算法稱為單重MB發(fā)現(xiàn)算法.另一部分算法考慮忠實性假設被違反的情況, 這些算法可挖掘目標變量的多個等價MB, 該類算法稱為多重MB發(fā)現(xiàn)算法.特殊數(shù)據(jù)中的MB發(fā)現(xiàn)算法作為一類單獨介紹, 其中包括半監(jiān)督數(shù)據(jù)MB發(fā)現(xiàn)算法、流數(shù)據(jù)MB發(fā)現(xiàn)算法、多源數(shù)據(jù)MB發(fā)現(xiàn)算法、多標簽數(shù)據(jù)MB發(fā)現(xiàn)算法.本文按照上述分類介紹現(xiàn)有算法的特點.

圖2 現(xiàn)有MB發(fā)現(xiàn)算法的分類

Fig.2 Categories of existing MB discovery algorithms

單重MB發(fā)現(xiàn)算法假設目標變量有唯一的MB, 輸出的MB集合可直接作為特征選擇的結果.該類算法主要分為兩類:直接的MB發(fā)現(xiàn)算法(直接法)和分治的MB發(fā)現(xiàn)算法(分治法).主要區(qū)別是:直接法根據(jù)MB的性質(定理1)直接學習MB變量, 而分治法分別學習父子變量和配偶變量.主要理論依據(jù)為定理3和定理4.

定理 3 在U上的貝葉斯網絡中, 如果節(jié)點X和Y滿足:任意變量子集Z?U-{X, Y}, X⊥Y|Z不成立, 那么X和Y是一對父子變量[17].

定理 4 在U上的貝葉斯網絡中, 如果不相連的節(jié)點X和Y均與T相連, 如果存在變量子集Z?U-{X, Y, T}, 使得X⊥Y|Z成立但X⊥Y|Z∪ {T}不成立, 那么X和Y是一對配偶變量[17].

定理3和定理4分別給出父子變量和配偶變量的判別條件, 基于上述定理, 分治的MB發(fā)現(xiàn)算法可通過條件獨立性測試分別搜索父子和配偶變量.

如圖3所示, 單重MB發(fā)現(xiàn)算法通常使用增長階段和收縮階段搜索MB變量或父子變量.增長階段用于識別并添加可能的真變量, 而收縮階段檢測并刪除增長步驟中找到的假變量.基于這一框架, 分治法需要進一步搜索配偶變量.直接法通常在時間效率上更優(yōu).但由于分治法在條件獨立性測試中使用規(guī)模更小的條件集合, 因此通常分治法可達到比直接法更高的準確性.

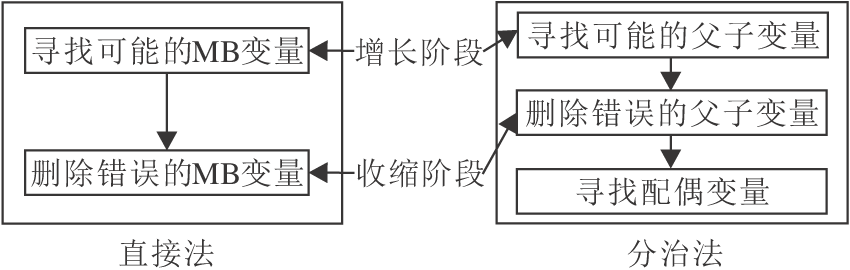
圖3 直接法和分治法的區(qū)別

Fig.3 Difference between direct methods and divide-and-conquer methods

可用于MB發(fā)現(xiàn)算法的通用條件獨立性測試方法有5種:1)λ 2測試、G2測試、互信息計算, 可用于離散數(shù)據(jù)[18]; 2)菲爾遜Z檢驗[19], 可用于帶有高斯誤差的線性關系的連續(xù)數(shù)據(jù); 3)基于核的條件獨立性測試方法[20], 可用于非線性、非高斯噪聲的連續(xù)數(shù)據(jù).

多重MB發(fā)現(xiàn)算法研究忠實性假設被違反的情況下一個變量的多個等價MB.理論上來說, 目標變量的多重MB攜帶等價的信息且具有相似的預測能力[21], 該類算法存在的意義是:1)由于實際應用中多個等價的MB適應的特定學習模型是不同的, 多重MB可用于解釋學習模型的多樣性現(xiàn)象; 2)實際應用中可能存在多個等價的MB, 但并非所有MB都適合作為特征子集建立學習模型.例如, 當不同變量的獲取成本可能不同時, 多重MB算法可用于探索較低獲取成本但具有相似預測性的替代解決方案(特征子集).

根據(jù)Statnikov等[21]的研究, 多重MB的本質原因是等價信息現(xiàn)象, 定義4和定理5如下.

定義 4 等價信息[21] 對變量集合X?U, Y?U及目標變量T∈ U, X和Y包含T的等價信息當且僅當X和Y與T相關且滿足X⊥T|Y, Y⊥T|X.

定理 5 當且僅當沒有發(fā)生信息等價時, 目標變量有一個唯一的MB集合[21].

根據(jù)定理5, 多重MB與等價信息現(xiàn)象是共存的, 因此尋找多個MB的過程也就是識別等價信息的過程[21].現(xiàn)有的多重MB發(fā)現(xiàn)算法通常遵循如下步驟:1)使用單重MB發(fā)現(xiàn)算法找到一個初始的MB; 2)在當前MB中選擇特征子集, 將其從源數(shù)據(jù)分布中移除, 再在新的數(shù)據(jù)分布中找到新的MB; 3)測試新MB是否正確.

特殊數(shù)據(jù)的MB發(fā)現(xiàn)算法主要是面向近年來逐漸流行的一些特殊學習場景, 根據(jù)本文的調研, 目前主要包括但不限于:半監(jiān)督數(shù)據(jù)MB發(fā)現(xiàn)算法、多標簽數(shù)據(jù)MB發(fā)現(xiàn)算法、多源數(shù)據(jù)MB發(fā)現(xiàn)算法和流數(shù)據(jù)MB發(fā)現(xiàn)算法.這些算法大多對應某個單重MB發(fā)現(xiàn)算法, 考慮對應場景的特點, 將單重MB算法擴展應用到特殊數(shù)據(jù)中.

審核編輯：湯梓紅