Minitab中的正態性檢驗提供了三種方法:Anderson-Darling(AD),Ryan-Joiner(RJ)和Kolmogorov-Smirnov(KS)。AD檢驗是默認的,那它在檢驗非正態的時候是不是最好的方法呢?
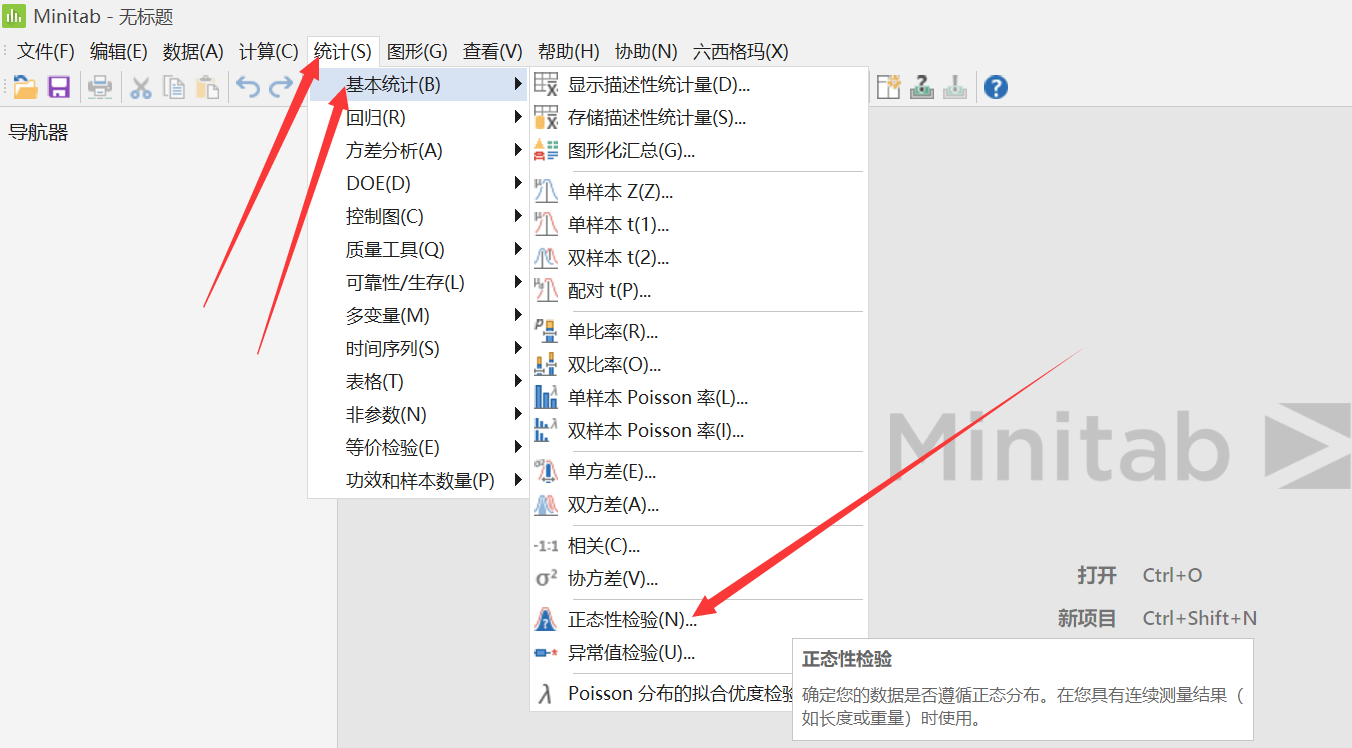
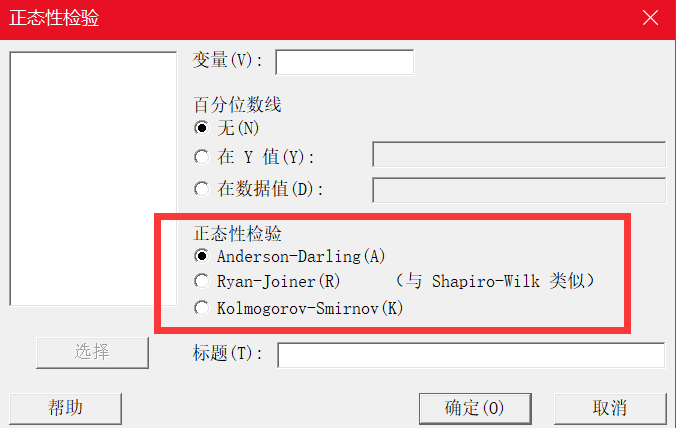
對于這三種正態性檢驗方法,檢驗結果有時是有差異的(如下圖),那么就有個問題:到底以哪種方法的結果為準?
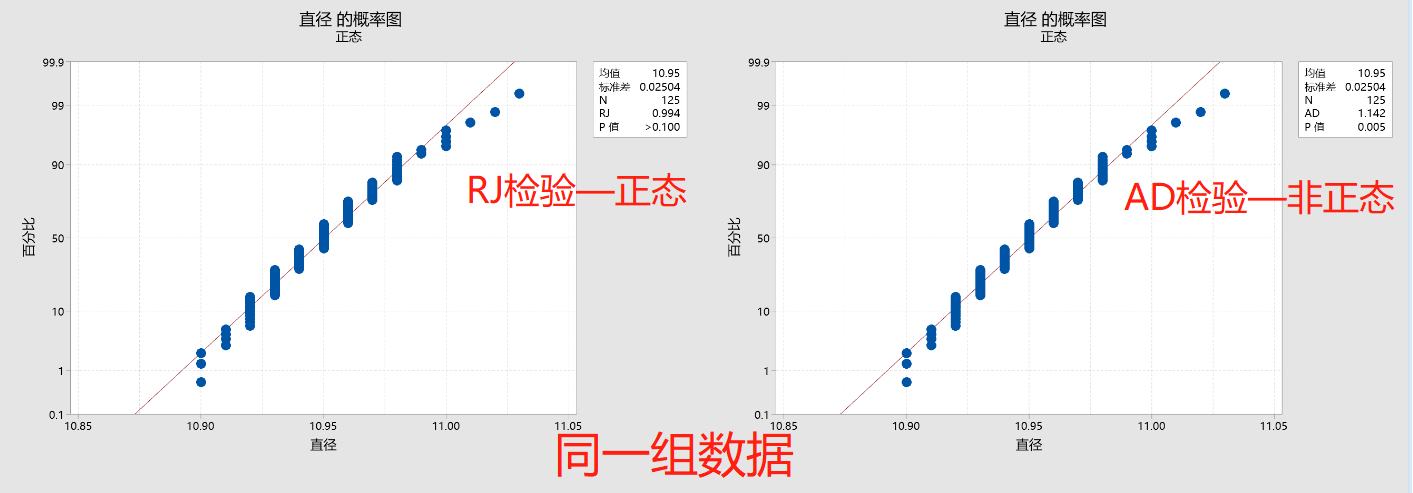
今天我們就來比較一下每種正態性檢驗在以下三種不同情形下檢驗非正態數據的能力。我們將為每個情形使用模擬數據,但是它們反映了在分析數據以提高質量時可能遇到的常見情況。
三種情形
情形1:生產過程中產生較大的離群值。
在此模擬中,從平均值= 0,標準偏差= 1的正態分布中模擬了29個值,從均值= 0,標準偏差= 4的正態分布中模擬了1個值。
情形2:制造過程發生了變化,從而導致分布發生變化。
創建一個雙峰分布(如下圖),一個是均值為10,標準差為1的正態分布;一個是均值為14,標準差為1的正態分布。
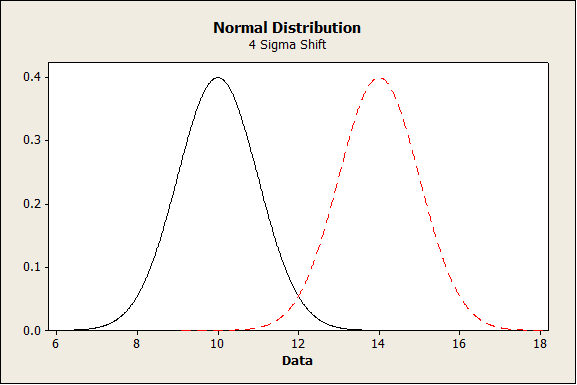
情形3:測量結果自然遵循非正態分布,正如我們通常會看到的失效時間數據。對于這種情況,從Weibull(a = 1,b = 1.5)分布中模擬了30個值。
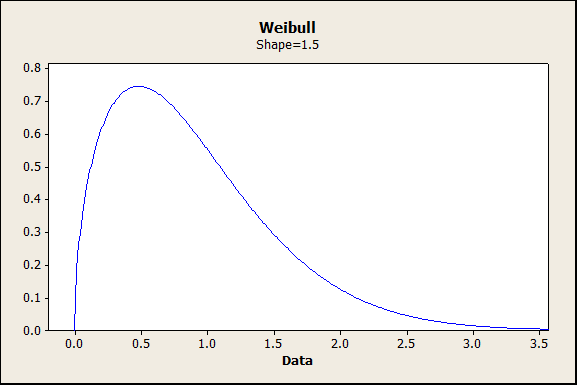
注意:此文中評估的三種情形并非旨在評估使用中心極限定理的檢驗(例如單樣本t,雙樣本t和配對t檢驗)的正態性假設的有效性。我們的重點是在使用分布估計制造有缺陷(不合格)單元的可能性時檢驗非正態性。
仿真(情形1為例)
步驟1:模擬數據(即29個來自正態分布+ 1個來自具有大標準差的正態分布)。
步驟2:運行正態性檢驗(AD,RJ和KS),并記錄P值。
步驟3:重復步驟1和2 ,N次。
步驟4:分析每個正態性檢驗的P值,并基于不同的alpha值繪制拒絕正態性概率的置信區間。
仿真結果比較
在情形1中,Ryan-Joiner檢驗顯然是贏家,仿真結果如下。
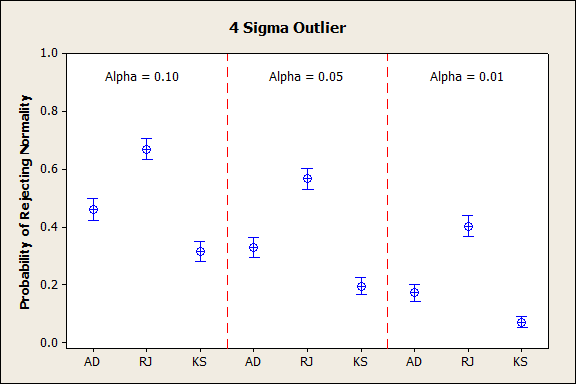
在情形2中,Anderson-Darling檢驗是最好的,仿真結果如下。

在情形3中,AD和RJ檢驗之間沒有太大差異。兩者都比Kolmogorov-Smirnov檢驗更有效地檢驗非正態性,仿真結果如下。
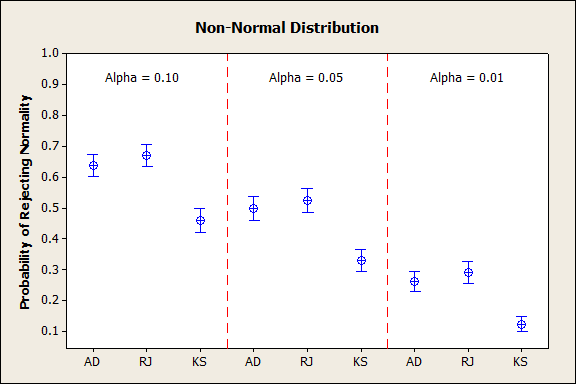
小結
總而言之,AD檢驗從來都不是最糟糕的檢驗,但在檢驗離群值方面,其效果不及RJ檢驗。如果您要分析制造過程中的數據往往會產生單個離群值,則最適合使用Ryan-Joiner檢驗。
RJ檢驗在情形1和情形3下均表現出色,但是當數據發生變化時(情形2),在檢驗非正態性方面表現不佳。如果您要分析制造過程中的數據,該數據由于意外更改而趨于變化,那么AD檢驗是最合適的。
KS檢驗在任何情況下均表現不佳。
在后續文章中,我還將討論當從正態分布模擬數據并且對數據進行一定程度的舍入時,這三個檢驗在不拒絕正態性方面的表現如何。
審核編輯:符乾江
-
Minitab
+關注
關注
0文章
177瀏覽量
11711 -
數據分析
+關注
關注
2文章
1452瀏覽量
34077
發布評論請先 登錄
相關推薦
RJ45網口PCB設計:制造與實踐要點
請問ADS1672用哪種雙端輸入雙端輸出的PGA匹配?
rj45-rj45六類跳線詳細介紹
正性光刻對掩膜版的要求
RJ45與光纖接口的轉接方法 RJ45接口的安全性問題分析
RJ45轉接頭的用途和分類 如何判斷RJ45線纜質量
RJ45網絡故障排除技巧 RJ45網線的長度對信號影響
RJ45連接速度與性能分析 RJ45插頭的類型及其應用
RJ45網絡接口的安裝指南 RJ45與其他網絡接口的區別
用MII to copper模式來進行MCU->DP83869HM->RJ45之間的通信,RJ45網絡連接不通的原因?
具有三態輸出的八進制正邊三柵D型觸發器SN74ALVCH374 數據表

RJ45連接器的優勢知多少?解讀LP系列RJ45連接器不止快更可靠

三態正邊沿觸發式高速CMOS邏輯八路 D型觸發器CDx4HC374數據表

什么是RJ45接口?RJ45接口有什么用?





 AD、RJ和KS-哪種正態性檢驗是最好的
AD、RJ和KS-哪種正態性檢驗是最好的










評論