Σ-Δ型ADC
Σ-Δ轉換器又稱為過采樣轉換器,其中Δ表示增量,∑表示積分或求和。與其他ADC不同的是,Σ-Δ型ADC不是直接對抽樣數據的數值做量化編碼,而是根據前后數值的差值(增量)做量化編碼。由于不是對大的絕對幅值做編碼,而是對增量編碼,因此使用低分辨率的一位量化器就能滿足要求。
組成:
Σ-Δ型ADC由兩部分組成:簡單的模擬電路(Σ-Δ調制器)和復雜的數字信號處理電路(數字濾波和采樣抽取器)。以一階Σ-Δ型ADC為例,它是由一個積分器,比較器,加法電路,時鐘和開關等組成的模擬電路和數字信號處理電路組成。可以說,Σ-Δ轉換器的數字特性多于模擬特性。示意圖如下:
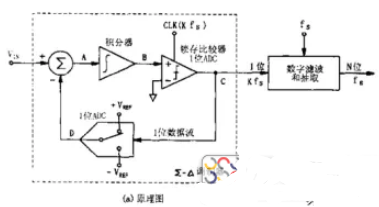
圖1 Σ-Δ轉換器原理圖
工作原理:
1》 Σ-Δ轉換器是利用低分辨率的ADC(通常為1位)以及高采樣速率(過采樣)對模擬信號抽樣并對增量進行量化,即得到數字Σ-Δ碼。
2》 送入數字抽取濾波器進行噪聲整形和數字濾波技術,提高數字信號分辨率。
3》 最后,通過采樣抽取過程降低輸出端的有效采樣速率,去除多余信息。
與其他ADC相比,Σ-Δ型ADC本質上是一種以高速抽樣率來換取高位量化,即以速率來換取分辨率的方案。
Σ-ΔADC的原理涉及到的三個概念:過采樣(over sampling),噪聲整形(noise shaping),數字濾波和采樣抽取。
過采樣:
根據奈奎斯特采樣定律,我們知道當采樣頻率≥2輸入信號頻率時,才能保留原始數據的信息。當采樣頻率kfs》》2時,被稱為過采樣。
從頻域上看,采樣實際上是采樣信號與輸入信號和量化噪聲做卷積,而采樣頻率越高,則頻帶越寬。因此當過采樣時候,實際上是把輸入信號和量化噪聲進行了展頻處理,而噪聲的總功率不變的情況下,頻譜擴展后,頻譜密度就降低了。我們看圖2,在奈奎斯特頻率下采樣,其中陰影部分為量化噪聲,這時候加一個低通濾波器,則可把部分噪聲濾除,但效果并不明顯。圖3則是過采樣后加低通,長方形的量化噪聲被展頻了,但是密度低了,經過了低通后,濾除的噪聲就會變多了。
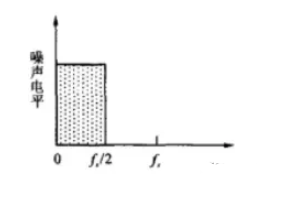
圖2 奈奎斯特頻率采樣

圖3 過采樣
同時,過采樣會降低后端模擬抗混疊濾波器的滾降要求。依據奈奎斯特準則,要求傳輸無失真,就要求滾降系數α越趨近于0越好,而越小則濾波器的設計難度越高。而過采樣則會在前期就讓數字濾波器將f/2到kf/2之間的量化噪聲消除(k為過采樣比),這樣就把總信噪比提高了10log10(k)數字濾波器將fS/2和k*fS/2之間的量化噪聲從輸出中消除,其結果是總信噪比提高了相當于10log10(k)。即大概信噪比提高6dB(1位),過采樣比高4倍,因此需要合理設計過采樣比。
噪聲整形:
噪聲整形技術通常是指用差分電路(Δ)和累加器(Σ)設計電路,使量化噪聲的頻譜密度從原先的均勻分布轉變成向高頻段分布,如圖3。經過整形后的噪聲功率不變,但低頻功率譜密度要比整形之前降很多。噪聲譜經過調制器的整形之后,數字濾波器就可以消除大部分量化噪聲能量,從而大幅提高總信噪比(以及相應的動態范圍)。

圖4 Σ-Δ調制后量化噪聲
數字濾波和采樣抽取:
這一部分是通過數字低通濾波器來完成的,經過Σ-Δ調制器后,噪聲在f/2以內的幾乎沒有,這時候通過數字濾波器,則量化噪聲中的高頻部分就被消除了,只剩下了少部分的低頻量化噪聲。由于之前的過采樣,使得頻率提高,所以濾波后對數據進行抽取,將高速率低精度的數字信號轉換成低速率高精度的數字信號輸出。
優點:精度高,線性度好,對輸入信號幅值變化不敏感,轉換速率高于積分型和壓頻變換型ADC;由于過采樣技術,抗干擾能力強。
缺點:高速Σ-Δ型ADC的價格相對較高;在轉換速率相同的條件下,比積分型和逐次逼近型ADC的功耗高
應用:
由于過采樣技術的應用,Σ-Δ型ADC對輸入頻率有要求,輸入信號頻率過高則會超過器件的極限頻率。也因此,Σ-Δ型ADC主要用于高分辨率的中、低頻測量和音頻電路。
溫度檢測電路,由于精度高、采樣率低的特點,Σ-Δ型ADC被廣泛應用。
而由于Σ-Δ型ADC的動態范圍較高,也廣泛應用于數字音頻電路中。
至此,ADC的四種經典類型原理及其應用已經介紹完畢,被人忽略的ADC系列也完結了。實際使用中還會碰到一些其他種類的,這里不再提及了。以后在實際工作中,碰到硬件調試的情況并不多見。但起碼應該做到,見到應用場景,能反應出來是哪種ADC,有哪些需要注意的點。
-
模擬電路
+關注
關注
125文章
1561瀏覽量
102803 -
adc
+關注
關注
98文章
6515瀏覽量
545107 -
低通濾波器
+關注
關注
14文章
476瀏覽量
47468 -
Σ-Δ
+關注
關注
0文章
5瀏覽量
3635
發布評論請先 登錄
相關推薦
Σ-Δ型ADC工作原理詳解
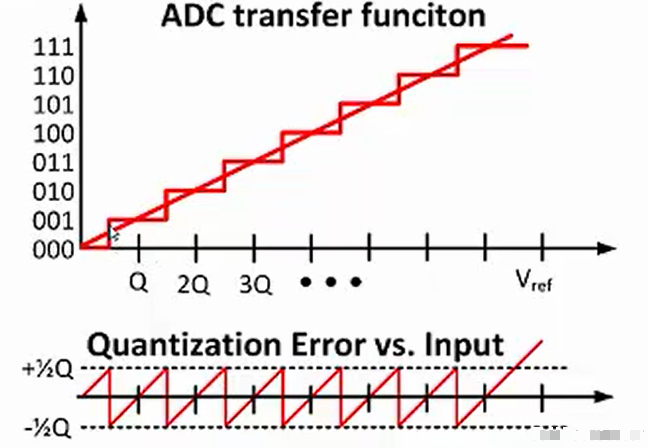
逐次逼近型A/D轉換器的基本原理
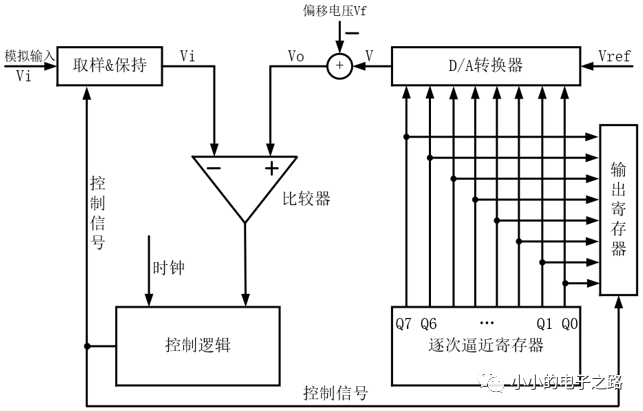
揭秘∑-Δ ADC的工作原理
Σ-Δ ADC的工作原理
ADC的工作原理與選型
基于RoboMasterC型開發板的ADC測量電壓實驗
逐次逼近型ADC的工作原理及優缺點
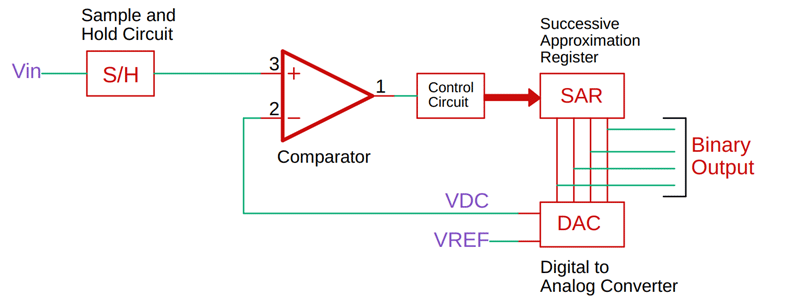
ADC的基本結構、分類及工作原理
ADC采樣保持電路的工作原理和技術指標
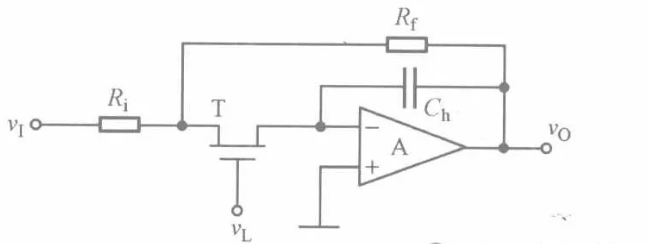




 Σ-Δ型ADC工作原理及應用
Σ-Δ型ADC工作原理及應用










評論