和求最大深度一個套路?
111.二叉樹的最小深度
題目地址:https://leetcode-cn.com/problems/minimum-depth-of-binary-tree/
給定一個二叉樹,找出其最小深度。
最小深度是從根節點到最近葉子節點的最短路徑上的節點數量。
說明:葉子節點是指沒有子節點的節點。
示例:
給定二叉樹[3,9,20,null,null,15,7],

返回它的最小深度 2.
思路
看完了這篇104.二叉樹的最大深度,再來看看如何求最小深度。
直覺上好像和求最大深度差不多,其實還是差不少的。
遍歷順序上依然是后序遍歷(因為要比較遞歸返回之后的結果),但在處理中間節點的邏輯上,最大深度很容易理解,最小深度可有一個誤區,如圖:
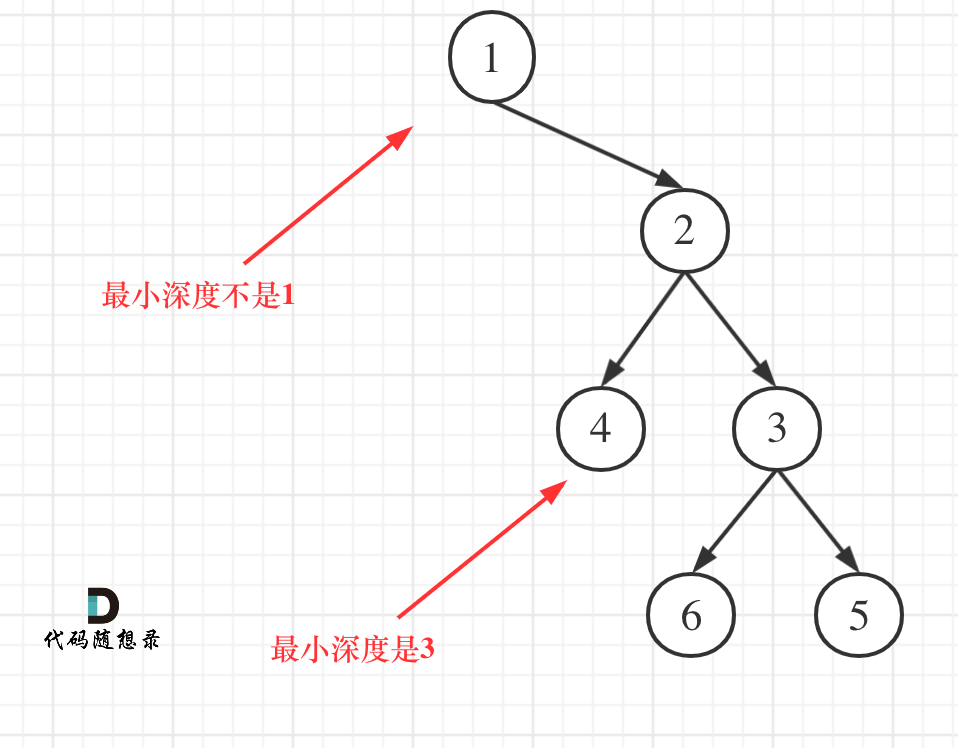
這就重新審題了,題目中說的是:最小深度是從根節點到最近葉子節點的最短路徑上的節點數量。,注意是葉子節點。
什么是葉子節點,左右孩子都為空的節點才是葉子節點!
遞歸法
來來來,一起遞歸三部曲:
- 確定遞歸函數的參數和返回值
參數為要傳入的二叉樹根節點,返回的是int類型的深度。
代碼如下:
intgetDepth(TreeNode*node)
- 確定終止條件
終止條件也是遇到空節點返回0,表示當前節點的高度為0。
代碼如下:
if(node==NULL)return0;
- 確定單層遞歸的邏輯
這塊和求最大深度可就不一樣了,一些同學可能會寫如下代碼:
intleftDepth=getDepth(node->left);
intrightDepth=getDepth(node->right);
intresult=1+min(leftDepth,rightDepth);
returnresult;
這個代碼就犯了此圖中的誤區:

如果這么求的話,沒有左孩子的分支會算為最短深度。
所以,如果左子樹為空,右子樹不為空,說明最小深度是 1 + 右子樹的深度。
反之,右子樹為空,左子樹不為空,最小深度是 1 + 左子樹的深度。最后如果左右子樹都不為空,返回左右子樹深度最小值 + 1 。
代碼如下:
intleftDepth=getDepth(node->left);//左
intrightDepth=getDepth(node->right);//右
//中
//當一個左子樹為空,右不為空,這時并不是最低點
if(node->left==NULL&&node->right!=NULL){
return1+rightDepth;
}
//當一個右子樹為空,左不為空,這時并不是最低點
if(node->left!=NULL&&node->right==NULL){
return1+leftDepth;
}
intresult=1+min(leftDepth,rightDepth);
returnresult;
遍歷的順序為后序(左右中),可以看出:求二叉樹的最小深度和求二叉樹的最大深度的差別主要在于處理左右孩子不為空的邏輯。
整體遞歸代碼如下:
classSolution{
public:
intgetDepth(TreeNode*node){
if(node==NULL)return0;
intleftDepth=getDepth(node->left);//左
intrightDepth=getDepth(node->right);//右
//中
//當一個左子樹為空,右不為空,這時并不是最低點
if(node->left==NULL&&node->right!=NULL){
return1+rightDepth;
}
//當一個右子樹為空,左不為空,這時并不是最低點
if(node->left!=NULL&&node->right==NULL){
return1+leftDepth;
}
intresult=1+min(leftDepth,rightDepth);
returnresult;
}
intminDepth(TreeNode*root){
returngetDepth(root);
}
};
精簡之后代碼如下:
classSolution{
public:
intminDepth(TreeNode*root){
if(root==NULL)return0;
if(root->left==NULL&&root->right!=NULL){
return1+minDepth(root->right);
}
if(root->left!=NULL&&root->right==NULL){
return1+minDepth(root->left);
}
return1+min(minDepth(root->left),minDepth(root->right));
}
};
精簡之后的代碼根本看不出是哪種遍歷方式,所以依然還要強調一波:如果對二叉樹的操作還不熟練,盡量不要直接照著精簡代碼來學。
迭代法
相對于104.二叉樹的最大深度,本題還可以使用層序遍歷的方式來解決,思路是一樣的。
如果對層序遍歷還不清楚的話,可以看這篇:二叉樹:層序遍歷登場!
需要注意的是,只有當左右孩子都為空的時候,才說明遍歷的最低點了。如果其中一個孩子為空則不是最低點
代碼如下:(詳細注釋)
classSolution{
public:
intminDepth(TreeNode*root){
if(root==NULL)return0;
intdepth=0;
queueque;
que.push(root);
while(!que.empty()){
intsize=que.size();
depth++;//記錄最小深度
for(inti=0;iif(node->left)que.push(node->left);
if(node->right)que.push(node->right);
if(!node->left&&!node->right){//當左右孩子都為空的時候,說明是最低點的一層了,退出
returndepth;
}
}
}
returndepth;
}
};
其他語言版本
Java
classSolution{
/**
*遞歸法,相比求MaxDepth要復雜點
*因為最小深度是從根節點到最近**葉子節點**的最短路徑上的節點數量
*/
publicintminDepth(TreeNoderoot){
if(root==null){
return0;
}
intleftDepth=minDepth(root.left);
intrightDepth=minDepth(root.right);
if(root.left==null){
returnrightDepth+1;
}
if(root.right==null){
returnleftDepth+1;
}
//左右結點都不為null
returnMath.min(leftDepth,rightDepth)+1;
}
}
classSolution{
/**
*迭代法,層序遍歷
*/
publicintminDepth(TreeNoderoot){
if(root==null){
return0;
}
Dequedeque=newLinkedList<>();
deque.offer(root);
intdepth=0;
while(!deque.isEmpty()){
intsize=deque.size();
depth++;
for(inti=0;iif(poll.left==null&&poll.right==null){
//是葉子結點,直接返回depth,因為從上往下遍歷,所以該值就是最小值
returndepth;
}
if(poll.left!=null){
deque.offer(poll.left);
}
if(poll.right!=null){
deque.offer(poll.right);
}
}
}
returndepth;
}
}
Python
遞歸法:
classSolution:
defminDepth(self,root:TreeNode)->int:
ifnotroot:
return0
ifnotroot.leftandnotroot.right:
return1
min_depth=10**9
ifroot.left:
min_depth=min(self.minDepth(root.left),min_depth)#獲得左子樹的最小高度
ifroot.right:
min_depth=min(self.minDepth(root.right),min_depth)#獲得右子樹的最小高度
returnmin_depth+1
迭代法:
classSolution:
defminDepth(self,root:TreeNode)->int:
ifnotroot:
return0
que=deque()
que.append(root)
res=1
whileque:
for_inrange(len(que)):
node=que.popleft()
#當左右孩子都為空的時候,說明是最低點的一層了,退出
ifnotnode.leftandnotnode.right:
returnres
ifnode.leftisnotNone:
que.append(node.left)
ifnode.rightisnotNone:
que.append(node.right)
res+=1
returnres
--- EOF ---審核編輯 :李倩
-
節點
+關注
關注
0文章
220瀏覽量
24454 -
函數
+關注
關注
3文章
4338瀏覽量
62749 -
二叉樹
+關注
關注
0文章
74瀏覽量
12349
原文標題:二叉樹的最小深度!
文章出處:【微信號:TheAlgorithm,微信公眾號:算法與數據結構】歡迎添加關注!文章轉載請注明出處。
發布評論請先 登錄
相關推薦
嵌入式學習-飛凌嵌入式ElfBoard ELF 1板卡-初識設備樹之設備樹組成和結構
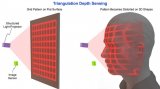
3D深度感測的原理和使用二極管激光來實現深度感測的優勢
飛凌嵌入式ElfBoard ELF 1板卡-初識設備樹之設備樹組成和結構
MCU最小系統電路設計指南

GPU深度學習應用案例
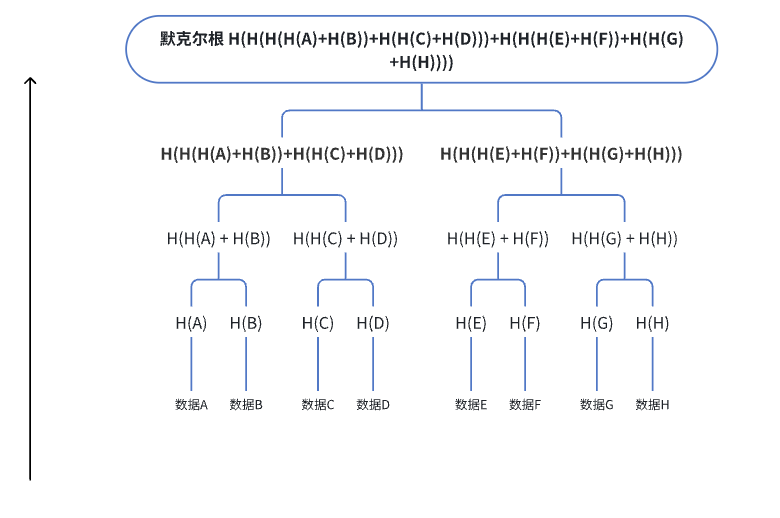
什么是默克爾樹(Merkle Tree)?如何計算默克爾根?
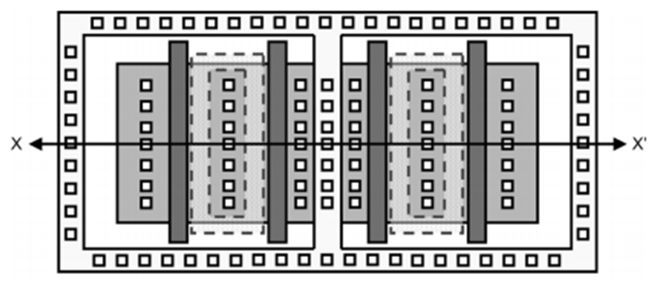
多叉指MOSFET器件靜電防護魯棒性提升技巧
示波器怎么設置存儲深度?
原理圖設計里兩顆重要的樹(國產EDA)
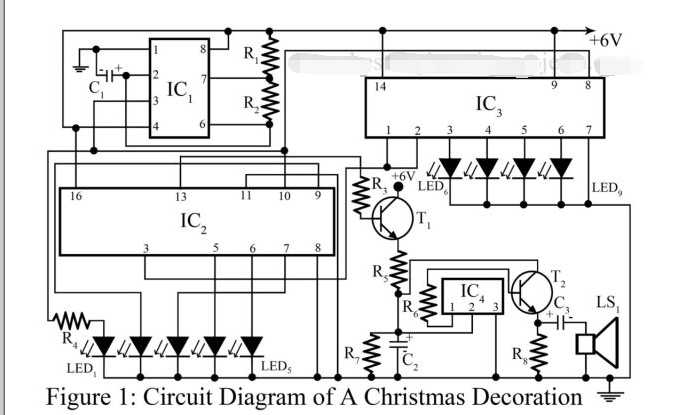
圣誕樹燈電路圖分享




 二叉樹的最小深度
二叉樹的最小深度











評論