負反饋因其可以穩定增益、減小失真、擴展帶寬、變換阻抗等功能而在電子、控制等諸多領域發揮著重大作用。小至一顆電源芯片,大至一輛汽車,都在負反饋技術的幫助下使我們的生活變得更豐富。然而,負反饋的使用也是有代價的,即可能會導致系統不穩定。
為了了解系統的穩定性情況,最直接、精確的方式就是測量系統的相位裕量(Phase Margin/ PM),我們通常會使用環路分析儀進行測試。
小編今天向大家介紹另一種方法,即通過測量過沖情況(OS)得到系統的相位裕量。
電路的二階系統化
一些常見的反饋電路,通常都是二階系統,我們以運放容性帶載為例來討論:
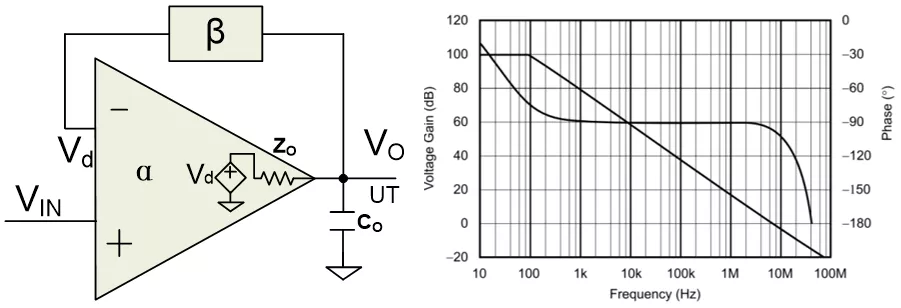
*運放的容性負載 *典型通用運放的開環增益曲線
一個典型通用運放的開環增益曲線如上圖所示。它一般擁有一個低頻的主極點,如100Hz,高頻極點通常會被設計為遠高于穿越頻率,所以常規的運放電路是穩定的。
當運放存在容性負載的時候,開環輸出電抗(Zo)與輸出電容(Co)形成的極點會處在反饋環路內,當極點頻率靠近或小于穿越頻率,則會使得系統的相位裕度明顯降低,導致不穩定的情況發生。
所以,一個運放帶容性負載的放大電路,其傳遞函數可以表示為:
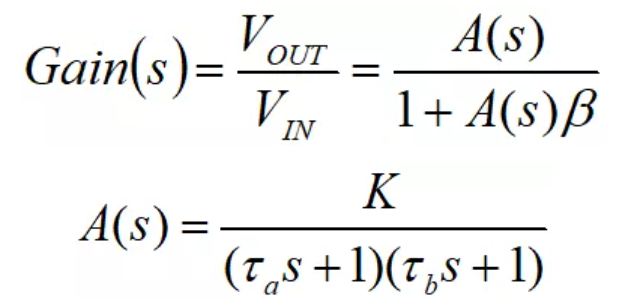
其中,K為運放的DC開環增益,β是反饋系數(作為跟隨器時,β=1,100倍放大時,β=0.01)。
1/τa是運放的低頻主極點的角頻率,1/τb是Zo和Co產生寄生極點的角頻率。可見,τa》》 τb。
上式可被轉換為標準的二階系統
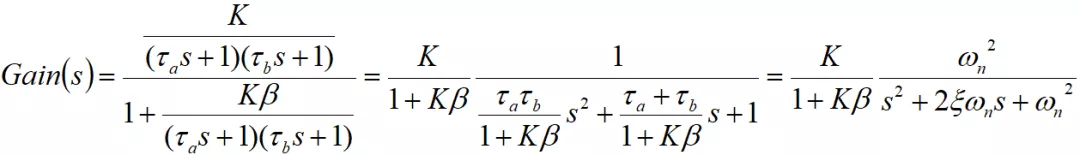
由于K為運放的DC開環增益,所以Kβ》》1
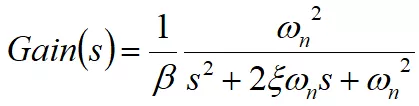
其中,ωn為電路的自然頻率,ξ為阻尼系數,且
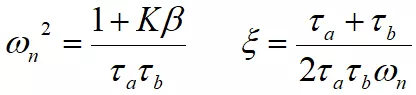
時域過沖與阻尼系數的關系
我們知道,系統處于欠阻尼狀態,即0《ξ《1,才會存在過沖的情況。
對一個標準的二階系統來說,
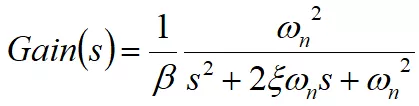
可以求得其單位階躍響應函數為:
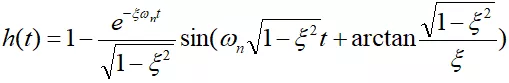
求得階躍響應第一個峰值對應的時間為:
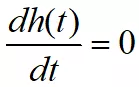
所以過沖為
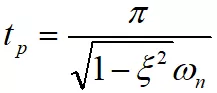
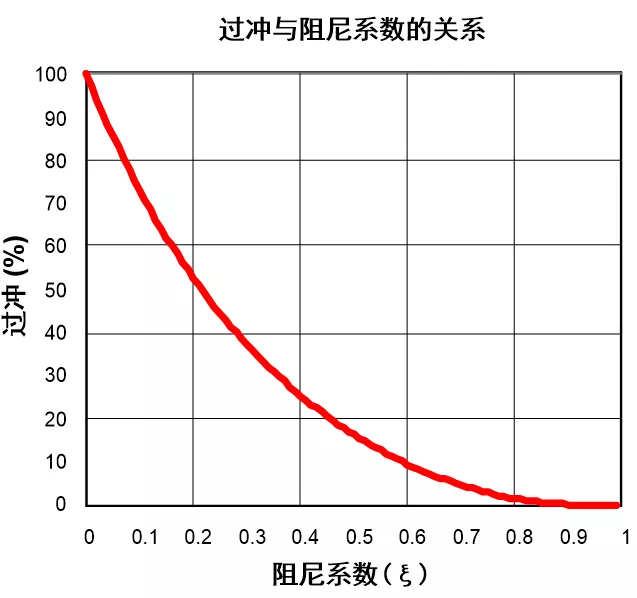
因此我們可以繪制如下過沖與阻尼系數的曲線
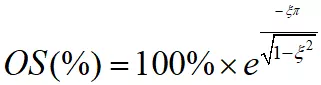
*過沖與阻尼系數的關系
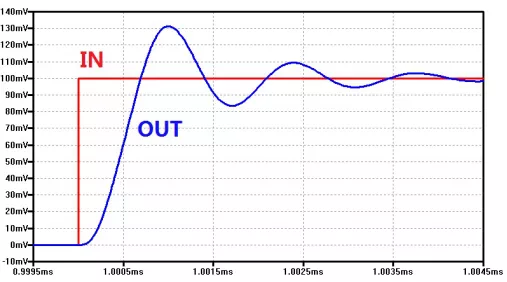
過沖可以經由在輸入端給予一個小的階躍信號,并測量輸出端得到。如下圖是在ξ=0.35的系統中在1ms時使用100mV階躍輸入所測得的過沖情況,過沖為31%。
相位裕量與阻尼系數的關系
我們接下去分析阻尼系數與相位裕量(Phase Margin)的關系
系統的環路增益為:
為了求得系統穿越頻率ωc ,可令|A(s)β|=1
求得
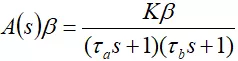
所以相位裕度
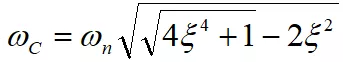
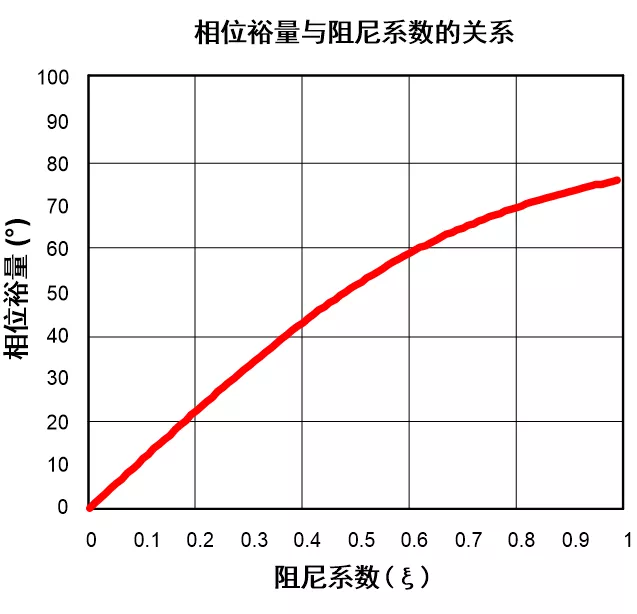
具此我們可以繪制如下相位裕量與阻尼系數的曲線
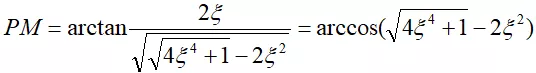
*相位裕量與阻尼系數的關系
相位裕量與過沖的關系
由此,我們借由阻尼系數,得到相位裕量與過沖的關系,繪制曲線如下
*相位裕量與過沖的關系
由上圖可知,當相位裕量大于70?以上時已經幾乎沒有過沖
相位裕量60? 時, OS(60?)≈8.8%
相位裕量45? 時, OS(45?) ≈23.4%
我們的討論是基于二階系統的,所以如果實際的電路并非二階系統,那么相位裕量與過沖的關系將并不嚴格遵循上述推論。但幸運的是,現實中的大部分電路都近似于二階系統,所以通過觀察過沖情況(OS)來判斷系統穩定性的方法,對于有時候的系統調試(特別是,對于差分放大器或者SOC等并沒有提供反饋引腳而無法采用環路分析儀的場合),或者定性分析,都是大有裨益的。
免責聲明:本文為網絡轉載文章,轉載此文目的在于傳播相關技術知識,版權歸原作者所有,如涉及侵權,請聯系小編刪除。
編輯:jq
-
差分放大器
+關注
關注
8文章
496瀏覽量
52602 -
soc
+關注
關注
38文章
4274瀏覽量
220611 -
函數
+關注
關注
3文章
4359瀏覽量
63524
原文標題:過沖與相位裕量
文章出處:【微信號:村田中文技術社區,微信公眾號:村田中文技術社區】歡迎添加關注!文章轉載請注明出處。
發布評論請先 登錄
相關推薦
使用DAC61416輸出方波電壓時,輸出存在很大的過沖如何解決?
lmx2531lq1910e的環路濾波器推薦的相位裕度為什么設計在70度?
用運放OPA2846做脈沖小信號放大電路,信號會有一個過沖,怎么產生的?
使用TINA進行穩定性分析時用幾種不同方式出現了較大的相位裕度差異,為什么?
如何判斷電壓-電流轉換電路的環路穩定性?
OPA189 phase margin相位裕度是AOL*β在0dB時的相位即80°,為什么不是180-80=100°呢?
LMH5401輸出飽和時負過沖怎么解決?
AD7741輸出頻率過沖是什么原因導致的?
MAX13487 RS485總線AB電壓差有很大的過沖是怎么回事?
環路濾波器的環路帶寬及相位裕度簡析



















評論