簡介
支持向量機基本上是最好的有監督學習算法了。最開始接觸SVM是去年暑假的時候,老師要求交《統計學習理論》的報告,那時去網上下了一份入門教程,里面講的很通俗,當時只是大致了解了一些相關概念。
這次斯坦福提供的學習材料,讓我重新學習了一些SVM知識。我看很多正統的講法都是從VC 維理論和結構風險最小原理出發,然后引出SVM什么的,還有些資料上來就講分類超平面什么的。
這份材料從前幾節講的logistic回歸出發,引出了SVM,既揭示了模型間的聯系,也讓人覺得過渡更自然。
重新審視logistic回歸
Logistic回歸目的是從特征學習出一個0/1分類模型,而這個模型是將特性的線性組合作為自變量,由于自變量的取值范圍是負無窮到正無窮。
因此,使用logistic函數(或稱作sigmoid函數)將自變量映射到(0,1)上,映射后的值被認為是屬于y=1的概率。
形式化表示就是
假設函數
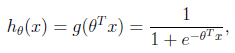
其中x是n維特征向量,函數g就是logistic函數。
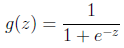 的圖像是
的圖像是
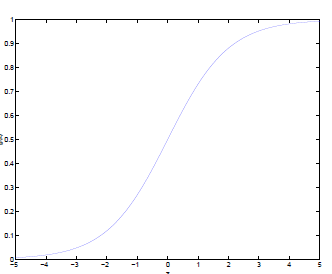
可以看到,將無窮映射到了(0,1)。
而假設函數就是特征屬于y=1的概率。
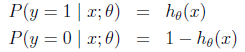
當我們要判別一個新來的特征屬于哪個類時,只需求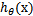 ,若大于0.5就是y=1的類,反之屬于y=0類。
,若大于0.5就是y=1的類,反之屬于y=0類。
再審視一下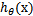 ,發現
,發現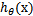 只和
只和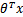 有關,
有關,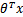 >0,那么
>0,那么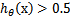 ,g(z)只不過是用來映射,真實的類別決定權還在
,g(z)只不過是用來映射,真實的類別決定權還在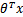 。還有當
。還有當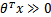 時,
時,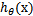 =1,反之
=1,反之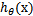 =0。
=0。
如果我們只從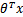 出發,希望模型達到的目標無非就是讓訓練數據中y=1的特征
出發,希望模型達到的目標無非就是讓訓練數據中y=1的特征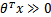 ,而是y=0的特征
,而是y=0的特征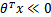 。
。
Logistic回歸就是要學習得到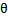 ,使得正例的特征遠大于0,負例的特征遠小于0,強調在全部訓練實例上達到這個目標。
,使得正例的特征遠大于0,負例的特征遠小于0,強調在全部訓練實例上達到這個目標。
圖形化表示如下:
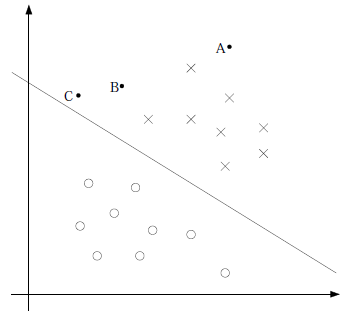
中間那條線是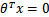 ,logistic回顧強調所有點盡可能地遠離中間那條線。學習出的結果也就中間那條線。
,logistic回顧強調所有點盡可能地遠離中間那條線。學習出的結果也就中間那條線。
考慮上面3個點A、B和C。從圖中我們可以確定A是×類別的,然而C我們是不太確定的,B還算能夠確定。這樣我們可以得出結論,我們更應該關心靠近中間分割線的點,讓他們盡可能地遠離中間線,而不是在所有點上達到最優。
因為那樣的話,要使得一部分點靠近中間線來換取另外一部分點更加遠離中間線。我想這就是支持向量機的思路和logistic回歸的不同點,一個考慮局部(不關心已經確定遠離的點),一個考慮全局(已經遠離的點可能通過調整中間線使其能夠更加遠離)。這是我的個人直觀理解。
形式化表示
我們這次使用的結果標簽是y=-1,y=1,替換在logistic回歸中使用的y=0和y=1。同時將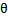 替換成w和b。
替換成w和b。
以前的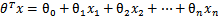 ,其中認為
,其中認為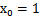 。現在我們替換
。現在我們替換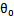 為b,后面替換
為b,后面替換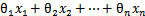 為
為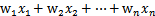 (即
(即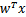 )。這樣,我們讓
)。這樣,我們讓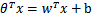 ,進一步
,進一步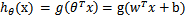 。
。
也就是說除了y由y=0變為y=-1,只是標記不同外,與logistic回歸的形式化表示沒區別。再明確下假設函數
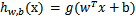
上一節提到過我們只需考慮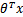 的正負問題,而不用關心g(z),因此我們這里將g(z)做一個簡化,將其簡單映射到y=-1和y=1上。映射關系如下:
的正負問題,而不用關心g(z),因此我們這里將g(z)做一個簡化,將其簡單映射到y=-1和y=1上。映射關系如下:
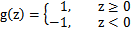
函數間隔(functional margin)和幾何間隔(geometric margin)
給定一個訓練樣本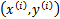 ,x是特征,y是結果標簽。i表示第i個樣本。我們定義函數間隔如下:
,x是特征,y是結果標簽。i表示第i個樣本。我們定義函數間隔如下:
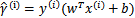
可想而知,當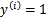 時,在我們的g(z)定義中,
時,在我們的g(z)定義中,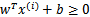 ,
,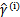 的值實際上就是
的值實際上就是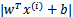 。反之亦然。
。反之亦然。
為了使函數間隔最大(更大的信心確定該例是正例還是反例),當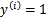 時,
時,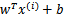 應該是個大正數,反之是個大負數。因此函數間隔代表了我們認為特征是正例還是反例的確信度。
應該是個大正數,反之是個大負數。因此函數間隔代表了我們認為特征是正例還是反例的確信度。
繼續考慮w和b,如果同時加大w和b,比如在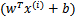 前面乘個系數比如2,那么所有點的函數間隔都會增大二倍,這個對求解問題來說不應該有影響,因為我們要求解的是
前面乘個系數比如2,那么所有點的函數間隔都會增大二倍,這個對求解問題來說不應該有影響,因為我們要求解的是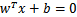 ,同時擴大w和b對結果是無影響的。
,同時擴大w和b對結果是無影響的。
這樣,我們為了限制w和b,可能需要加入歸一化條件,畢竟求解的目標是確定唯一一個w和b,而不是多組線性相關的向量。這個歸一化一會再考慮。
剛剛我們定義的函數間隔是針對某一個樣本的,現在我們定義全局樣本上的函數間隔
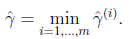
說白了就是在訓練樣本上分類正例和負例確信度最小那個函數間隔。
接下來定義幾何間隔
假設我們有了B點所在的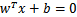 分割面。任何其他一點,比如A到該面的距離以
分割面。任何其他一點,比如A到該面的距離以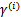 表示,假設B就是A在分割面上的投影。
表示,假設B就是A在分割面上的投影。
我們知道向量BA的方向是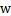 (分割面的梯度),單位向量是
(分割面的梯度),單位向量是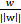 。A點是
。A點是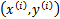 ,所以B點是x=
,所以B點是x=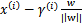 (利用初中的幾何知識),帶入
(利用初中的幾何知識),帶入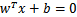 得,
得,
進一步得到
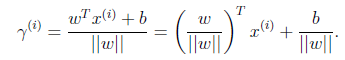
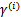 實際上就是點到平面距離。
實際上就是點到平面距離。
再換種更加優雅的寫法:
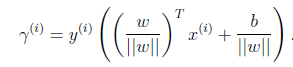
當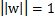 時,不就是函數間隔嗎?是的,前面提到的函數間隔歸一化結果就是幾何間隔。
時,不就是函數間隔嗎?是的,前面提到的函數間隔歸一化結果就是幾何間隔。
他們為什么會一樣呢?因為函數間隔是我們定義的,在定義的時候就有幾何間隔的色彩。同樣,同時擴大w和b,w擴大幾倍,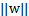 就擴大幾倍,結果無影響。同樣定義全局的幾何間隔
就擴大幾倍,結果無影響。同樣定義全局的幾何間隔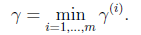
最優間隔分類器(optimal margin classifier)
回想前面我們提到我們的目標是尋找一個超平面,使得離超平面比較近的點能有更大的間距。也就是我們不考慮所有的點都必須遠離超平面,我們關心求得的超平面能夠讓所有點中離它最近的點具有最大間距。
形象的說,我們將上面的圖看作是一張紙,我們要找一條折線,按照這條折線折疊后,離折線最近的點的間距比其他折線都要大。形式化表示為:
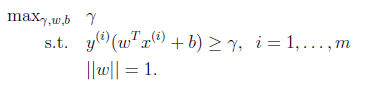
這里用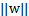 =1規約w,使得
=1規約w,使得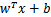 是幾何間隔。
是幾何間隔。
到此,我們已經將模型定義出來了。如果求得了w和b,那么來一個特征x,我們就能夠分類了,稱為最優間隔分類器。接下的問題就是如何求解w和b的問題了。
由于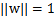 不是凸函數,我們想先處理轉化一下,考慮幾何間隔和函數間隔的關系,
不是凸函數,我們想先處理轉化一下,考慮幾何間隔和函數間隔的關系,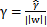 ,我們改寫一下上面的式子:
,我們改寫一下上面的式子:
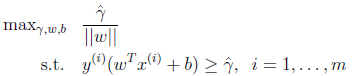
這時候其實我們求的最大值仍然是幾何間隔,只不過此時的w不受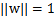 的約束了。然而這個時候目標函數仍然不是凸函數,沒法直接代入優化軟件里計算。我們還要改寫。
的約束了。然而這個時候目標函數仍然不是凸函數,沒法直接代入優化軟件里計算。我們還要改寫。
前面說到同時擴大w和b對結果沒有影響,但我們最后要求的仍然是w和b的確定值,不是他們的一組倍數值,因此,我們需要對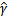 做一些限制,以保證我們解是唯一的。
做一些限制,以保證我們解是唯一的。
這里為了簡便我們取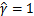 。這樣的意義是將全局的函數間隔定義為1,也即是將離超平面最近的點的距離定義為
。這樣的意義是將全局的函數間隔定義為1,也即是將離超平面最近的點的距離定義為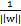 。由于求
。由于求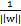 的最大值相當于求
的最大值相當于求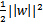 的最小值,因此改寫后結果為:
的最小值,因此改寫后結果為:
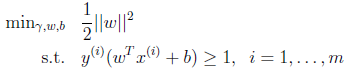
這下好了,只有線性約束了,而且是個典型的二次規劃問題(目標函數是自變量的二次函數)。代入優化軟件可解。
到這里發現,這個講義雖然沒有像其他講義一樣先畫好圖,畫好分類超平面,在圖上標示出間隔那么直觀,但每一步推導有理有據,依靠思路的流暢性來推導出目標函數和約束。
—版權聲明—
僅用于學術分享,版權屬于原作者。
若有侵權,請聯系 刪除或修改!
轉自:JerryLead
http://www.cnblogs.com/jerrylead/archive/2011/03/13/1982639.html
編輯:jq
-
算法
+關注
關注
23文章
4622瀏覽量
93063 -
向量機
+關注
關注
0文章
166瀏覽量
20888 -
SVM
+關注
關注
0文章
154瀏覽量
32503
原文標題:優雅的讀懂支持向量機 SVM 算法
文章出處:【微信號:gh_f39db674fbfd,微信公眾號:尖刀視】歡迎添加關注!文章轉載請注明出處。
發布評論請先 登錄
相關推薦
計算機視覺技術的AI算法模型
機器學習算法原理詳解
一文帶你讀懂什么是工控機

如何利用一些小技巧實現SVM的增量式訓練




 一文帶你快速讀懂支持向量機 SVM 算法
一文帶你快速讀懂支持向量機 SVM 算法













評論