在知乎上看到一個比較有意思的話題,卷積為什么叫”卷“積?哈哈哈哈哈
其中有個動圖用卷毛巾生動形象的比喻了卷積的過程。
帶著好奇心先看一下我們最熟悉的卷積公式:
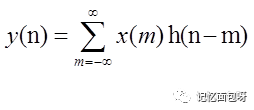
還可以改寫成:
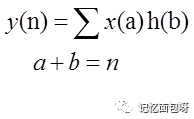
其中a,b表示a+b=n這條直線上所有的點。y(n)就表示這條直線上所有點對應的函數值x(a)h(b)的累加。
以下圖卷毛巾為例,將毛巾沿紅色虛線方向卷起來,設這條紅色虛線為a+b=5,卷起來后這條紅線上的所有函數值都累加到n=5這一點上,即是y(5)的值。
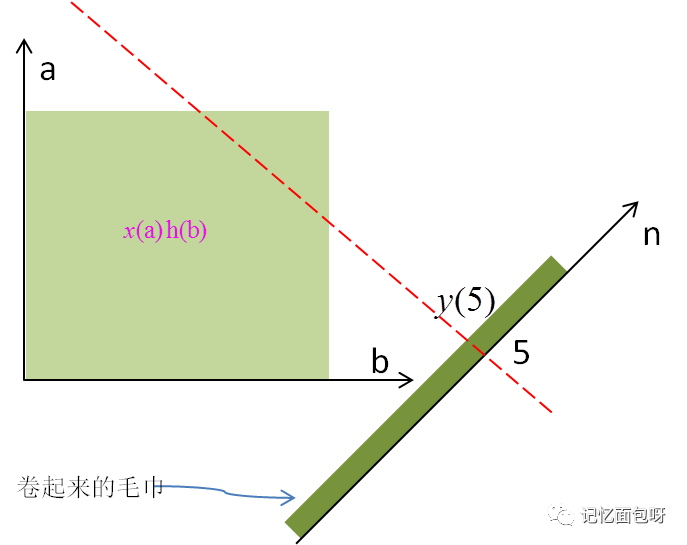
1.一維信號的卷積
上面只是從數學公式解釋了卷積是如何計算的,但卷積物理意義是什么呢?
學習信號與系統的時候總是聽老師說信號經過一個系統就是與這個系統進行卷積。所以我們先從一維信號來解釋一下。
(1)表示信號δ(t)經過某系統產生了輸出h(t)。
(2)將信號δ(t)延時τ后,輸出也延時了τ,為h(t-τ)。
(3)將1,2中信號疊加輸入系統后,產生輸出y(t)也進行了一個疊加,輸出等于h(t)+h(t-τ)。
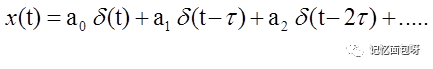
再假如有這樣一個x(t),由很多個δ(t)組成,這個δ(t)不正是沖激函數嘛。它經過系統會輸出什么?

由δ(t)沖激函數的性質
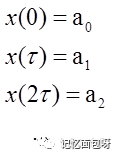
帶入便得到了卷積公式。
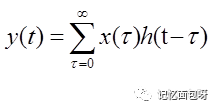
所以卷積的意義就是累加唄,得到的結果y(t)就表示在t這點的沖激響應和t之前所有沖激響應的”余波“的累加值。(這里累加下限τ=0是因為假設t《0時沒有信號的,不會對t這點產生影響)
2.二維圖像卷積
上升到二維空間,卷積公式變為
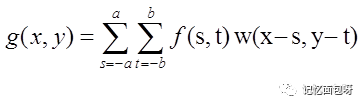
以高斯濾波為例,w(x,y)是二維高斯函數。
圖像f與w卷積,可以同樣理解為圖像經過系統w所產生的輸出,而圖像中每個像素點可以理解為一維卷積中的信號δ(t),最終的輸出也是每個像素點沖激響應累加的結果。
累加的上下標a,b代表著能對中心像素產生影響的周圍像素的范圍,而影響的大小取決于①它對中心像素的“余波”;②周圍像素點本身的像素值(相當于一維中的a0,a1 ,a2 。 。 。 。)。
舉個例子,當a,b都為2時,表示以某像素為中心3×3的矩陣內,所有像素都對此像素有影響。
想象一下這個3×3的矩陣中每個像素上都對高斯濾波器產生了沖激響應,可以想象成每個像素上有座山,山坡會延伸到周圍像素上,山的高度可以疊加,那中心點像素的山就是最高的了。
那中間山的高度是多少呢? 取決于:
①周圍像素對中心像素的“余波”;
f(x-1,y-1)在中心像素的“余波”為1,f(x-1,y)在中心像素的“余波”為2,f(x-1,y+1)在中心像素的“余波”為1,f(x,y-1)在中心像素的“余波”為2,f(x,y)自己貢獻了4,f(x,y+1)在中心像素的“余波”為2,f(x+1,y-1)在中心像素的“余波”為1,f(x+1,y)在中心像素的“余波”為2,f(x+1,y+1) 在中心像素的“余波”為1。
②周圍像素點本身的像素值
最終山的高度等于∑(某點像素值 × 其對中心點”余波“)。而“余波”不就是所用的模板嗎。
還有一點需要注意,這個模板并不是我們的w,而是將w翻轉了180度,方便與相同位置像素對應。
由卷積公式得下式,對應圖中相同顏色的相乘。
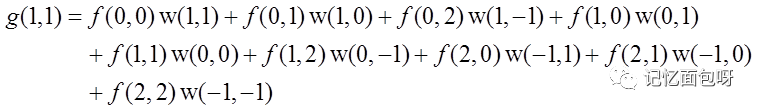
3.FPGA實現
理解了高斯濾波模板的意義,接下來就考慮如何用FPGA來實現了。由于圖像是一個像素一個像素流入FPGA的,所以怎樣將一個個像素流變成3×3的方塊與我們的模板相乘是一個問題。
還好altera ip核中有個shift_ram,可以將數據緩存后分行輸出。下圖就比較直觀的展現了它的功能。
所以我們需要將數據緩存兩行,每行640個像素,加上當前流入的像素,就可以構成需要的3×3的矩陣了。

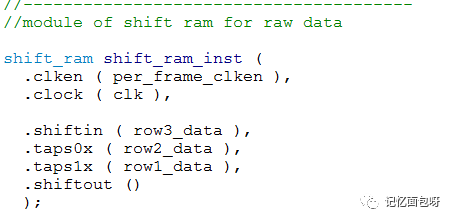
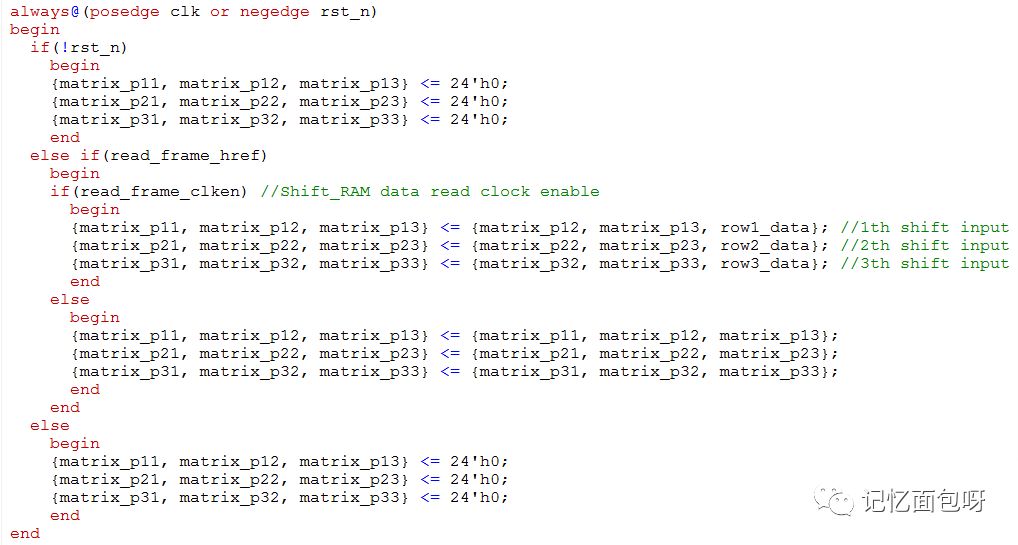
最后行場同步需要打兩拍是由于輸入數據的時候數據打了一拍,上圖構建矩陣時打了一拍,詳見完整代碼。
仿真結果
可以看出shift_ram在緩存兩行數據后,就可以三行數據同時輸出。就可以構成3×3的矩陣了。
接下來對這個3×3矩陣進行乘上對應系數再累加,便得到濾波后的像素啦。
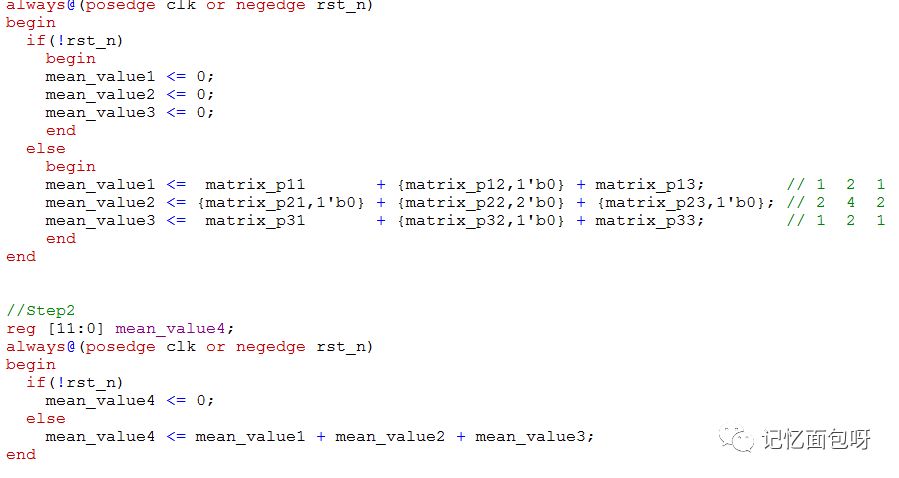
編輯:jq
-
FPGA
+關注
關注
1638文章
21861瀏覽量
610072 -
濾波
+關注
關注
10文章
672瀏覽量
56969 -
數據
+關注
關注
8文章
7230瀏覽量
90463 -
代碼
+關注
關注
30文章
4866瀏覽量
69788
原文標題:基于FPGA的圖像高斯濾波
文章出處:【微信號:zhuyandz,微信公眾號:FPGA之家】歡迎添加關注!文章轉載請注明出處。
發布評論請先 登錄
相關推薦
基于FPGA實現圖像直方圖設計
FPGA 實時信號處理應用 FPGA在圖像處理中的優勢
FPGA在圖像處理領域的優勢有哪些?
高斯卷積核函數在圖像采樣中的意義
高斯濾波的基本原理有哪些
基于FPGA的實時邊緣檢測系統設計,Sobel圖像邊緣檢測,FPGA圖像處理
FPGA設計中 Verilog HDL實現基本的圖像濾波處理仿真
什么是高斯光束




















評論