作者:劉安海,于惠鈞,黃星,龔星宇
0 引言
隨著我國工業化水平不斷地提高,地鐵車輛已經成為代步的主要交通工具,應用到各個城市中。電機作為地鐵車輛驅動系統的重要部分,其控制技術決定了地鐵運行性能的重要指標,該技術也成為研究的熱點。現在采用永磁同步電機(PMSM) 為地鐵車輛的驅動電機方法普遍存在。PMSM 結構緊湊、載重量大、故障維護方便等多種優勢,被廣泛應用于各種電器產品,城軌車輛等領域。國內對永磁同步電機調速系統的研究有很多, 大多數永磁同步電機調速系統仍然使用算法簡單、易于實現的PI 控制, 但這種控制方式局限性很大,參數不能隨時調整,系統控制精確度不高,應用范圍局限很大。PMSM 的控制采用PI 控制,但PI 參數很難得到精確值,不精確的比例積分參數可能會導致系統不穩定和無法控制。由于電機控制的變量參數多,耦合性強,因此必須微調其PI 參數以保持穩定和精確的工作,但PI 控制器無法自動調整其參數,可以引入遺傳算法,模糊控制算法,粒子群優化算法等來解決這些問題,這些算法不需要十分精確的數學模型,可用于解決復雜的非線性問題。電機的控制性能直接影響地鐵的整體性能,因此永磁同步電機的控制技術已成為研究熱點。文獻基于前饋補償的模糊PI 永磁同步電機調速系統,但是該算法局部搜索能力普遍較差;文獻采用矢量控制結合滑模控制建立了永磁同步電機調速系統模型,使系統控制良好,電機轉速超調量低,但沒有討論帶載下的轉速等情況。
PSO 優化算法編程簡單、收斂快等優點,采用該控制技術對PMSM 進行動態控制可以彌補傳統PI 控制的缺陷。
本文在電機PI 控制的基礎上將粒子群算法應用到“轉速- 電流”雙閉環PI 參數優化中,能快速逼近最優參數,實現地鐵車輛永磁同步電機運行跟平穩,系統精確性跟好。
1 PWSM在d-q坐標系下的數學模型
1.1 坐標變換
為了使PMSM 擁有直流電機的性能,利用坐標變換簡化數學模型。

式中:θ 是轉子位置角。
1.2 永磁同步電機的數學模型
對PMSM 的數學模型進行推導過程中,其數學模型建立假設前提有:
1) 永磁體材料的電導率為0;
2) 忽略齒槽和電樞反應影響;
3) 轉子上沒有阻尼繞組;
4) 定子各繞組互差120° ;
5) 各相繞組是正弦波形;
6) 各繞組的電感和電阻為定值。
上述前提推導下,數學模型電壓、磁鏈和轉矩方程為
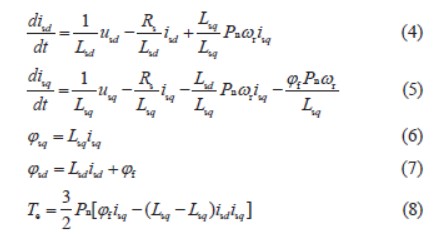
式中: usd 、usq 、isd 、isq 是dq 軸定子電壓和定子電流; ?sd 、?sq 、Lsd 、Lsq 是dq 軸定子磁鏈和定子電感;Rs 是電樞電阻; ?f 是永磁體磁鏈; Te 是電磁轉矩; ωr是轉子的機械角速度; Pn是極對數。
其機械運動方程為

式中: TL 是負載轉矩, B 是阻尼系數, J 是轉動慣量,ω 是電角速度。
2 永磁同步電機矢量控制系統
在dq 坐標系下,永磁同步電機的轉速和轉矩控制變為對電流分量isd 、isq 直接控制,采用isd = 0 ,使轉矩波動很小。
當定子電流在d 軸上的分量為0 時,電機電壓、磁鏈和轉矩方程為
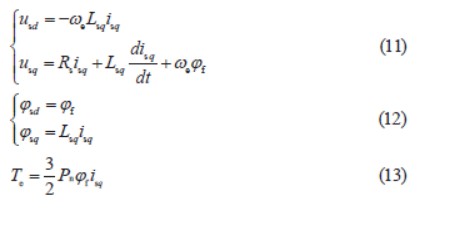
根據式(13) 可知電機的電磁轉矩Te 只與電流分量isq 有關。
圖1 是面裝式PMSM矢量控制系統圖,也是“電流-速度”雙閉環調速控制圖,提高了控制精度,減小誤差干擾。通過檢測轉子位置,來控制IGBT 開關管的開關狀態,使is 在d 軸上的分量為0,則輸出轉矩平穩。
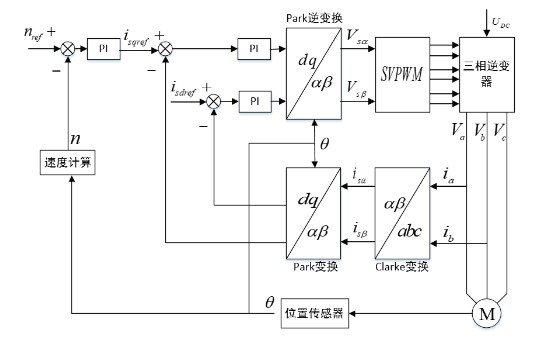
圖1 永磁同步電機矢量控制系統
轉速環將參考轉速1 500 r/min 和電機實際轉速比較,其轉速誤差經過速度PI 控制器,得到電流分量isq與實際電流比較,令isd=0。比例積分傳遞函數G(s) 為

式中:Kp、Ki 為比例和積分系數。
3 粒子群算法的控制器
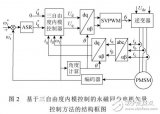
在仿真過程中,模型和參數會有所不同, 電機性能也會有所降低。在系統初始階段一般根據經驗微調PI參數,然后在PID 控制的基礎上引入PSO 控制器來調整PI 參數。粒子群算法在解空間中找到最優的粒子來實現PI 參數整定,具有較好的收斂速度和尋優精度,如圖2 是它的步驟圖。我們假設在K 維目標搜索空間中每n 個粒子構成一個種群,每個粒子以給定的速度尋找最佳位置,它會根據自己現在的位置和歷史上的最佳記錄位置來更新自己的位置,粒子群優化需要不斷更新粒子的速度和位置。
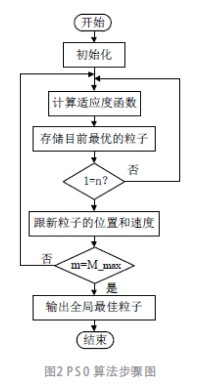
采用PSO 算法對PI 控制參數的優化,其中粒子L的當前/ 電流位置表示為:
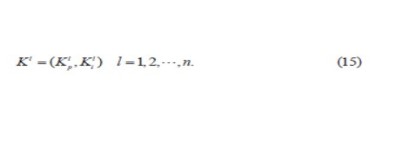
粒子L 的當前速度表示為:
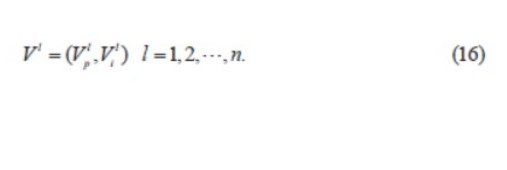
在其搜索歷史中粒子L 最佳位置為:
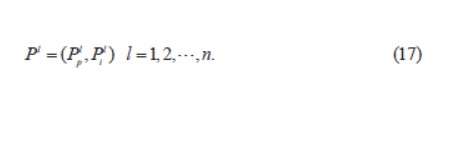
粒子在其搜索歷史中的最佳位置為:

通過以下公式更新速度和位置:
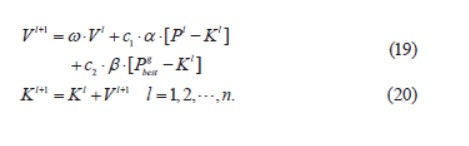
式中,α,β 是(0,1)的隨機數,ω 是恒定慣性權重,c1,c2 是學習因子。
4 仿真結果與分析
為了驗證粒子群算法比傳統PI 控制器優化效果跟好,搭建仿真模型,給出的仿真條件和電機參數如表1、2 所示。
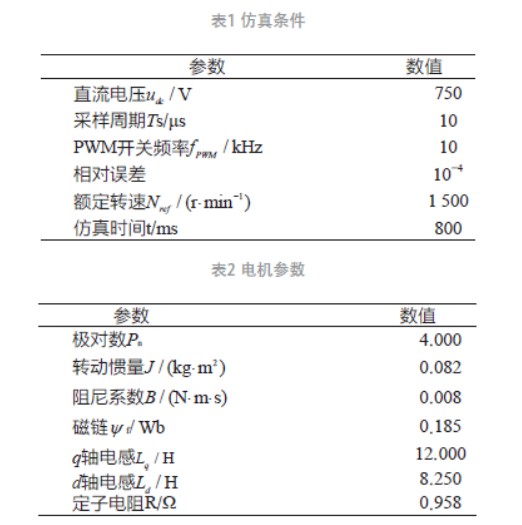
4.1 PMSM轉速仿真
轉速環PI 參數Kp1=0.14,Ki1=7;q 軸電流環PI參數Kp2=13.2,K12=1 053.8; d 軸電流環PI 參數Kp3-57.75,Ki3=1 053.8,圖3 是未采用粒子群算法的電機轉速波形。
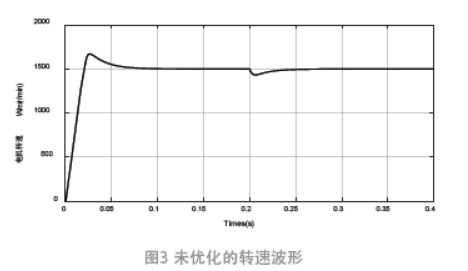
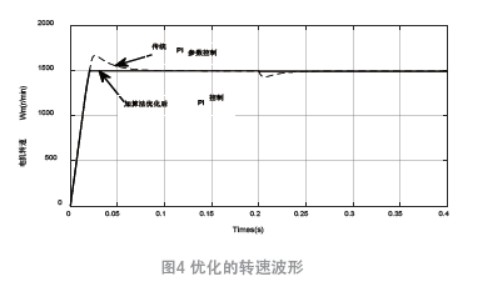
電機啟動0.06 s 后穩定到參考轉速1 500 r/min,且轉速超調量較高會縮短電機壽命。為了提高控制性能,通過粒子群算法得到更優PI 參數值是必需的。圖4 是粒子群算法控制器與傳統PIK 控制器仿真對比圖,從圖中可知,轉速穩定跟快,超調量幾乎為0。
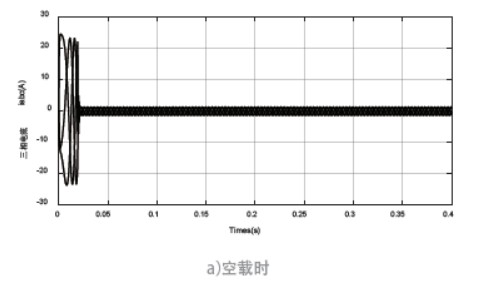
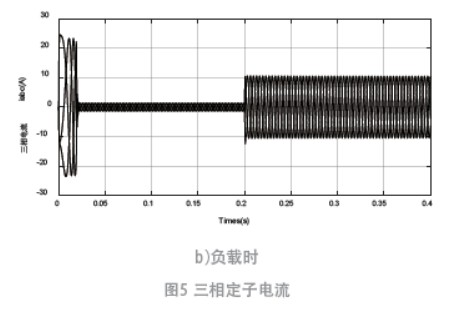
仿真模型空載和負載下仿真,圖5 是三相定子電流波形,由圖5a) 可知,空載啟動時電流脈動很快就穩定下來了。由圖5b) 可知,在0.2 s 時加入負載后,定子電流在0.03 s 才穩定下來,比空載時達到穩定用時更長。
仿真模型空載和負載下仿真,圖6 是電磁轉矩曲線。
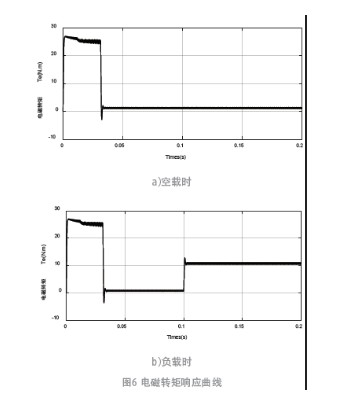
從圖6 可以看出,電機剛啟動時電磁轉矩有較小波動,空載條件下約0.03 s 時,電磁轉矩達到相對穩定,負載條件下約0.035 s 時,電磁轉矩與負載轉矩達到平衡,轉矩良好,說明抗干擾的能力較強。
綜合上述分析,當永磁同步電機參考轉速為額定轉速的情況下,無論是在空載條件下還是負載條件下運行,使用粒子群優化算法的控制效果明顯較好。
5 PMSM基本工況仿真
5.1 啟動特性仿真
首先,設置啟動轉速為1 500 r/min, 在0.2 s 加速到3 000 r/min,0.32 s 達到額定轉速。圖7 是電機轉速、三相定子電流和電磁轉矩仿波形。其中圖7a) 是從靜止啟動,0.07 s 時轉速穩定到了1 500 r/min,然后進行勻速運行。在0.2 s 時開始加速運行,大約0.32 s 時轉速穩定到3 000 r/min。
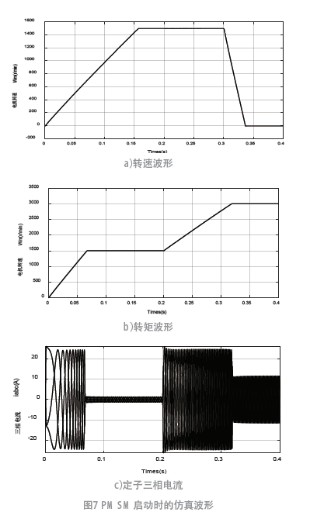
根據圖7c) 可知,在0.07 s 時三相定子電流幅值穩定到一固定值,在加速過程中也一樣,同時電磁轉矩曲線隨著轉速的穩定迅速穩定到0,從圖7b) 電磁轉矩仿真波形可知,電磁轉矩對負載轉矩響應良好,圖7 也能看出采用粒子群算法優化后波形要比傳統經驗獲得的PI參數得到的波形平穩很多。
6 制動特性仿真
由于地鐵車輛經常會啟動加速和制動減速頻繁等特點,良好的制動性能是地鐵車輛的一個重要標志。因此,制動性能的好壞體現了永磁同步電機穩定情況,采用調速方法的好壞,所以系統更需要良好的制動性能。地鐵啟動的參考轉速為1 500 r/min,負載轉矩15 N.m。在0.2 s時,設置負載轉矩突變為20 N.m;在0.3 s 時,設置參考轉速突變為0 進行制動。從圖8 可看出電機轉速沒有超調量,電磁轉矩和三相定子電流也跟隨轉速變化有良好的響應。
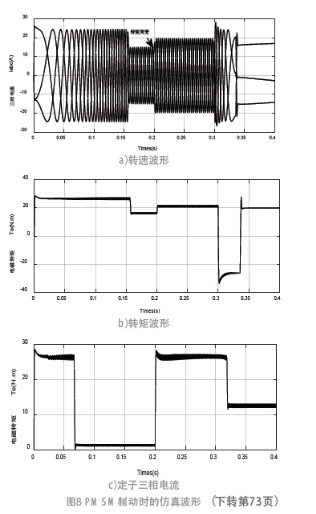
7 結論
本文研究了在地鐵車輛運行中,為了永磁同步電機轉速更好控制,采用“轉速- 電流”雙閉環、isd = 0 的矢量控制策略,在構建了矢量控制系統的基礎上增加了粒子群算話(PSO) 優化控制器參數的控制思想,并對地鐵車輛在不同工況下的啟動、制動性能,調速性能進行分析。根據仿真結果可知,通過采用粒子群算法優化控制系統PI 參數后,電機轉速的超調量幾乎為0 并快速穩定到參考轉速,電機輸出振蕩小,抗干擾能力強,得到了優化效果。
責任編輯:tzh
-
電流
+關注
關注
40文章
6891瀏覽量
132350 -
控制器
+關注
關注
112文章
16396瀏覽量
178512 -
電機
+關注
關注
142文章
9038瀏覽量
145737 -
地鐵車輛
+關注
關注
0文章
2瀏覽量
5974
發布評論請先 登錄
相關推薦




 地鐵車輛永磁同步電機矢量控制系統的設計方案
地鐵車輛永磁同步電機矢量控制系統的設計方案










評論