摘要:提出一種面向人臉表情識別的雙模板稀疏分類方法(DT-SRC)。該算法在用訓練樣本組成觀測矩陣的基礎上,通過添加正、負雙模板構造新的觀測矩陣,最后使用稀疏表示分類(SRC)進行識別。分別在JAFFE和CK人臉庫中進行驗證,結果表明,該算法識別準確率高,比SRC有更好的性能。
近幾年來,隨著MA Y[1-2]等人提出了基于稀疏表示分類的人臉識別,掀起SRC在人臉識別領域應用的熱潮。郝靜靜[3]等人提出一種改進的人臉識別方法,效果得到明顯提高。SALAH R[4]等人結合紋理特征提取和稀疏表示實現人臉表情的識別。Zhang Shiqing[5]等人把Gabor小波和局部二值化(LBP)分別用于表情特征提取,評估稀疏表示分類(SRC)的性能,并與支持向量機(SVM)、NSC、NNC等進行了比較。
MAHOOR H[6]等人對人臉運動單元進行稀疏表示實現表情識別,并與SVM、NSC方法進行了比較。但表情特征相對于人臉特征復雜,表情樣本少,加大了表情識別難度;直接運用SRC實現表情識別效果不是很好。鄒修國[7]等人把人臉識別系統應用到DSP,為識別系統廣泛應用奠定了基礎。
針對上述識別方法的優缺點,本文提出雙模板稀疏表示算法對人臉表情進行識別。通過增加正、負模板重構新的觀測矩陣,優化了稀疏表示的性能,減少噪聲、遮擋等對表情識別的影響,提高了表情的識別率。
1 基于稀疏表示的表情識別
1.1 稀疏表示理論
稀疏表示SR(sparse representation)可稱為壓縮感知,在很多領域扮演了越來越重要的角色。在式(1)中,稀疏表示理論的核心是在過完備矩陣D∈Rm×n下,重構出的
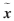
逼近原信號x,可理解為求解方程的過程:

在實際應用中,當m《

但式(2)的求解過程是一個NP-hard問題,計算效率極低。參考文獻[8]指出,在滿足約束等距性RIP的條件下,最小l1范數解逼近最小l0范數解。所以,可以在解集合尋找最小范數解(min‖x‖1)來代替求min‖x‖0,這是一個凸優化問題,用式(3)表示:
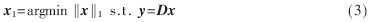
對于上述最優化問題,有許多l1算法[9]能夠有效地求解,包括正交匹配追蹤算法、LASSO、SPGL1算法等。
1.2 基于稀疏表示的表情識別算法
從表情庫中隨機取大部分人臉圖像作為訓練樣本,用于構建測試樣本對應的冗余字典。設第i類訓練樣本用矩陣表示為
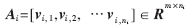
,每個圖像用v來表示。將k類共n個訓練樣本組合在一起形成整個訓練集矩陣D:
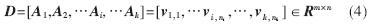
其中,m表示樣本的像素點,ni表示第i類樣本數目。通過求解出測試人臉在由訓練樣本構成的字典里的表示,可以知道測試人臉的表情類別信息。給出一個屬于第i類的測試樣本y,可以表示為:
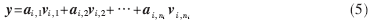
測試樣本僅用來表示自同一類訓練樣本的線性組合,其他類別的系數為零,即求解出的解x1=[0,0,…,0,
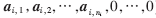
],只有第i類的值是非0元素。系數向量a中包含大量有利于分類的信息。判斷測試樣本所屬類別的公式為:

其中δi(x1)∈Rn,是第i組系數中非零的數為系數x1中與i對應的那些數。ri(y)=‖y-Aδi(x1)‖2表示的是y與Aδi(x1)的殘差值,認為殘差值最小的對應類別i為y的類別。
2 雙模板稀疏分類算法
實際應用中,訓練樣本個數和單樣本的像素點影響原信號重構的效果。直接用訓練樣本來構造冗余字典D,重構效率很低。由于圖像中含有噪聲干擾,為了解決噪聲的影響,式(1)改寫為:

其中,ε表示誤差向量,它與稀疏解x一樣含有大量的稀疏零點。因此,為了方便計算,把解x和ε合并起來,添加一個模板I去構造新的矩陣B,故y可以表示為:

其中,B=[D,I]∈Rm×(n+m)。由于m《(m+n),所以方程(8)一直是欠定方程,ω的解并不唯一。把矩陣I用單位矩陣表示,I的向量ii∈Rm中只含一個非零數,用來表示圖像中零散的噪聲點。單模板I通過向量e幫助x分擔原圖像的零散噪聲,使更多有用信息集中于向量x上。
原則上,觀測矩陣D在沒有限制的條件下,系數x可以為任何實數。然而,在識別的應用中,被識別的目標應該被訓練樣本用非負系數所表示。在訓練樣本庫中,尋找到類似測試樣本類別的個體時,主要集中于該類似樣本的非負系數上。然而,直接對上述的輔助稀疏x、e進行非負約束不太合理。因此,本文在正模板的基礎上提出了雙模板的擴展矩陣。如圖1所示,由訓練樣本矩陣、正模板和負模板共同構造雙模板的觀測矩陣。把測試樣本中可能存在的負值轉移到負模板,消除負系數對稀疏解x用于分類時的影響。此時,式(1)可寫為:

圖1 雙模板觀測矩陣
其中,e+∈Rm,e-∈Rm分別為正輔助系數和負輔助系數向量,新觀測矩陣
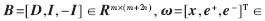
Rn+2m是非負系數向量。此時,負模板-I中的每一列向量-ii只含有一個零值,與正模板的ii剛好相反,可以減少稀疏表示中對n的要求,解決樣本數不夠的問題。式(8)的矩陣B中m《2m+n,因此是欠定方程,且ω沒有唯一的解。通過變換域把式(8)求解問題轉化為l1-正則化最小平方問題,稀疏表達式表示為:

其中‖·‖1和‖·‖2分別表示l1和l2范數。本文使用l1范數解法l1_ls求稀疏解x。然后把稀疏解x代入式(6),求出殘差值,即可得到測試樣本y對應的類別。
對于一個有效的測試人臉,所求的非零系數集中于單個訓練目標。為了衡量觀測矩陣的性能,參考文獻[4]定義稀疏集中指數(SCI)來測量稀疏系數集中程度:
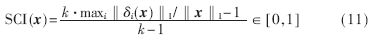
如果
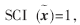
則測試樣本只用一個目標樣本來表示;如果
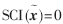
,則測試樣本的稀疏表示均勻地分布在所有樣本中。
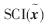
的值越大,說明求解的x稀疏性越好。本文將通過衡量SCI指數比較DT-SRC和SRC的性能。
3 實驗及結果分析
3.1 JAFFE人臉數據庫上的實驗
對人臉庫的圖像進行幾何歸一化、灰度歸一化、濾波等預處理。JAFFE人臉圖像經過預處理后大小為64×64,如圖2所示,從左到右依次為憤怒、厭惡、恐懼、開心、自然、傷心、驚奇7種表情。

圖2 KA的7種表情預處理后的圖像
把JAFFE人臉庫的210張圖片按7種表情進行分類,每人每種表情隨機抽取一個作為測試樣本,其他為訓練樣本。對人臉圖像進行下采樣降維,針對SRC和DT-SRC算法選擇最優的下采樣率,采樣點為15×7,比較NSC、SRC和DT-SRC的識別性能。
表1中平均SCI指數為統計70個測試人臉的每個SCI指數后求平均值,它能反映出稀疏表示分類的識別性能。從表1可以看出,DT-SRC相對SRC和NSC在識別率上有很大的提升,但犧牲了一定的時間;SRC和NSC的識別率差不多。
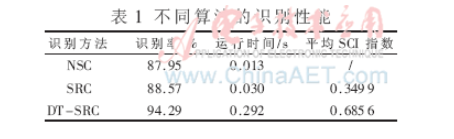
圖3中,SCI指數的范圍為[0,1],指數越接近1,所求得的解越稀疏,稀疏性越好。從圖3可以看出,在第12、50個測試樣本時SCI都很低,可以認為這些樣本類別不能很好地被識別,所含的表情分類信息不明顯;DT-SRC的SCI指數普遍比SRC的高,則DT-SRC的重構效果比SRC有了很大的提高。
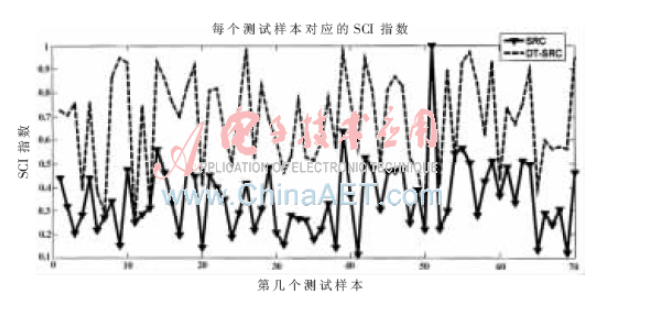
圖3 JAFFE的測試人臉在SRC、DT-SRC的SCI指數
本文取圖3的第70個測試人臉圖,列出該圖在DT-SRC和SRC下的殘差值,如圖4所示。圖4(a)為第70個人臉的裁剪圖,圖4(b)和圖4(c)中的橫坐標1~7分別表示憤怒、厭惡、恐懼、開心、自然、傷心、驚奇的7種表情。圖4(b)、圖4(c)的第7個方柱(驚奇)的殘差值最低,可以判斷出圖4(a)的類別是驚奇,該人臉的表情是驚奇。
從圖4可以看出,DT-SRC的第7類表情殘差值相對其他類表情要明顯,所求解的系數x在表情類別中主要集中于驚奇處。圖4(b)中最低兩個殘差值的比例大約為1 400/100=14:1;圖4(c)中最低兩個殘差值的比例大約為500/200=5:2;在該測試人臉的識別中,DT-SRC算法比SRC有更好的稀疏性和分類效果。
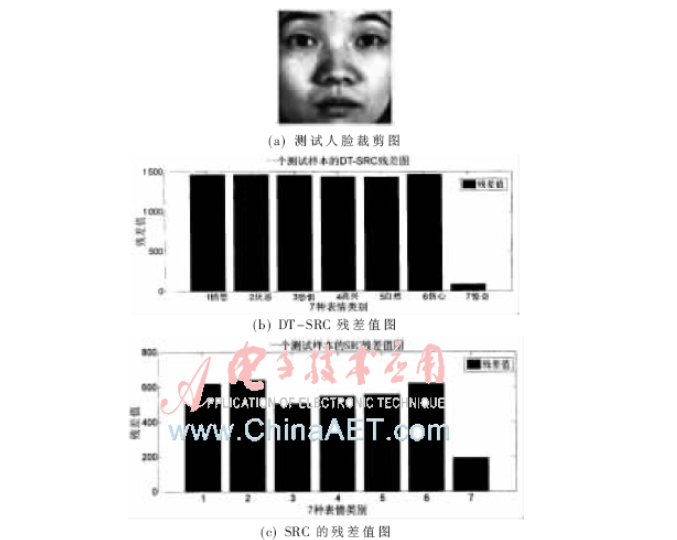
圖4 某個測試人臉的殘差值圖
3.2 在CK人臉數據庫上的實驗
3.1節實驗同樣適用于Cohn-Kanade(CK)表情庫。選取裁剪成64×64的CK人臉庫作為實驗數據庫,把其中一人的7種表情顯示如圖5所示,從左到右依次為厭惡、恐懼、開心、自然、傷心、驚奇、憤怒7種表情。

圖5 CK的7種表情預處理后的圖像
CK庫有18個人,每個人每種表情有5張,有7種表情,共有630張圖像。每人每種表情隨機抽取一個作為測試樣本,其他為訓練樣本,則總有126張測試樣本、504張訓練樣本。然后比較NSC、SRC、ISRC 3種算法的識別率,實驗結果如表2所示。計算每張CK測試人臉在SRC、DT-SRC識別后的SCI指數,126張測試人臉的SCI指數如圖6所示。
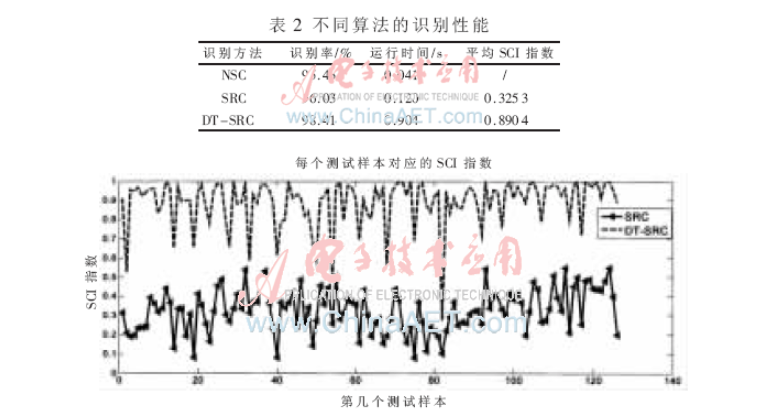
圖6 CK的測試人臉在SRC、DT-SRC的SCI指數
分析表1和表2可知,SRC和NSC在識別時間上比其他方法有絕對的優勢,而且識別率也較好。在CK庫中的識別率明顯比JAFFE庫好,這是因為所使用的CK庫的圖片質量好,各表情差異明顯。DT-SRC比SRC和NSC在識別率方面有所提高,特別是在圖片表情特征不明顯的情況下,識別率能有很大的提高。其實,在CK庫中所使用訓練樣本比較多,SRC算法能達到很高的識別率。
但在JAFFE庫里,由于表情庫的樣本不多,導致字典D的列數不夠,不能充分發揮出稀疏表示的作用,從而導致它的識別率低。而本文的算法DT-SRC彌補了字典矩陣D列數不足的缺點,且降低了噪聲和負系數的影響,使識別率得到提高,但犧牲了一定的運算時間。
從圖3和圖6的SCI指數圖看出,DT-SRC的SCI總體上比SRC的高,DT-SRC的稀疏表示性比SRC的好。當測試樣本不是有效的人臉時,DT-SRC能更好地排除該張圖片,減少錯誤的判斷。
本文提出的DT-SRC實用性強、效率高,降低了識別的復雜度,解決了SRC用于表情識別時效率不高的問題。通過SRC與DT-SRC的比較,發現字典矩陣D的構造影響著正確識別率和稀疏分類性能,D中的元素能最大程度地表示測試樣本的結構,且所添加的正、負模板可消除噪聲、負系數等影響。因此,DT-SRC在表情識別方面效果不錯。
參考文獻
[1] WRIGHT J, YANG A Y, MA Y,et al. Robust face recognition via sparse representation[J]。 Pattern Analysis and Machine Intelligence, 2009,31(2):210-217.
[2] JIA K,CHAN T H,MA Y. Robust and practical face recognition via structured sparsity[C]。 European Conference on Computer Vision(ECCV), 2012:331-344.
[3] 郝靜靜,李莉。一種基于KPCA與LDA的人臉識別改進算法[J]。電子技術應用,2013,39(12):132-134.
[4] SALAH R, KHOLY A E, YOUSSRI M. Robust facial expression recognition via sparse repre-
sentation and multiple gabor filters[J].International Journal of Advanced Computer Sciences and Applications, 2013,4(3):82-87.
[5] Zhang Shiqing, Zhao Xiaoming, Lei Bicheng. Robust facial expression recognition via compressive sensing[J].Sensors, 2012,12(12):3747-3761.
[6] MAHOOR H, ZHOU M, KEVIN L,et al. Facial action unit recognition with sparse representation[C].Automatic Face & Gesture Recognition and Workshops(FG2011), 2011:336-342.
[7] 鄒修國, 李林, 陸靜霞。 基于DSP的人臉HU矩識別研究[J]。電子技術應用,2013,38(11):150-153.
[8] CAND?魬S E J, WAKIN M B. An introduction to compressive sampling[J]。 Signal Processing Magazine,2008,25(2):21-30.
[9] YANG A, GANESH A, MA Y,et al. Fast L1-minimization algorithms for robust face recognition[J]。 IEEE Transactions on Image Processing(TIP), 2013,22(8):3234-3246.
編輯:jq
-
SVM
+關注
關注
0文章
154瀏覽量
32503 -
人臉識別
+關注
關注
76文章
4012瀏覽量
82047 -
SRC
+關注
關注
0文章
61瀏覽量
18010 -
NNC-
+關注
關注
0文章
2瀏覽量
21131
發布評論請先 登錄
相關推薦
開源六軸協作機器人myCobot 320結合人臉表情識別情緒!

基于Python的深度學習人臉識別方法
人臉識別技術的可行性在于矛盾具有什么性
人臉檢測和人臉識別的區別是什么
人臉檢測與識別的方法有哪些





 淺談面向人臉表情識別的雙模板稀疏分類方法
淺談面向人臉表情識別的雙模板稀疏分類方法










評論