做過運動控制的小伙伴都知道，S曲線很重要，下面一張動圖對比一下，你就知道S曲線的好處：

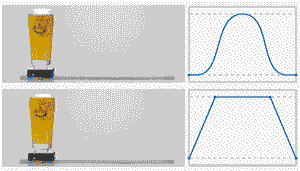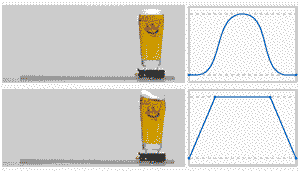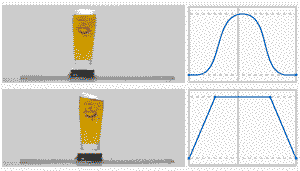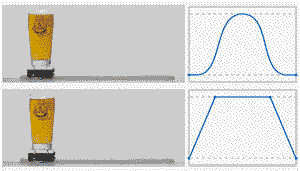
下面分享一下S曲線的內容：

1 前言

S形加減速的最重要特征是該算法的加速度/減速度曲線的形狀如字母 S。S形加減速的速度曲線平滑 ，從而能夠減少對控制過程中的沖擊，并使插補過程具有柔性 ［^1］。由于T形曲線在加速到勻速的切換過程中，實際中存在較大過沖，因此這里對比一下T曲線和7段S曲線的實際過程；

T形：加速 -》 勻速 -》 減速

S形：加加速（） -》 勻加速（） -》 減加速（）-》 勻速（）-》 加減速（）-》 勻減速（）-》 減減速（）

上文在加速這塊的文字描述可能讀起來起來有點繞，下面看圖：

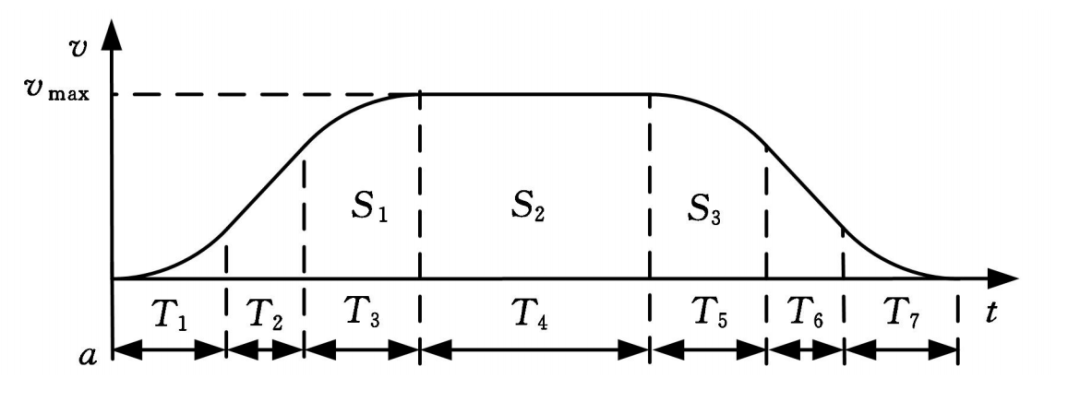
2 理論

分析由于S曲線在加減速的過程中，其加速度是變化的，因此這里引入了新的一個變量 ，即加加速度。

因此對應上圖的7段S速度曲線中，規(guī)定最大加速為，最小加速度為，則加速度的關系；

加加速（）：逐漸增大；

此時

勻加速（）：達到最大；

此時

減加速（）：逐漸減小；

此時

勻速（）：不變化；

此時

加減速（）： 逐漸增大；

此時

勻減速（）： 達到最大；

此時

減減速（）： 逐漸減小；

此時

“為加速度的絕對值；其中

所以通常需要確定三個最基本的系統(tǒng)參數(shù) ：系統(tǒng)最大速度 ，最大加速度a_{max} ，加加速度，就可以可確定整個運行過程［^2］ ；

最大速度：反映了系統(tǒng)的最大運行能力 ；

最大加速度：反映了系統(tǒng)的最大加減速能力 ；

加加速度：反映了系統(tǒng)的柔性；

柔性越大，過沖越大，運行時間越短；

柔性越小，過沖越小，運行時間越長；

2.1 加速度時間關系方程

整個加速度變化的過程具體如下圖所示；

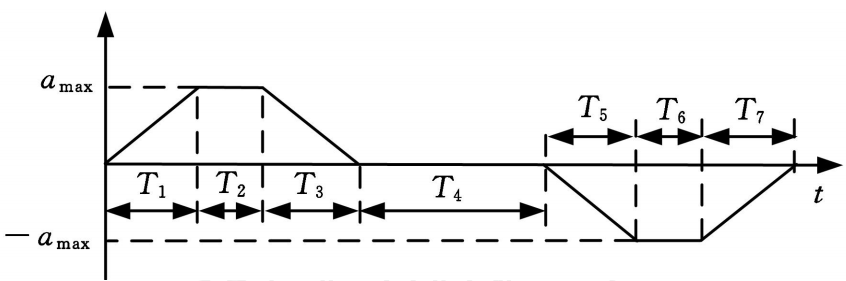
再次強調一下 和 的關系，另外這里再引入變量 ，

比如，當前時刻 ，即 位于區(qū)間 ，則如果將 作為初始點，則 為 相對于時刻的時間，則有：

下面可以得到加速度與時間的關系函數(shù)，具體如下：

根據(jù) ① 式，將 代入 ② 式可以得到：

上式中 ；

2.2 速度時間關系方程

速度和加速度滿足 ；加加速度和速度的關系滿足：

結合加速度時間關系并結合② 式可以得到速度曲線關系，具體關系如下圖所示；

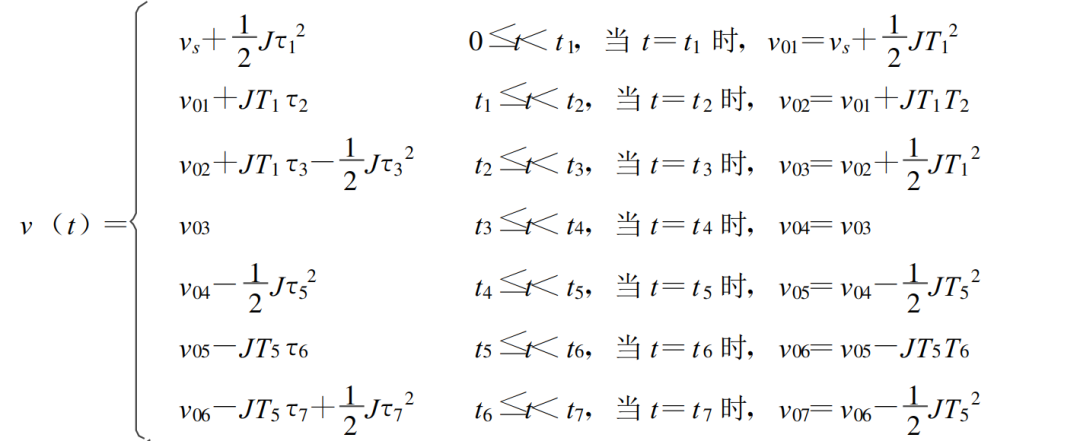
進一步簡化可以得到：

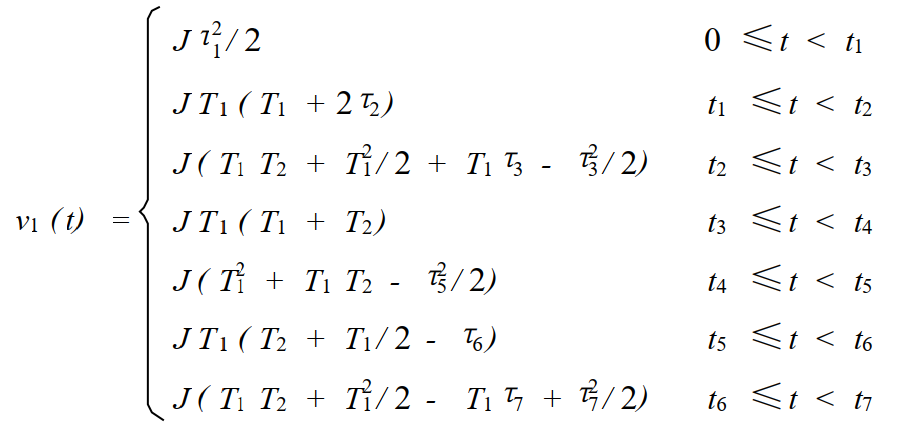
2.3 位移時間關系方程

位移 和加加速度 直接滿足關系如下：

簡單推導

因此可以得到：

“積分忘的差不多了，回去再復習一下；

最終位移的方程如下所示；

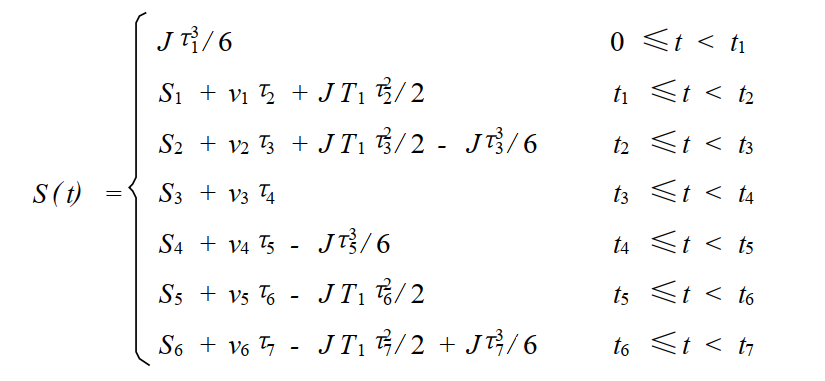
3 程序實現(xiàn)的思路

正如前面所提到的，S曲線規(guī)劃需要確定三個最基本的系統(tǒng)參數(shù) ：系統(tǒng)最大速度 ，最大加速度a_{max} ，加加速度，這樣就可以確定這個運行過程。這里有一個隱性的條件，就是在運行的過程中可以達到最大速度，這樣才是完整的7段S曲線，另外這里還有一些中間參數(shù)：

，因此有 ；

加加速度 ；

；

，用戶給定整個運行過程所需要的時間；

但是通常實際過程中關心，，；

3.1 推導

理想狀態(tài)假設存在 和，則推導過程如下：

因此可以得到：

簡化之后得到：

根據(jù)②式可知：

最終得到：

下面可以根據(jù)位移時間關系方程進行離散化的程序編寫。

假設可以到達最大速度，且用戶給定了整個過程運行時間，則 的推導如下：

簡化上式可以得到：

根據(jù) 代入上式可得：

3.2 的推導

這時候還剩下需要計算，通過已量 可以推導出來；首先位移之間滿足關系如下：

其中加速區(qū)長度為 ；其中減速區(qū)長度為 ；

具體推導；［^2］前面提到過，，因此在=0的時候，則

這里簡單推導一下：

根據(jù)④，⑤最終簡化得到：

“：為運行的總時間：為運行的總路程

詳細推導過程如下：

因為：

因為：

所以，簡化得到：

所以可以得到：

因為：

將其代入可以得到：

簡化得到最終結果：

4 matlab

程序matlab程序親測可以運行，做了簡單的修改，因為這里直接給定了整個運行過程的時間，所以需要在SCurvePara函數(shù)中求出加加速度 的值，路程為 1：

SCurvePara

function ［Tf1，V，A，J，T］ = SCurvePara（Tf， v， a）

T = zeros（1，7）;

for i=1:1000

% 加加速度 J

J = （a^2 * v） / （Tf*v*a - v^2 - a）;

% Tk

T（1） = a / J;

T（2） = v / a - a / J; % t2 = v / a - t1;

T（3） = T（1）;

T（4） = Tf - 2 * a / J - 2 * v / a; % t4 = Tf - 4*t1 - 2*t2;

T（5） = T（3）;

T（6） = T（2）;

T（7） = T（1）;

% 根據(jù)T2和T4判斷S曲線的類型

if T（2） 《 -1e-6

a = sqrt（v*J）;

display（‘t2《0’）;

elseif T（4） 《 -1e-6

v = Tf*a/2 - a*a/J;

display（‘t4《0’）;

elseif J 《 -1e-6

Tf = （v^2 + a） / （v*a） + 1e-1;

display（‘J《0’）;

else

break;

end

end

A = a;

V = v;

Tf1 = Tf;

end

SCurveScaling

function s = SCurveScaling（t，V，A，J，T，Tf）

% J = （A^2 * V） / （Tf*V*A - V^2 - A）;

% T（1） = A / J;

% T（2） = V / A - A / J; % T（2） = V / A - T（1）;

% T（3） = T（1）;

% T（4） = Tf - 2 * A / J - 2 * V / A; % T（4） = Tf - 4*T（1） - 2*T（2）;

% T（5） = T（3）;

% T（6） = T（2）;

% T（7） = T（1）;

%%

if （t 》= 0 && t 《= T（1））

s = 1/6 * J * t^3;

elseif （ t 》 T（1） && t 《= T（1）+T（2） ）

dt = t - T（1）;

s = 1/2 * A * dt^2 + A^2/（2*J） * dt.。.

+ A^3/（6*J^2）;

elseif （ t 》 T（1）+T（2） && t 《= T（1）+T（2）+T（3） ）

dt = t - T（1） - T（2）;

s = -1/6*J*dt^3 + 1/2*A*dt^2 + （A*T（2） + A^2/（2*J））*dt 。..

+ 1/2*A*T（2）^2 + A^2/（2*J）*T（2） + A^3/（6*J^2）;

elseif （ t 》 T（1）+T（2）+T（3） && t 《= T（1）+T（2）+T（3）+T（4） ）

dt = t - T（1） - T（2） - T（3）;

s = V*dt 。..

+ （-1/6*J*T（3）^3） + 1/2*A*T（3）^2 + （A*T（2） + A^2/（2*J））*T（3） + 1/2*A*T（2）^2 + A^2/（2*J）*T（2） + A^3/（6*J^2）;

elseif （ t 》 T（1）+T（2）+T（3）+T（4） && t 《= T（1）+T（2）+T（3）+T（4）+T（5） ）

t_temp = Tf - t;

dt = t_temp - T（1） - T（2）;

s = -1/6*J*dt^3 + 1/2*A*dt^2 + （A*T（2） + A^2/（2*J））*dt 。..

+ 1/2*A*T（2）^2 + A^2/（2*J）*T（2） + A^3/（6*J^2）;

s = 1 - s;

elseif （ t 》 T（1）+T（2）+T（3）+T（4）+T（5） && t 《= T（1）+T（2）+T（3）+T（4）+T（5）+T（6） ）

t_temp = Tf - t;

dt = t_temp - T（1）;

s = 1/2 * A * dt^2 + A^2/（2*J） * dt + A^3/（6*J^2）;

s = 1 - s;

elseif （ t 》 T（1）+T（2）+T（3）+T（4）+T（5）+T（6） && t 《= T（1）+T（2）+T（3）+T（4）+T（5）+T（6）+T（7） + 1e5 ）

t_temp = Tf - t;

s = 1/6 * J * t_temp^3;

s = 1 - s;

end

end

測試的代碼如下：TEST

%%

N = 500;

ThetaStart = 0; %起始位置

ThetaEnd = 90; %最終位置

VTheta = 90; %1 速度

ATheta = 135; %1.5 加速度

Tf = 1.8; % 總行程時間

v = VTheta/（ThetaEnd - ThetaStart）;

a = ATheta/（ThetaEnd - ThetaStart）;

v = abs（v）;

a = abs（a）;

Theta = zeros（1，N）;

s = zeros（1，N）;

sd = zeros（1，N）;

sdd = zeros（1，N）;

［TF，V，A，J，T］ = SCurvePara（Tf， v， a）;

display（J， ‘J：’）;

display（TF，‘Tf：’）;

display（V，‘v：’）;

display（A， ‘da：’）;

display（TF-Tf，‘dTf：’）;

display（V-v，‘dv：’）;

display（A-a， ‘da：’）;

t=linspace（0，TF，N）;

dt = t（2） - t（1）;

for i = 1:N

if i == N

a = a;

end

s（i） = SCurveScaling（t（i），V，A，J，T，TF）;

Theta（i） = ThetaStart + s（i） * （ThetaEnd - ThetaStart）;

if i》1

sd（i-1） = （s（i） - s（i-1）） / dt;

end

if i》2

sdd（i-2） = （sd（i-1） - sd（i-2）） / dt;

end

end

subplot（3，1，1）;

legend（‘Theta’）;

xlabel（‘t’）;

subplot（3，1，1）;

plot（t，s）

legend（‘位移’）;

xlabel（‘t’）;

title（‘位置曲線’）;

subplot（3，1，2）;

plot（t，sd）;

legend（‘速度’）;

xlabel（‘t’）;

title（‘速度曲線’）;

subplot（3，1，3）;

plot（t，sdd）;

legend（‘加速度’）;

xlabel（‘t’）;

title（‘加速度曲線’）;

看到最終仿真結果和預期相同；

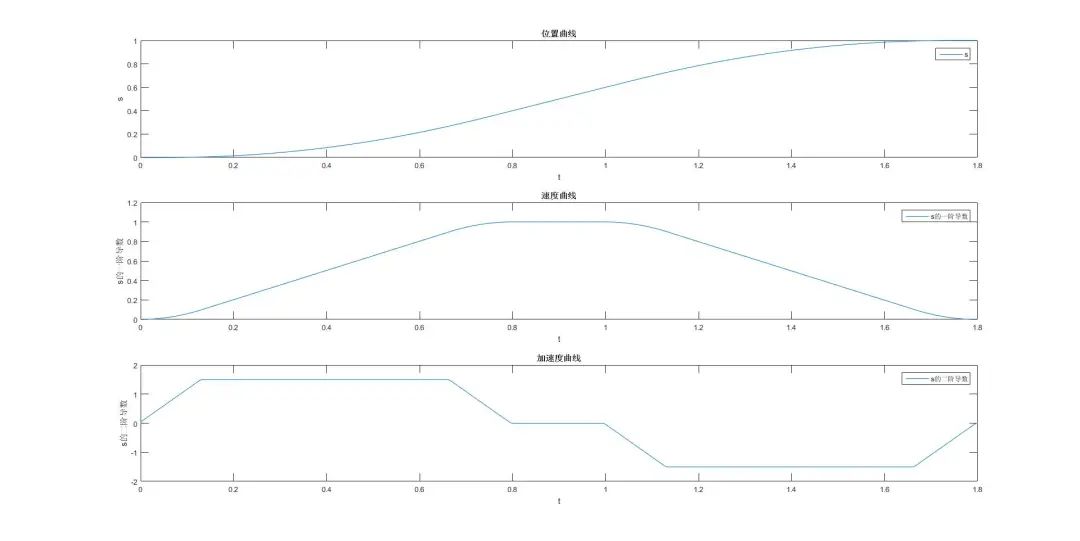
最后再看一下T形和S形速度曲線規(guī)劃的效果對比：

5 總結

本文只對7段的S曲線規(guī)劃做了詳細的推導和介紹，matlab中的程序對于4段和5段都有做實現(xiàn)，很多是在理想情況下進行推導的，初始速度默認為0，終止速度也為0，并且假設加減速區(qū)域相互對稱。最終運行結果符合預期效果。

“文中難免有錯誤和紕漏之處，請大佬們不吝賜教創(chuàng)作不易，如果本文幫到了您；

6 參考

［^1］：陳友東 魏洪興 王琦魁。數(shù)控系統(tǒng)的直線和 S 形加減速離散算法［D］。北京：中國機械工程，2010.

［^2］：郭新貴 李從心 S 曲線加減速算法研究 上海交通大學國家模具 CAD 工程研究中心 ， 200030
編輯：lyn