學習數字信號處理的訣竅:復數或向量的運用
學好數字信號處理的訣竅之二——復數與向量的運用
信號的相位為什么很重要
一、學好數字信號處理的訣竅之二——復數和向量的運用 在學習復數之前,我們學過的實數可以稱為一元數,它只有一個維度,即大小。復數是二元數,它有兩個維度,即實數部分和虛數部分,也可以說幅度和相位角。由于復數的維度比實數多一個,因而得到很多精彩的應用。(順便介紹一下,三元數是不存在的,但是英國數學家哈密爾頓發明了四元數,后來的一些數學家陸續發明了八元數、十六元數,但隨著元數的增加,其應用價值微乎其微。) 向量是一種既有大小又有方向的量,是和標量相對的,向量在現實中是廣泛存在的,復數處理這種既有大小又有方向的量即向量時,表現出極大的簡潔性。復數和向量在信號分析和處理中可以使復雜問題簡單化、直觀化,是理解數字信號處理非常有力的工具。此外,復數在表示既有一定大小、又有一定相位的量如正弦信號時,表現出很大的優越性。
復數的用途表現在它同時包含了向量的幅度和相位信息,因而給計算和公式的表達帶來很大的方便。復數是工程中最強大的工具之一,可以這么說,沒有復數這種工具,近代工業文明簡直是不可想象的。下面舉幾個例子說明復數的應用。 1、傅里葉變換。沒有復數作為工具,周期信號分解的表達式將會比較復雜,而用復數表達則異常簡潔、美觀,便于數學分析。 高等數學講過傅里葉級數的內容,連續周期信號f(t)可以展開為無窮級數,設f(t)的周期為T,則角頻率為Ω = 2π/T,可以分解為:
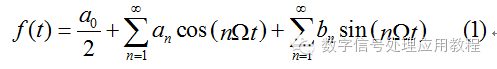
式中的系數an(n = 0, 1, 2,…), bn(n = 1, 2, …)分別為:
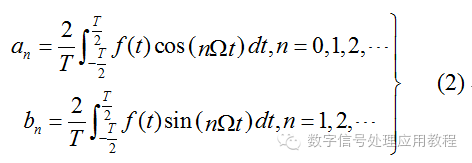
上面的表達式物理意義很明確,但是計算很繁瑣,并且在實際中無需區分頻率相同的正弦和余弦信號,因為同頻的正弦和余弦信號之和還是同頻的信號,只是幅度和相位發生了改變(下面將談到信號的相位的重要性)。《信號與系統》里面引進復指數形式的信號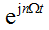 后,上面的公式(1)和(2)簡化為: ? ?
后,上面的公式(1)和(2)簡化為: ? ?
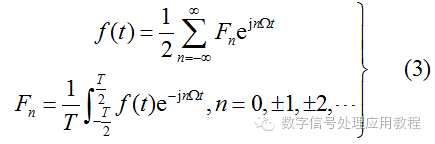
直觀上看,公式(3)比公式(1)和(2)之和要簡潔很多,它們包含的信息量是完全一樣的,但是式(3)更方便進行數學分析。 2、系統函數。利用復數可以很方便地表示信號經過一個系統(模擬的或數字的)之后各個頻率成分的變化情況,因為系統不僅改變輸入信號各個頻率分量的幅值大小,也改變相對相位的大小,而信號的相位是很重要的物理量,該系統稱為濾波器,可以實現各種功能。沒有復數作為工具,對系統的變換特性進行描述是極其困難的。 下面是一個有趣的問題:某人向東走1公里后,向左拐走1/2公里,再向左拐走(1/2)2公里,……,如此不停地進行下去,問這個人最后停留在什么位置? 用復數解決很簡單,初始位置到最后停留位置連線的復數為
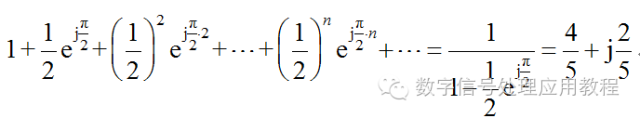
即某人最終位于起始位置的偏東4/5公里、偏北2/5公里的位置。很多同時涉及距離和角度的題目用復數解決都很簡單,復數在中學競賽中也得到重要應用。 二、為什么信號的相位很重要 任何信號(周期或非周期,連續或離散)都可以分解為不同頻率的余弦信號加權和。余弦信號由三個參數確定:幅度、相位和頻率,這三個參數的地位是同等重要的,相位的重要性可以通過以下幾個具體例子看出來。
1、兩個同頻率的余弦信號相互疊加,當相位相同時將互相加強,一個實際的例子是,當部隊過大橋時,為了避免走正步的頻率和大橋的固有頻率同相而加強,導致共振破壞大橋,因此部隊過大橋時都走碎步;當兩個同頻余弦信號相位正好相反時,將互相減弱,甚至可以抵消為零。兩個同頻信號的疊加,相對相位的不同將導致結果差異很大。 2、國慶典禮上軍人的步伐高度一致,給人一種難以言說的美感和震撼感,從數學上來說就是“相位”高度一致。 3、有一句諺語“海上無風三尺浪”,這是因為海上不同的船只都獨立產生一個類似余弦波,很多的波合成時,在某些相對相位情況下互相疊加而加強。
4、一個信號的不同頻率成分,經過一個系統之后,如果相對“相位”發生了改變,即有的頻率成分“超前”了,有的頻率成分“落后”了,那么合成之后的信號就會發生失真,而很多情況是要求信號不失真地傳輸的,如圖像信號等。當然,有時對信號進行有目的“失真”處理也是必要的,比如將含有噪聲的信號進行去噪。 總之,掌握好復數和向量,是學好數字信號處理等課程的一個訣竅,這是由復數可以同時表示幅度和相位的性質決定的。
原文標題:學好數字信號處理的訣竅之二——復數和向量的運用
文章出處:【微信公眾號:數字信號處理輔導】歡迎添加關注!文章轉載請注明出處。
責任編輯:haq
-
數字信號
+關注
關注
2文章
973瀏覽量
47589
原文標題:學好數字信號處理的訣竅之二——復數和向量的運用
文章出處:【微信號:digital_signals,微信公眾號:數字信號處理輔導】歡迎添加關注!文章轉載請注明出處。
發布評論請先 登錄
相關推薦




 數字信號處理的相位為什么很重要?
數字信號處理的相位為什么很重要?










評論