據劍橋大學和俄羅斯斯科爾科沃科技學院的研究人員稱,通過將光信號相乘,可以解決一系列具有挑戰性的計算問題,這一方法可以應用于圖論、神經網絡、人工智能和代碼糾錯中。
在《物理評論快報》(Physical Review Letters)上發表的一篇論文中,他們提出了一種新型的計算方式——乘法,可以顯著減少所需的光信號數量,同時簡化對最佳數學解決方案的搜索,從而實現超高速光學計算機,徹底改變模擬計算。
與傳統的使用電子的計算機不同,光子計算使用由激光或二極管產生的光子進行計算。由于光子基本上沒有質量并且可以比電子傳播更快,因此光學計算機將更加節能,并能夠通過多時空光學通道同時處理信息。
光學計算機中的計算單元由光信號的連續相位表示,通常是將來自兩個不同光源的光波相加,然后將結果映射到「0」或「 1」的狀態來實現計算。
但是,現實生活中存在高度非線性的問題,其中多個未知數在進行乘法運算時會改變其他未知數的值。在這種情況下,以線性方式組合光波的傳統光學計算方法將失效。
近日,劍橋大學應用數學和理論物理系的納塔利婭·貝洛夫(Natalia Berloff)教授以及斯科爾科沃科學技術學院的博士生尼基塔·斯特羅耶夫(Nikita Stroev)發現,光學系統可以通過將描述光波的波函數相乘而不是相加的方式來組合光波,這可能是另一種不同類型的表示光波之間連接的方式。
圖|光學微腔中的極化子
(來源:The University of Sheffield)
他們使用稱為電磁極化子的準粒子(半光半物質)闡明了這一現象,同時將這一思想擴展到了更大的光學系統類別,例如光纖中的光脈沖。由于極化子的物質組成,相干的、超快速移動的極化子可以在空間中產生微小脈沖或粒子,并以非線性的方式相互重疊。
Stroev說:「我們發現,關鍵要素是如何將脈沖彼此耦合。如果正確地實現了耦合和相應的光強度,光就會成倍增加,從而影響單個脈沖的相位,給出問題的答案。這樣就可以用光來解決非線性問題。」
在這些光學系統的每一個元件中,用于確定光信號相位的波函數乘法或來自于自然發生的非線性或來自于引入的外部系統的非線性。
令人驚訝的是,不需要將連續的光相位映射到解決二進制變量問題所必需的0、1狀態上。相反,系統傾向于在尋找最小能量配置的末尾帶來這些狀態。這是通過將光信號相乘得到的屬性,而以前的光學機器需要共振激勵才能在外部將相位固定為二進制值。
作者還提出并實現了一種方法,可以通過臨時更改信號的耦合強度來引導系統給出解決方案。
我們將要開始確定可以通過專用物理處理器直接解決的不同類型的問題,高階二進制優化問題就是這類問題之一,光學系統可以非常有效地解決它們。
與現代電子計算機相比,光學計算要證明其在解決難題上的優越性還需要解決許多挑戰:降噪、糾錯、改進的可伸縮性、將系統引導到真正的最佳解決方案。
通過改變框架來直接解決不同類型的問題,可能會使光學計算機更接近解決傳統計算機無法解決的現實問題。
原文標題:讓光信號做乘法?
文章出處:【微信公眾號:驛路通】歡迎添加關注!文章轉載請注明出處。
責任編輯:haq
-
人工智能
+關注
關注
1804文章
48406瀏覽量
244662 -
光信號
+關注
關注
0文章
455瀏覽量
28019
原文標題:讓光信號做乘法?
文章出處:【微信號:gh_7d4f9e0f2bd8,微信公眾號:驛路通】歡迎添加關注!文章轉載請注明出處。
發布評論請先 登錄
相關推薦
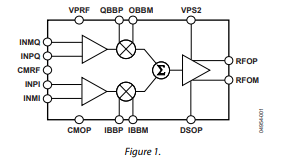
ADL5390 RF矢量乘法器技術手冊
Verilog中signed和$signed()的用法
ADS1247采集熱電偶信號數據不穩的原因?
CAN通信節點多時,如何減少寄生電容和保障節點數量?

ADS1118測量4-20mA和0-5V信號數據,有點跳動也有點誤差,怎么解決?
afe4900在測量的PPG信號比較弱的時候,有時取到的環境光信號是負的,怎么處理?
PLC模擬量信號數據采集如何實現



















評論