在上一個系列“超越局域近似-費曼圖展開(1)”中,我們看到了高階頂角函數對于自能修正的神奇之處。通過將不同格點上的局域兩粒子頂角函數用非局域項連接起來,我們可以得到對于動力學平均場局域自能的非局域修正。這讓我們對于頂角函數的作用有了新的認識和理解。頂角函數不再只是作為Bethe-Salpeter方程中的一部分,總是與各種極化率綁定在一起。高階頂角函數與低階頂角函數之間的關系,讓我們多了一種構造量子多體理論的途徑。今天,我們來進一步聊聊兩粒子頂角函數的有趣之處。
我們首先來介紹一下兩粒子格林函數。和單粒子格林函數類似,它代表的是多粒子體系對于增加和減少兩個粒子的響應,可以依照單粒子格林函數的樣子類似定義
這里我們用1,2,3,4表示一系列聯合指標,可以包括動量、自旋等。如果作用量S是無相互作用的,我們可以對四費米算符應用Wick分解,分別得到兩個單粒子傳播子的乘積,
然而,如果S含有相互作用項時,就會多出一項,對應的是4費米子不可分的收縮項。
我們對單粒子格林函數很熟悉,知道它有兩個外腳,其他部分對應自能的貢獻。
相應的,我們可以理解,兩粒子格林函數應該有四個外腳,同時還有類似于自能一樣的東西,如下圖所示。
這三項,分別對應了上述公式中兩粒子格林函數的三個貢獻。其中,陰影部分的圖形是兩粒子格林函數的“自能”部分,我們通常稱之為完全頂角函數(full vertex function)。這里我們沒有畫成類似于單粒子格林函數Dyson方程那樣的迭代方式,而是把它收縮成一個整體。這是因為兩粒子層次上的“Dyson方程”形式上變得比較復雜了,還需要慢慢聊。 大部分人可能都是通過如下的兩個途徑了解到兩粒子頂角函數:
1.單粒子格林函數求導;
2.Bethe-Salpeter方程。 其實兩者是一回事。前面我們提到過,通常我們推導關聯函數是在作用量中添加一個高斯形式的源項,然后對源項求導。這里我們要計算的是具有四費米子算符的兩粒子格林函數,所以我們需要對單粒子格林函數求源項的導數,才能構造出四費米子算符的乘積。這里,我們要稍微注意一下源項是如何進入到格林函數中的。源項的算符具有高斯型,因此會在無相互作用格林函數里出現,通過Dyson方程,也會出現在自能中。所以,單粒子格林函數對源項的求導,包含了對單粒子無相互作用格林函數部分的求導,也包含了對自能的求導。前者會給出上述圖形中前兩項,而自能對于源項的求導給出的就是頂角函數及其連續遞推公式Bethe-Salpeter方程。因為是教科書上的知識,這里我們不再做更詳細的介紹了。取決于自能中對單粒子格林函數的出現方式不同,我們會得到三個不同的Bethe-Salpeter方程,如下圖所示。這是我們通常所說的particle-hole horizontal channel、particle-hole vertical channel及particle-particle channel中的Bethe-Salpeter方程。這是我們這篇所討論內容的出發點。
在多體計算中,我們通常利用Bethe-Salpeter方程計算有頂角修正的各種極化率,圖形上對應著把上述完全頂角函數F的四個外腳兩兩連接起來,如下圖左圖所示。實際上,通過完全頂角函數我們也可以計算單粒子格林函數的自能,如下圖右圖所示。
(b)圖初看起來沒有那么熟悉,其實把完全頂角函數用其最低階近似U替代,就可以發現是我們熟悉的二階自能圖中唯一的那個相連拓撲不等價圖形。而F是包含了所有頂角相互作用的完整表示,如果我們可以嚴格計算得到F,那么通過(b)計算出的自能也將是嚴格的。通過F與自能的關系(b),原則上,我們可以構造出來一個完全自洽的理論,即通過計算兩粒子完全頂角函數,從而計算單粒子自能,再反過來通過單粒子格林函數求源項導數而計算新的完全頂角函數。 這樣的自洽過程把F與自能的關系(b)及Bethe-Salpeter方程連接在一起,形成了一個完整的同時具有單粒子和兩粒子自洽性的閉合循環。這顯然要比僅僅只有單粒子自洽性的量子多體方法要好。我們常見的格林函數微擾方法,例如Hartree-Fock、二階微擾論、fluctuation-exchange approximation (FLEX, 漲落交換近似)、non-crossing approximation(非交叉近似)等等,都是僅有單粒子層次上的自洽性。它們在兩粒子層次上不具有自洽性。 F與自能的關系(b)及Bethe-Salpeter方程都是嚴格的,如果我們可以嚴格的計算得到完全頂角函數,我們預想的同時具有兩粒子和單粒子自洽性的多體理論,自然也是一個嚴格的理論。 但是現實是我們無法嚴格而完整的計算出完全頂角函數。它是一個依賴于三個獨立動量和獨立頻率的函數,大部分情況下我們得不到它的閉合表達形式。利用數值計算,也存在實際困難。動量空間是具有周期邊條件的,但是松原頻率空間沒有周期性的,原則上所有的頻率都會貢獻自能中的內部變量求和。目前已知的所有數值計算辦法(包括量子蒙特卡洛和精確對角化)都無法得到F的全部信息。因此,我們常常不得不利用Bethe-Salpeter方程做些近似。簡單的想法是對每個channel里不可約的頂角函數Γ近似處理,然后利用Bethe-Salpeter方程迭代計算出F。因為三個channel里的F是等價的,只需要計算一個最簡單的particle-hole horizontal channel里的Bethe-Salpeter方程即可。 然而,為什么嚴格的推導會給我們三個不同channel的Bethe-Salpeter方程呢,這其中隱含了什么重要的信息嗎? 實際上這個三個Bethe-Salpeter方程并不是獨立的。當我們試圖去近似某一個Γ的時候,我們很可能就會破壞其他另外兩個channel中的Bethe-Salpeter方程。這是因為完全頂角函數F具有一個非常重要的對稱性-crossing symmetry。它連接了這三個Bethe-Salpeter方程,即通過crossing symmetry我們總是可以把其中的一個Bethe-Salpeter方程變成另外一個。當然,只有Γ是嚴格的,或者對其做了恰當的近似,才能保證這一點。很可惜,目前,我們常見的單粒子自洽理論,包括前述的Hartree-Fock、二階微擾論、fluctuation-exchange approximation (FLEX, 漲落交換近似)、non-crossing approximation(非交叉近似)等等都不滿足這一點。通過他們計算得到的兩粒子頂角函數都破壞了crossing symmetry。 什么是crossing symmetry呢?它是兩粒子頂角函數因為費米子的交換反對易性而具有的一個特性。如果我們任意交換兩個費米子算符,就會得到一個額外的負號。
兩粒子頂角函數具有和庫侖排斥力一樣的二次量子化形式,這里我們簡單的把其系數寫成算符指標的一個函數F(12;34)。在上式中我們分別交換了C2和C4兩個湮滅算符,及C2和C3一對產生湮滅算符。通過重新改寫啞元,我們得到如下的頂角函數之間的關系。
我們來形象的理解一下上面變換的意義。如果F(12;34)表示一對電子-空穴3-4散射成另外一對電子-空穴1-2,這是一個水平的散射過程,那么將C2和C4兩個湮滅算符后,就變成了從3-2散射成1-4,是一個垂直的散射過程。交換兩個算符的過程,可以形象的理解為將這兩個算符的頂角對應的外腳相互交換,這兩個外線必然要cross,所以我們把這個對稱性稱為crossing symmetry。對應于上述交換C2和C4兩個湮滅算符,crossing-symmetry將particle-hole horizontal channel中的頂角函數變到了particle-hole vertical channel中。同樣的道理,如果我們交換一個產生一個湮滅算符,比如C2和C3,我們也可以把particle-hole channel與particle-particle channel聯系起來。總而言之,費米子的交換反對稱性,使得三個channel中的Bethe-Salpeter方程并不獨立,他們之間應當可以相互轉換。 另外,因為完全頂角函數F是遵從crossing symmetry的,當我們考慮任何一個Bethe-Salpeter方程,左邊的F在crossing操作下變成了自己(符號相應的改變),等式右邊自然也應當變成自身。我們以particle-hole horizontal channel為例,等式右側的第二項,在cross c_2和c_4后會從horizontal的連接方式變成了vertical的,而不是變成自身。因此,我們只能要求等式右邊的第一項Γ中應當有一項,它能夠在cross c_2和c_4后變成等式的第二項。換句話說,Γ中應該包含vertical channel中等式右邊的第二項,它在cross 2和4后,會給出horizontal channel等式右邊的第二項。同樣的道理,Γ中也應當含有particle-particle channel中的連接方式,這樣才能保證無論怎樣交換兩個外腳,都可以保證F能夠變回自身,滿足crossing symmetry。因此,我們熟悉的Bethe-Salpeter方程中的Γ應該表示成如下的樣子:
這里將在每一個channel中不可約(不可約的意思是說,不能夠通過剪斷任意兩條內部的格林函數線使其分成兩個獨立的部分)的Γ進一步分解,其中Λ被稱為完全不可約頂角函數,它在三個channel中都是一樣的,并且在任何一個channel中都是兩粒子不可約的。作為對比,這里我們強調一下,Γ_ph僅在particle-hole horizontal channel里是不可約的,我們不能再進一步通過剪斷兩條單粒子格林函數線把它分解成horizontal方向上的兩個獨立部分了。但是Γ_ph在其他channel就變成可約的了。比如在particle-hole vertical channel里,我們要剪斷垂直的兩個格林函數線。按照上圖,這顯然是可以把Γ_ph等式右側的第二張圖分成兩部分。所以我們說,Γ_ph在vertical channel里可約的。同樣的道理,Γ_ph在paritlce-particle channel里也是可約的。 上圖對于Γ的分解,構成了一組新的方程,我們稱之為parquet方程。這樣的分解完全保證了兩粒子完全頂角函數F具有crossing symmetry。這時候,我們就可以安全的對Λ做近似,而不會破壞crossing symmetry了。這顯然比在Bethe-Salpeter方程中對三個Γ做近似要更有優越性。對于如何求解完整的parquet 方程,可以參考筆者的程序和方法 [1, 2]。 我們可以把Λ用它的最低階近似U來替代,叫做parquet approximation。2007年,K. Held組用動力學平均場方法嚴格計算了局域完全不可約頂角函數Λ, 并用動力學平均場lattice格林函數來替換parquet方程中的格林函數線。這樣做,完全不可約頂角函數雖然是局域的,但是通過parquet方程及Bethe-Salpeter方程,我們可以計算得到非局域的完全頂角函數F,從而計算得到非局域的自能。因此,這也構成了一種動力學平均場的非局域擴展方法,稱之為dynamical vertex approximation [3]. 這里我們不再進一步闡述這個方法了,剩下的大部分都是數值計算的細節了。通過和Dual Fermion及non-local expansion方法對比,我們可以看到,雖然這些方法的出發點不同,但是自能的非局域修正均來自于局域兩粒子頂角函數的非局域連接。任何單粒子層次上的非局域性,都無法進入到自能中,都僅僅只是在由impurity格林函數變換成lattice格林函數的過程中起作用。自能,作為單粒子中的相互作用部分,其本質是來自于兩體相互作用,因此任何非局域的修正來至于兩粒子頂角函數也是情理之中。基于這樣的思想,也可以通過局域兩粒子頂角函數的不同連接方式,構造出全新的量子多體方法,對動力學平均場的局域自能進行非局域修正。這是一個嶄新的領域,雖然略有門檻,但是有很多可以嘗試和擴展的東西。目前的非局域擴展多集中在單軌道體系中,Hubbard相互作用,如何將非局域擴展方法更為核心的部分抽出來,簡化計算,使得它更好的適用于真實材料體系的研究,將會是下一個研究中心。
結束的話
《動力學平均場-三十而已》這個系列,算上前言,一共9篇,到這里就告一段落了,感謝各位讀者每期的陪伴。國內做動力學平均場方法論的同行不多,我最初的目的僅僅只是自說自話,簡單的科普一下,同時給自己的學生寫一個簡單的學習綱要。語言上有意在往輕松詼諧的方向上靠攏,每期想得更多的是如何把復雜的問題講的更有趣、更容易聯想記憶。隨著慢慢寫開來,意外的收到了很多反饋和鼓勵,這才讓我意識到,原來我以為的這些枯燥無趣的量子多體方法,其實有很多朋友在關注。因此,后期的文章少了些風趣,多了些嚴謹;缺少了科普性,更像是lecture note了。如果有讀者在熱鬧之余,還能從這個系列中總結出自己學習量子多體方法的路線、能對多個不同小方向上的知識點融會貫通,我想這個系列的任務就算超額完成了。 動力學平均場走過三十年的發展歷程,回頭看,其實是量子多體方法論在嚴謹性和可行性之間不斷嘗試、取舍的過程。動力學平均場抓住了量子多體問題的一個核心,即大多數情況下動力學漲落要大于空間漲落。動力學平均場的發展使得強關聯電子材料的計算更為準確,讓我們多了一套普適性更廣的量子多體方法。我相信,在各位年輕讀者的努力下,動力學平均場還會有下一個三十年,還將取得更好的發展。一方面因為它在材料計算上體現出了非凡的活力,另一方面也是因為它仍然有這么多不完美的地方,才更值得我們去尋找更好的動力學平均場理論。這需要理論工作者的努力,更需要諸如數學物理、計算機技術、計算物理上的進步。正因為這樣,年輕的朋友們才更有施展才華的空間。我也很期待,一個能同時描述空間和時間漲落、刻畫任意多體關聯、適用于多軌道真實體系的更好理論的出現。
責任編輯:lq
-
函數
+關注
關注
3文章
4332瀏覽量
62653 -
方程
+關注
關注
0文章
33瀏覽量
16934
原文標題:【知社特刊】動力學平均場 | 最終章:超越局域近似—費曼圖展開(2)
文章出處:【微信號:zhishexueshuquan,微信公眾號:知社學術圈】歡迎添加關注!文章轉載請注明出處。
發布評論請先 登錄
相關推薦
磁調制式電流傳感器在粒子加速器中的應用
SUMIF函數與SUMIFS函數的區別
熱解粒子探測器與什么相似
熱解粒子式電氣火災監控探測器原理
熱解粒子探測器干嘛用的
臺式塵埃粒子計數器的功能優勢與應用
邏輯函數的化簡方法有哪兩種
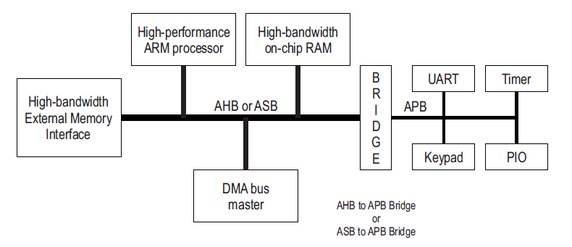
聊聊AMBA協議的evolution過程




 聊聊兩粒子頂角函數的有趣之處
聊聊兩粒子頂角函數的有趣之處












評論