量子力學曾是一門富有爭議的學說。早期的批判者（如愛因斯坦）曾在量子力學領域留下一句名言，即“上帝不會擲骰子”（指的是量子測量的概率特性），尼爾斯·玻爾對此評論道：“愛因斯坦，不要對上帝指手畫腳。”然而大家都同意愛因斯坦的觀點，引用約翰·惠勒的一句話就是，“如果你不曾為量子力學困惑不已，則將無法領略其中的真諦”。

隨著對量子力學的認識不斷深入，我們不僅從中收獲到許多重要的物理發(fā)現(xiàn)，同時也通過量子力學催生了量子計算領域。量子計算是一門與傳統(tǒng)計算不同的計算范式。此領域以量子力學原理為基礎，并不斷加以開發(fā)，從而可獲得比使用傳統(tǒng)計算機更快的速度（在某些情況下可實現(xiàn)超多項式時間）。

在這篇文章中，我會聊聊自己在開始研究量子機器學習 (QML) 時面臨到的一些挑戰(zhàn)，以及我通過 TensowFlow Quantum(TFQ) 和 Cirq 受益并幫助其他研究人員探索量子計算和 QML 領域的方法。因為我之前接觸過 TensorFlow，所以使用 TensorFlow Quantum 對我來說也是輕車熟路。事實證明，TFQ 對我完成工作很有幫助，然后終于在第 16 屆 AIIDE 會議上，我在量子強化學習領域用 TFQ 發(fā)表了我的首個作品，而那則是我最輝煌的時刻。我希望這篇文章可以幫助和激勵其他研究人員、新手和專家，使其通過 TFQ 進一步推動 QML 領域的發(fā)展。

QML 背景

QML 和機器學習在傳統(tǒng)神經(jīng)網(wǎng)絡/深度學習方法方面有著重要的相似性和不同點。這兩種方法均可看做是使用了轉(zhuǎn)換的“堆疊層”，而這正是較大模型的構(gòu)成要素。在這兩種情況下，我們通常會為了最小化某些損失函數(shù)，將數(shù)據(jù)用于通知模型參數(shù)更新（大多情況下是這樣，但不完全都是通過基于梯度的方法）。這兩種方法的不同之處在于，QML 模型可以利用量子力學的力量，而深度神經(jīng)網(wǎng)絡則不能。我們會將一種由 TFQ 提供技術(shù)支持的重要 QML 稱作變分量子電路 (QVC)。QVC 也可稱作量子神經(jīng)網(wǎng)絡 (QNN)。

QVC 如下圖所示（來自 TFQ 白皮書）。圖表閱讀順序為從左往右，其中量子位由水平橫線表示。QVC 可分為三個重要而又不同的部分：編碼器電路、變分電路和測量運算符。編碼器電路可以接收自然量子數(shù)據(jù)（如非參數(shù)化量子電路），或?qū)鹘y(tǒng)數(shù)據(jù)轉(zhuǎn)化為量子數(shù)據(jù)。編碼器電路連接到變分電路，后者由其可學習參數(shù)定義。在學習過程中更新的部分即為電路的參數(shù)化部分。QVC 最后的組成部分為測量運算符。如要從 QVC 中提取信息，必須應用某種量子測量方法（如 Pauli X、Y 或 Z 基的測量）。通過使用提取自這些測量方法中的信息，我們得以在傳統(tǒng)計算機上計算損失函數(shù)（以及梯度）并更新參數(shù)。同時，可通過類似傳統(tǒng)神經(jīng)網(wǎng)絡（如 Adam 或 RMSProp）的優(yōu)化器來優(yōu)化這些梯度。QVC 也可與傳統(tǒng)神經(jīng)網(wǎng)絡相結(jié)合（如圖所示），因為量子電路具備可微分性，因此梯度可以反向進行傳播。

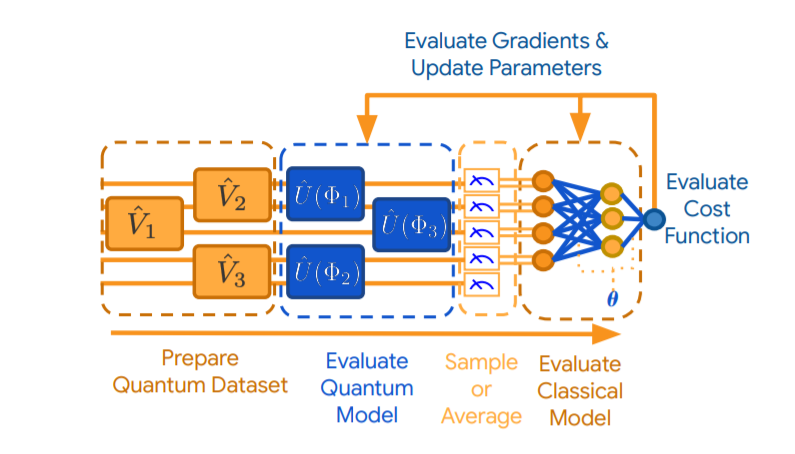
TFQ 白皮書
https://arxiv.org/abs/2003.02989

然而圍繞 QVC 的直觀模型和數(shù)學框架與傳統(tǒng)神經(jīng)網(wǎng)絡有一些重要區(qū)別，而在這些差異中存在著量子加速的潛能。量子計算和 QML 可以對量子現(xiàn)象加以利用，如疊加和糾纏。疊加源自于波函數(shù)，而波函數(shù)是多個狀態(tài)的線性組合，可讓量子位同時呈現(xiàn)出兩種不同的狀態(tài)（以概率的方式）。能夠在此類疊加上采取操作（即同時對多個狀態(tài)進行操作）是量子力學計算不可或缺的一部分。糾纏是一種通過多量子位門生成的復雜現(xiàn)象。對這些概念和量子計算具有基本的了解是使用 QML 的重要前提。這里有關于上述內(nèi)容的大量可用資源，如 Preskill 的量子計算課程和 de Wolf 的講義。

Preskill 的量子計算課程
http://theory.caltech.edu/~preskill/ph219/ph219_2018-19

de Wolf 的講義
https://arxiv.org/pdf/1907.09415.pdf

不過目前想要使用真正的量子硬件，條件極為有限，因此很多量子計算研究人員都在模擬的量子計算機上進行工作。近期和當前的量子設備都具備 10 到 100 個量子位 (qubit)，如 Google Sycamore 處理器。因其外觀尺寸和產(chǎn)生的噪音，這種硬件通常又被稱為嘈雜中型量子 (NISQ) 技術(shù)。TFQ 和 Cirq 即是為這些近期的 NISQ 設備量身打造而成。鑒于當前的糾錯技術(shù)，這些設備要比某些通過著名量子算法實現(xiàn)量子加速的設備小得多；例如，秀爾算法需要上千個量子位，而量子近似優(yōu)化算法 (QAOA) 可能至少需要 420 個量子位才能獲得量子優(yōu)勢。然而 NISQ 設備在實現(xiàn)量子加速方面仍有巨大潛能（如 Google 通過 53 個量子位進行驗證地那樣）。

Google Sycamore 處理器
https://ai.googleblog.com/2019/10/quantum-supremacy-using-programmable.html

TFQ 和我的工作

TFQ 于今年（2020 年）3 月中旬發(fā)布，發(fā)布后不久我便開始使用。自那時起，我就已開始研究 QML，并格外關注了用于強化學習 (RL) 的 QML。盡管我已經(jīng)在量子電路模擬器的無障礙功能方面取得了巨大進步，但是仍然很難踏入 QML 這一領域。除了在數(shù)學和物理方面遇到的困難，根本困難則是位實現(xiàn)成果所投入的時間。對于那些從事傳統(tǒng)機器學習的研究人員來說，從頭開始編寫 QVC 所需的時間，以及正確測試和調(diào)試 QVC 花費的時間（更不用說優(yōu)化）都是一種挑戰(zhàn)。花費大量時間去構(gòu)建一個可能會失敗的試驗品，對我來說風險巨大，尤其我當時還是一個即將畢業(yè)的大學生！幸運的是，我不用冒這個險。隨著 TFQ 的發(fā)布，我可以在其中輕松即時地將我的想法轉(zhuǎn)變?yōu)楝F(xiàn)實。實際上，如果 TFQ 不曾發(fā)布，那我可能永遠也無法完成這項工作。受先前工作的啟發(fā)，我們擴展性地在 RL 任務中應用了 QML。

強化學習
http://www.incompleteideas.net/book/RLbook2020.pdf

先前工作
https://ieeexplore.ieee.org/abstract/document/9144562

通過這一做法，我們證明了在當代 RL 算法中使用 QVC 代替神經(jīng)網(wǎng)絡的潛力（特別是 DQN 和 DDQN）。同時我們也展示了使用多類 QVC 模型的潛力，通過使用具有密集層或量子池層（分別表示混合動力和純動力）的 QVC 來減少正確輸出空間中量子位的數(shù)量。

DQN
https://www.cs.toronto.edu/~vmnih/docs/dqn.pdf

DDQN
https://arxiv.org/pdf/1509.06461.pdf

量子池層
https://arxiv.org/abs/1810.03787

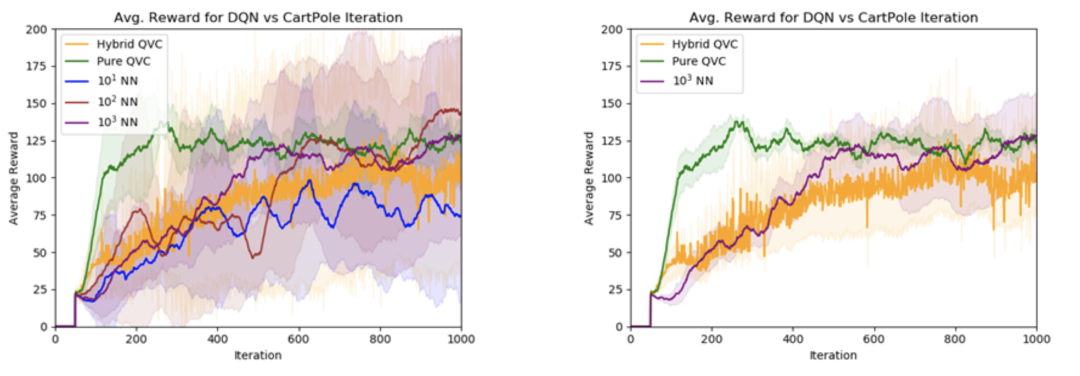
QVC 所具有的代表性效力也得以呈現(xiàn)；通過使用具備約 50 個參數(shù)的 QVC，我們能夠收獲等同于在神經(jīng)網(wǎng)絡上使用更多數(shù)量級參數(shù)所呈現(xiàn)的性能。從圖上我們可以對比得出，在典型 CartPole 環(huán)境（讓小車上的一個倒立擺保持平衡）中達成的性能，左圖包括所有的神經(jīng)網(wǎng)絡，而右圖只顯示了最大的神經(jīng)網(wǎng)絡。NN 前面的數(shù)字代表參數(shù)空間的大小。

我們會繼續(xù)在 RL 中應用 QML，并為大家呈現(xiàn)更多稿件。這項工作現(xiàn)已納入 2020 NeurIPS 研討會：“預注冊實驗：用于機器學習研究的可替換發(fā)布模型?！?/p>

TFQ 使用建議

無論您的背景如何，只要您對 QML 研究感興趣，那 TFQ 對您來說都將是一個極佳的工具。在科學界，擁有“發(fā)表或者滅亡”的心態(tài)早已習以為常，不過這可能會扼殺創(chuàng)新工作并抑制思維的發(fā)散，對于那些需要采取大量實操工作的實驗而言更是如此。TFQ 不僅可以幫助您加速實驗，還可以助您輕松實現(xiàn)那些可能永遠難以試驗的想法。付諸實踐是實現(xiàn)很多新鮮有趣想法的常見阻礙，到目前為止由于將想法轉(zhuǎn)化為現(xiàn)實異常困難，很多想法依然停留在構(gòu)想階段，而 TFQ 則可以輕松做到這一點。

扼殺創(chuàng)新工作
https://www.theguardian.com/science/2013/dec/06/peter-higgs-boson-academic-system

對于初學者而言，TFQ 是出色的入門工具，即使您沒有大量的時間來研究編碼，您依然能從中收獲大量知識。無需從頭開始構(gòu)建，即可借助 QVC 進行嘗試和實驗。不得不說，這的確是一款令人難以置信的工具。對于有 TensorFlow 使用經(jīng)驗的傳統(tǒng) ML 研究人員來說，其可通過 TFQ，輕松完成對 QML 的小規(guī)?；虼笠?guī)模的過渡和轉(zhuǎn)換。TFQ 的 API 和其提供的模塊（如 Keras-esque 層和微分器）與 TF 的設計原則一致，而這一相似性則更有利于輕松完成編程轉(zhuǎn)換。對于身處 QML 領域的研究人員來說，TFQ 當然也能有所助力。

大規(guī)模
https://arxiv.org/abs/2011.01938

如想上手使用 TFQ，則必須要熟悉量子計算的基礎知識。您可以參閱上述參考資料或是除此之外的其他資源。還有另一個經(jīng)常遭到忽視的重要步驟，那就是閱讀 TFQ 白皮書。白皮書可供 QML 初學者使用，其中介紹了大量有關 QML 的理論知識，以及 TFQ 的基礎和高級用法。閱讀白皮書和使用 TFQ 同樣重要。試著嘗試不同的事物，如實驗；通過開展實驗，您不僅可以進一步了解軟件，還可以加深對理論和數(shù)學的理解。通過閱讀其他當代論文及引用了 TFQ 的論文，亦可讓自己沉浸于該領域正在進行的研究之中。

責任編輯：lq