本文采用圖像展示的方式幫助大家理解相關(guān)復(fù)雜的數(shù)學(xué)方程。聚焦于理解神經(jīng)網(wǎng)路如何工作,主要關(guān)注于CNNs的一些典型問題:數(shù)字圖像的數(shù)據(jù)結(jié)構(gòu)、步幅卷積、連接剪枝和參數(shù)共享、卷積層反向傳播、池化層等。
原標(biāo)題:Gentle Dive into Math Behind Convolutional Neural Networks
自動駕駛、智能醫(yī)療保健和自助零售這些領(lǐng)域直到最近還被認(rèn)為是不可能實現(xiàn)的,而計算機視覺已經(jīng)幫助我們達到了這些事情。如今,擁有自動駕駛汽車或自動雜貨店的夢想聽起來不再那么遙不可及了。事實上,我們每天都在使用計算機視覺——當(dāng)我們用面部解鎖手機或在社交媒體上發(fā)照片前使用自動修圖。卷積神經(jīng)網(wǎng)絡(luò)可能是這一巨大成功背后最關(guān)鍵的構(gòu)建模塊。這一次,我們將加深理解神經(jīng)網(wǎng)絡(luò)如何工作于CNNs。出于建議,這篇文章將包括相當(dāng)復(fù)雜的數(shù)學(xué)方程,如果你不習(xí)慣線性代數(shù)和微分,請不要氣餒。我的目標(biāo)不是讓你們記住這些公式,而是讓你們對下面發(fā)生的事情有一個直觀的認(rèn)識。
附注:在這篇文章中,我主要關(guān)注CNNs的一些典型問題。如果您正在尋找關(guān)于深度神經(jīng)網(wǎng)絡(luò)更基礎(chǔ)的信息,我建議您閱讀我在本系列文章中的其他文章(https://towardsdatascience.com/https-medium-com-piotr-skalski92-deep-dive-into-deep-networks-math-17660bc376ba)。與往常一樣,可以在我的GitHub上找到帶有可視化和注釋的完整源代碼,讓我們開始吧!
介紹
過去我們已經(jīng)知道被稱為緊密連接的神經(jīng)網(wǎng)絡(luò)。這些網(wǎng)絡(luò)的神經(jīng)元被分成若干組,形成連續(xù)的層。每一個這樣的神經(jīng)元都與相鄰層的每一個神經(jīng)元相連。下圖顯示了這種體系結(jié)構(gòu)的一個示例。
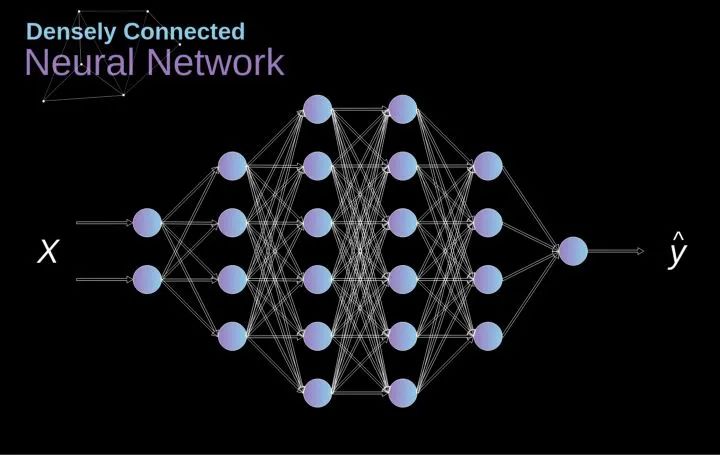
圖1. 密集連接的神經(jīng)網(wǎng)絡(luò)結(jié)構(gòu)
當(dāng)我們根據(jù)一組有限的人工設(shè)計的特征來解決分類問題時,這種方法很有效。例如,我們根據(jù)足球運動員在比賽期間的統(tǒng)計數(shù)據(jù)來預(yù)測他的位置。然而,當(dāng)處理照片時,情況變得更加復(fù)雜。當(dāng)然,我們可以將每個像素的像素值作為單獨的特征,并將其作為輸入傳遞給我們的密集網(wǎng)絡(luò)。不幸的是,為了讓該網(wǎng)絡(luò)適用于一張?zhí)囟ǖ?a href="http://m.1cnz.cn/v/tag/11230/" target="_blank">智能手機照片,我們的網(wǎng)絡(luò)必須包含數(shù)千萬甚至數(shù)億個神經(jīng)元。另一方面,我們可以縮小我們的照片,但在這個過程中,我們會丟失一些有用的信息。我們立馬意識到傳統(tǒng)的策略對我們沒有任何作用,我們需要一個新的有效的方法,以充分利用盡可能多的數(shù)據(jù),但同時減少必要的計算和參數(shù)量。這就是CNNs發(fā)揮作用的時候了。
數(shù)字圖像的數(shù)據(jù)結(jié)構(gòu)
讓我們先花一些時間來解釋數(shù)字圖像是如何存儲的。你們大多數(shù)人可能知道它們實際上是由很多數(shù)字組成的矩陣。每一個這樣的數(shù)字對應(yīng)一個像素的亮度。在RGB模型中,彩色圖像實際上是由三個對應(yīng)于紅、綠、藍三種顏色通道的矩陣組成的。在黑白圖像中,我們只需要一個矩陣。每個矩陣都存儲0到255之間的值。這個范圍是存儲圖像信息的效率(256之內(nèi)的值正好可以用一個字節(jié)表達)和人眼的敏感度(我們區(qū)分有限數(shù)量的相同顏色灰度值)之間的折衷。
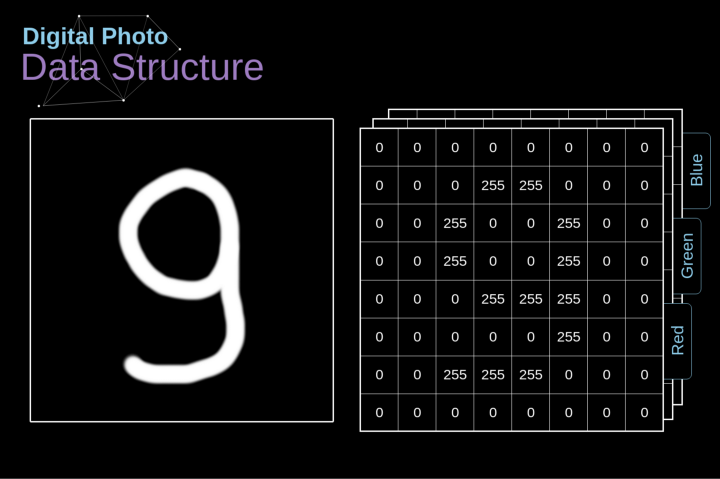
圖2. 數(shù)字圖像的數(shù)據(jù)結(jié)構(gòu)
卷積
核卷積不僅用于神經(jīng)網(wǎng)絡(luò),而且是許多其他計算機視覺算法的關(guān)鍵一環(huán)。在這個過程中,我們采用一個形狀較小的矩陣(稱為核或濾波器),我們輸入圖像,并根據(jù)濾波器的值變換圖像。后續(xù)的特征map值根據(jù)下式來計算,其中輸入圖像用f表示,我們的kernel用h表示,結(jié)果矩陣的行和列的索引分別用m和n表示。
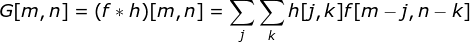 圖片
圖片
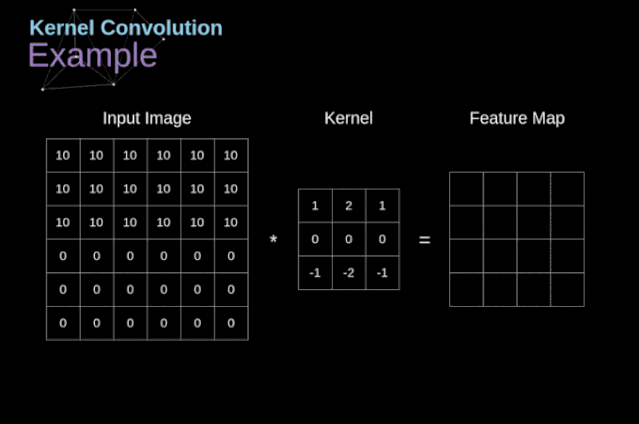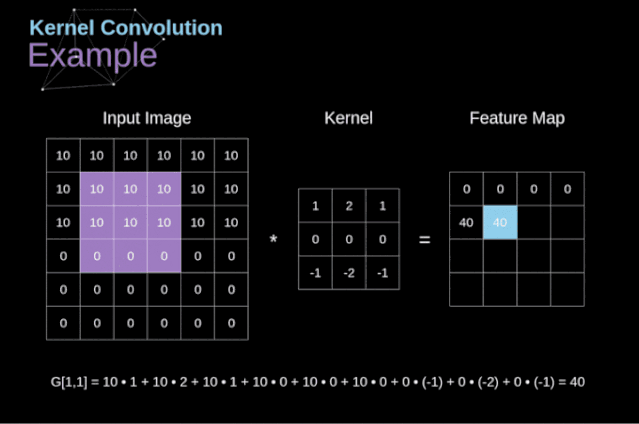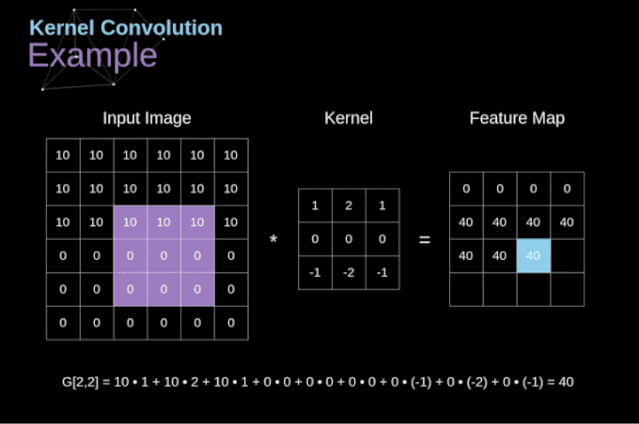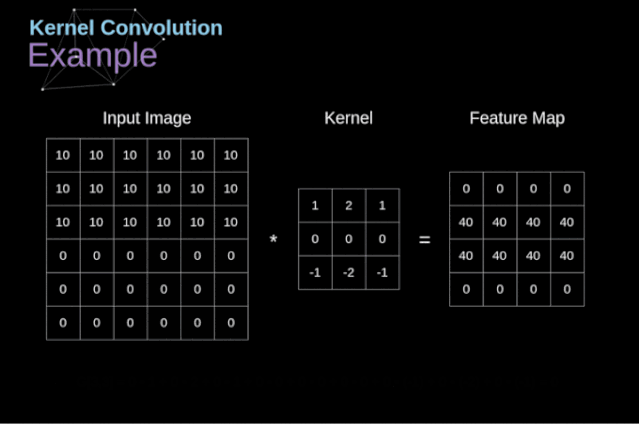
圖3. 核卷積的例子
將過濾器放置在選定的像素上之后,我們從kernel中提取每個相應(yīng)位置的值,并將它們與圖像中相應(yīng)的值成對相乘。最后,我們總結(jié)了所有內(nèi)容,并將結(jié)果放在輸出特性圖的對應(yīng)位置。上面我們可以看到這樣的操作在細節(jié)上是怎么實現(xiàn)的,但是更讓人關(guān)注的是,我們通過在一個完整的圖像上執(zhí)行核卷積可以實現(xiàn)什么應(yīng)用。圖4顯示了幾種不同濾波器的卷積結(jié)果。

圖4. 通過核卷積得到邊緣[原圖像:https://www.maxpixel.net/Idstein-Historic-Center-Truss-Facade-Germany-3748512]
有效卷積和相同卷積
如圖3所示,當(dāng)我們用3x3核對6x6的圖像進行卷積時,我們得到了4x4特征圖。這是因為只有16個不同的位置可以讓我們把濾波器放在這個圖片里。因為每次卷積操作,圖像都會縮小,所以我們只能做有限次數(shù)的卷積,直到圖像完全消失。更重要的是,如果我們觀察卷積核如何在圖像中移動,我們會發(fā)現(xiàn)位于圖像邊緣的像素的影響要比位于圖像中心的像素小得多。這樣我們就丟失了圖片中包含的一些信息。通過下圖,您可以知道像素的位置如何改變其對特征圖的影響。
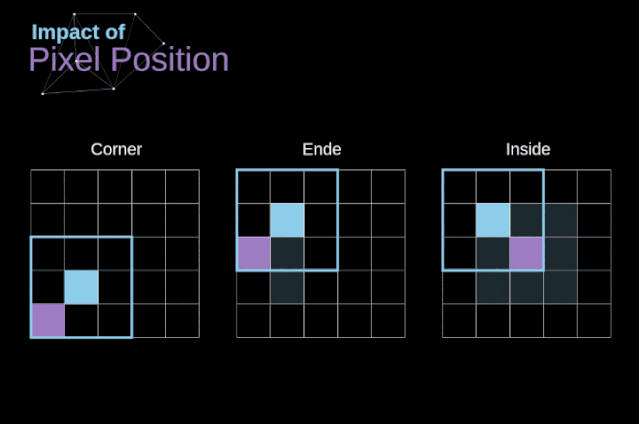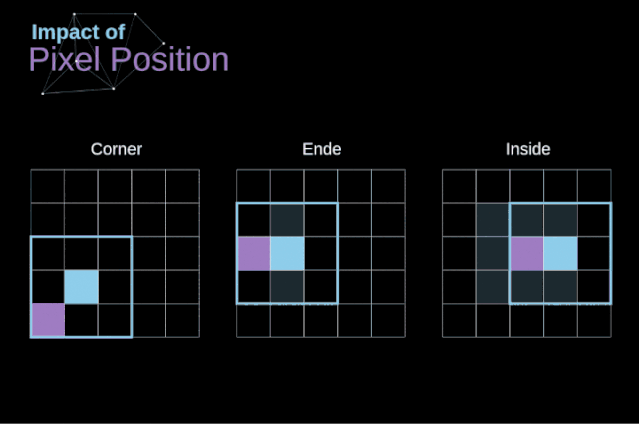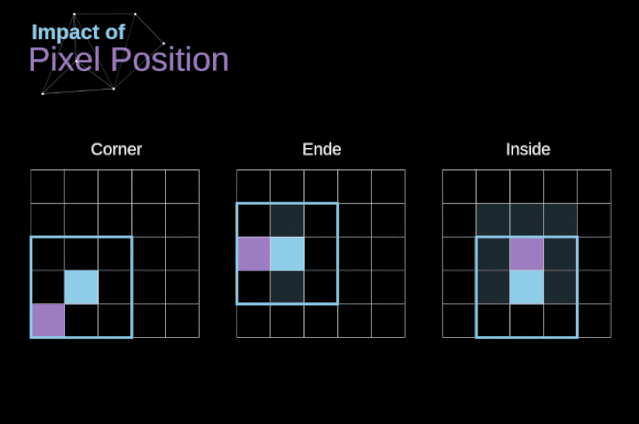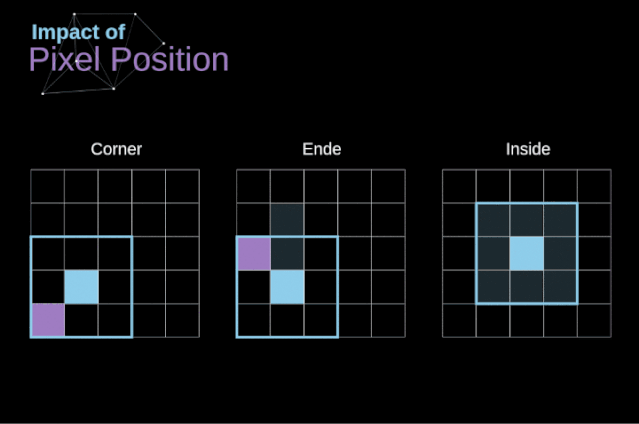
圖5. 像素位置的影響
為了解決這兩個問題,我們可以用額外的邊框填充圖像。例如,如果我們使用1px填充,我們將照片的大小增加到8x8,那么與3x3濾波器卷積的輸出將是6x6。在實踐中,我們一般用0填充額外的填充區(qū)域。這取決于我們是否使用填充,我們要根據(jù)兩種卷積來判斷-有效卷積和相同卷積。這樣命名并不是很合適,所以為了清晰起見:Valid表示我們僅使用原始圖像,Same表示我們同時也考慮原圖像的周圍邊框,這樣輸入和輸出的圖像大小是相同的。在第二種情況下,填充寬度應(yīng)該滿足以下方程,其中p為填充寬度和f是濾波器維度(一般為奇數(shù))。
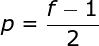
步幅卷積
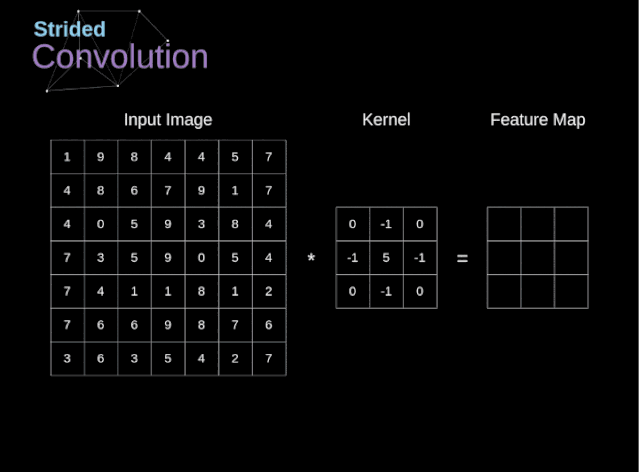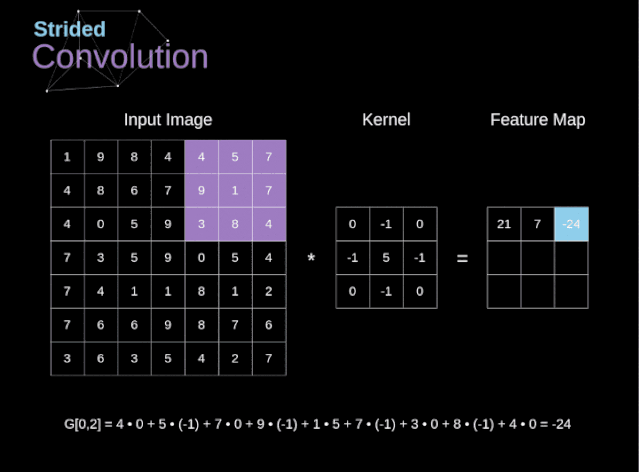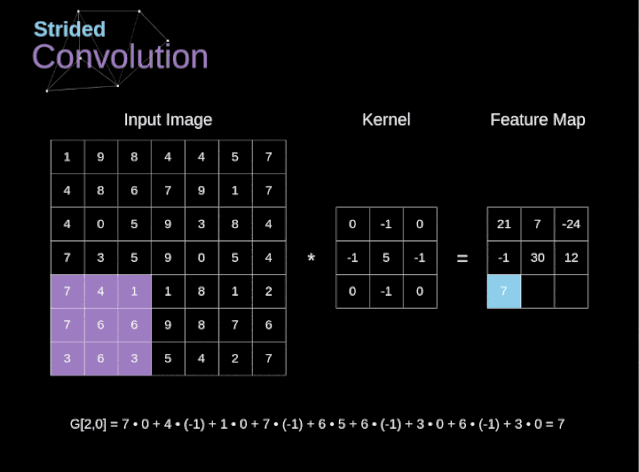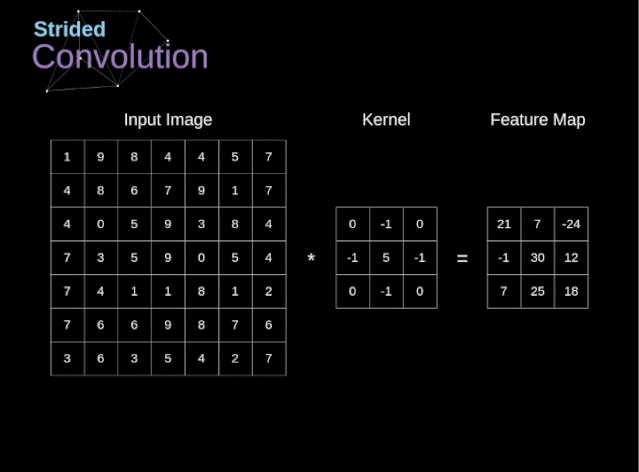
圖6. 步幅卷積的例子
在前面的例子中,我們總是將卷積核每次移動一個像素。但是,步幅也可以看作卷積層超參數(shù)之一。在圖6中,我們可以看到,如果我們使用更大的步幅,卷積看起來是什么樣的。在設(shè)計CNN架構(gòu)時,如果希望感知區(qū)域的重疊更少,或者希望feature map的空間維度更小,我們可以決定增加步幅。輸出矩陣的尺寸——考慮到填充寬度和步幅——可以使用以下公式計算。
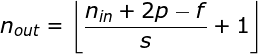
過渡到三維
空間卷積是一個非常重要的概念,它不僅能讓我們處理彩色圖像,更重要的是在單層中應(yīng)用多個卷積核。第一個重要的原則是,過濾器和要應(yīng)用它的圖像必須具有相同通道數(shù)。基本上,這種方式與圖3中的示例非常相似,不過這次我們將三維空間中的值與卷積核對應(yīng)相乘。如果我們想在同一幅圖像上使用多個濾波器,我們分別對它們進行卷積,將結(jié)果一個疊在一起,并將它們組合成一個整體。接收張量的維數(shù)(即我們的三維矩陣)滿足如下方程:n-圖像大小,f-濾波器大小,nc-圖像中通道數(shù),p-是否使用填充,s-使用的步幅,nf-濾波器個數(shù)。
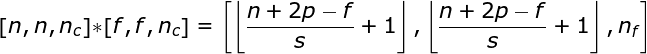
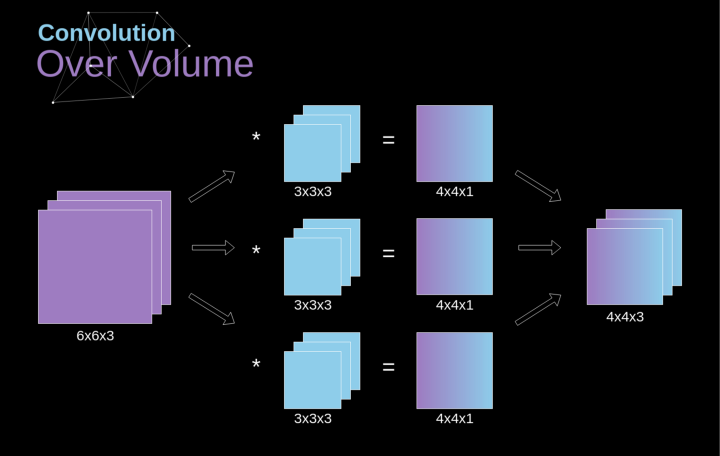
圖7. 三維卷積
卷積層
現(xiàn)在是時候運用我們今天所學(xué)的知識來構(gòu)建我們的CNN層了。我們的方法和我們在密集連接的神經(jīng)網(wǎng)絡(luò)中使用的方法幾乎是一樣的,唯一的不同是這次我們將使用卷積而不是簡單的矩陣乘法。正向傳播包括兩個步驟。第一步是計算中間值Z,這是利用輸入數(shù)據(jù)和上一層權(quán)重W張量(包括所有濾波器)獲得的卷積的結(jié)果,然后加上偏置b。第二步是將非線性激活函數(shù)的應(yīng)用到獲得的中間值上(我們的激活函數(shù)表示為g)。對矩陣方程感興趣的讀者可以在下面找到對應(yīng)的數(shù)學(xué)公式。如果您不清楚其中的操作細節(jié),我強烈推薦我的前一篇文章,在那篇文章中,我詳細討論了緊密連接的神經(jīng)網(wǎng)絡(luò)的原理。順便說一下,在下圖中你可以看到一個簡單的可視化,描述了方程中使用的張量的維數(shù)。
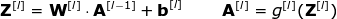
圖8.張量維度
連接剪枝和參數(shù)共享
在文章的開頭,我提到密集連接的神經(jīng)網(wǎng)絡(luò)不擅長處理圖像,這是因為需要學(xué)習(xí)大量的參數(shù)。既然我們已經(jīng)理解了卷積是什么,讓我們現(xiàn)在考慮一下它是如何優(yōu)化計算的。在下面的圖中,以稍微不同的方式顯示了二維卷積,以數(shù)字1-9標(biāo)記的神經(jīng)元組成了輸入層,并接受圖像像素亮度值,而A - D單元表示計算出的特征map元素。最后,I-IV是需要經(jīng)過學(xué)習(xí)的卷積核的值。
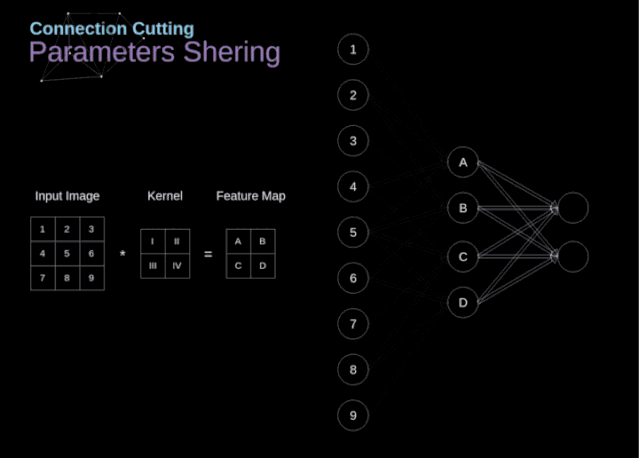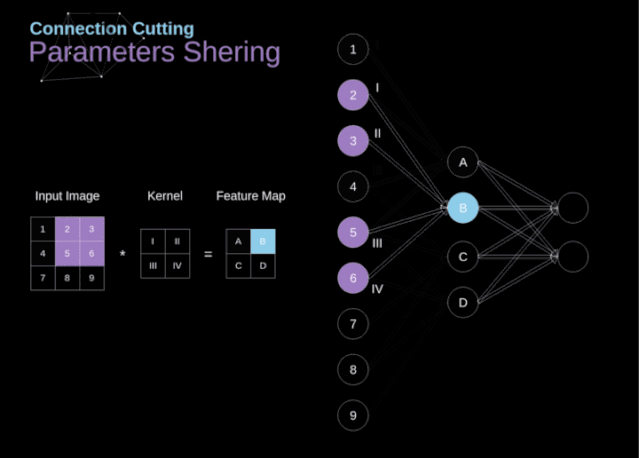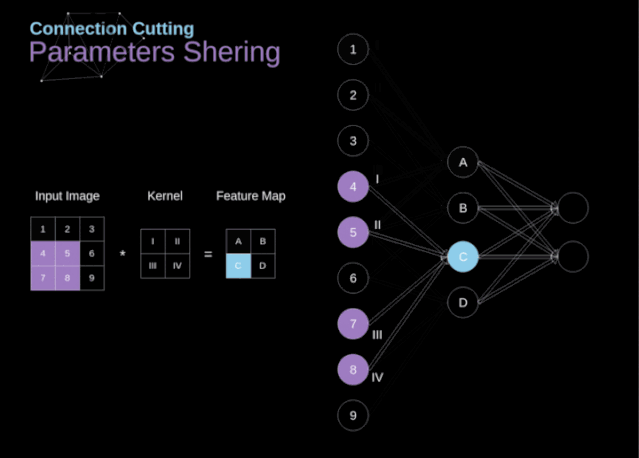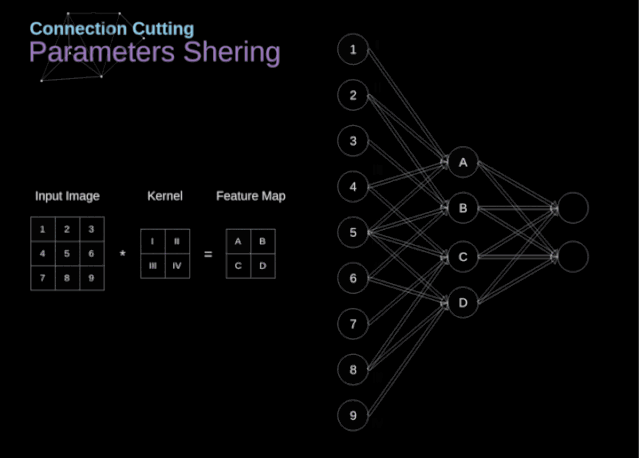
圖9. 連接剪枝和參數(shù)共享
現(xiàn)在,讓我們關(guān)注卷積層的兩個非常重要的屬性。首先,你可以看到,并不是所有連續(xù)兩層的神經(jīng)元都相互連接。例如,神經(jīng)元1只影響A的值。其次,我們看到一些神經(jīng)元共享相同的權(quán)重。這兩個性質(zhì)都意味著我們需要學(xué)習(xí)的參數(shù)要少得多。順便說一下,值得注意的是,濾波器中的一個值會影響特征map中的每個元素——這在反向傳播過程中非常重要。
卷積層反向傳播
任何嘗試過從頭編寫自己的神經(jīng)網(wǎng)絡(luò)代碼的人都知道,完成正向傳播還沒有完成整個算法流程的一半。真正的樂趣在于你想要進行反向傳播得到時候。現(xiàn)在,我們不需要為反向傳播這個問題所困擾,我們可以利用深度學(xué)習(xí)框架來實現(xiàn)這一部分,但是我覺得了解底層是有價值的。就像在密集連接的神經(jīng)網(wǎng)絡(luò)中,我們的目標(biāo)是計算導(dǎo)數(shù),然后用它們來更新我們的參數(shù)值,這個過程叫做梯度下降。
在我們的計算中需要用到鏈?zhǔn)椒▌t——我在前面的文章中提到過。我們想評估參數(shù)的變化對最終特征map的影響,以及之后對最終結(jié)果的影響。在我們開始討論細節(jié)之前,讓我們就對使用的數(shù)學(xué)符號進行統(tǒng)一——為了讓過程更加簡化,我將放棄偏導(dǎo)的完整符號,而使用如下所示的更簡短的符號來表達。但記住,當(dāng)我用這個符號時,我總是指的是損失函數(shù)的偏導(dǎo)數(shù)。
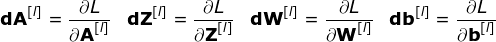
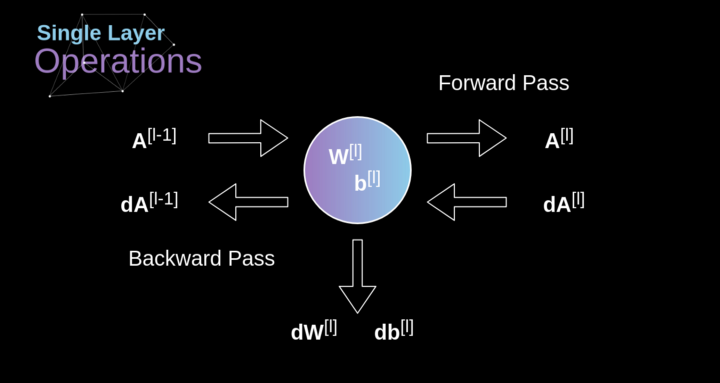
圖10. 單卷積層的輸入和輸出的正向和反向傳播
我們的任務(wù)是計算dW[l]和db[l]——它們是與當(dāng)前層參數(shù)相關(guān)的導(dǎo)數(shù),以及dA[l -1]的值——它們將被傳遞到上一層。如圖10所示,我們接收dA[l]作為輸入。當(dāng)然,張量dW和W、db和b以及dA和A的維數(shù)是相同的。第一步是通過對輸入張量的激活函數(shù)求導(dǎo)得到中間值dZ[l]。根據(jù)鏈?zhǔn)椒▌t,后面將使用這個操作得到的結(jié)果。
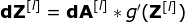
現(xiàn)在,我們需要處理卷積本身的反向傳播,為了實現(xiàn)這個目的,我們將使用一個矩陣運算,稱為全卷積,如下圖所示。注意,在這個過程中,對于我們使用卷積核,之前我們將其旋轉(zhuǎn)了180度。這個操作可以用下面的公式來描述,其中濾波器用W表示,dZ[m,n]是一個標(biāo)量,屬于上一層偏導(dǎo)數(shù)。
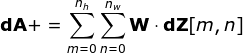
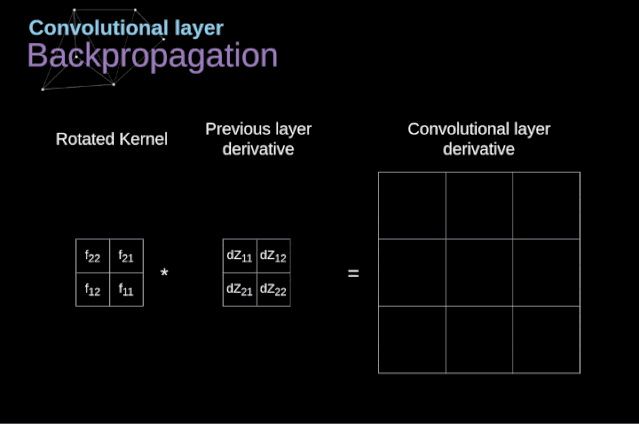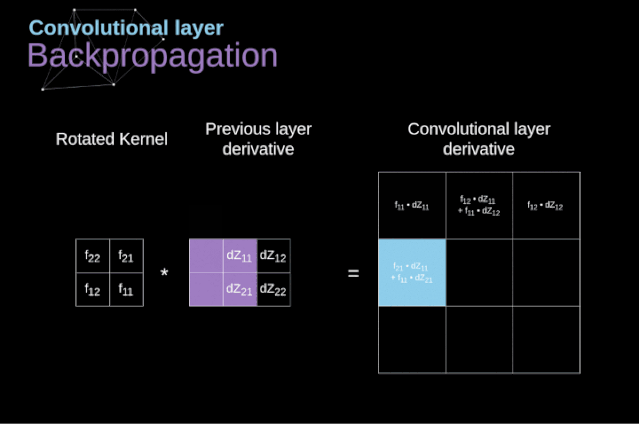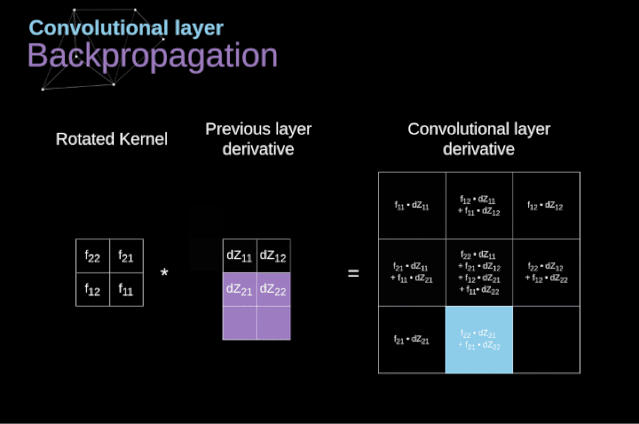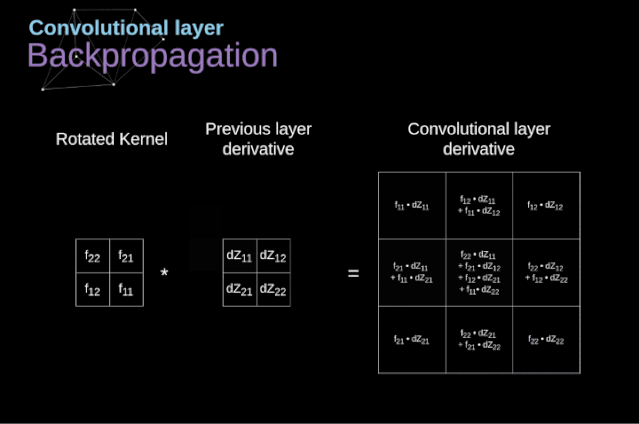
圖11. 全卷積
池化層
除了卷積層,CNNs還經(jīng)常使用所謂的池化層。池化層主要用于減小張量的大小和加速計算。這種網(wǎng)絡(luò)層很簡單——我們需要將圖像分割成不同的區(qū)域,然后對每個部分執(zhí)行一些操作。例如,對于最大值池化層,我們從每個區(qū)域中選擇一個最大值,并將其放在輸出中相應(yīng)的位置。在卷積層的情況下,我們有兩個超參數(shù)——濾波器大小和步長。最后一個比較重要的一點是,如果要為多通道圖像進行池化操作,則應(yīng)該分別對每個通道進行池化。
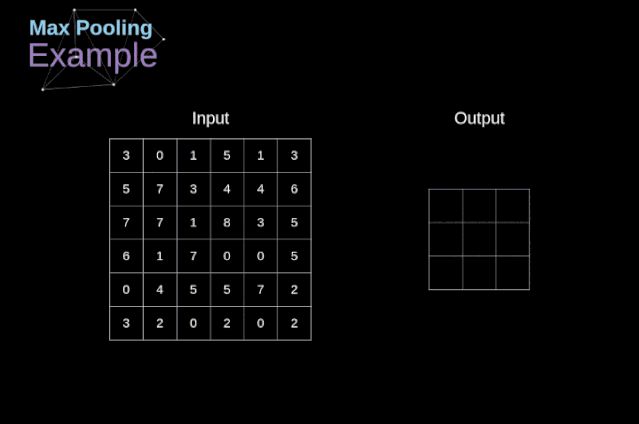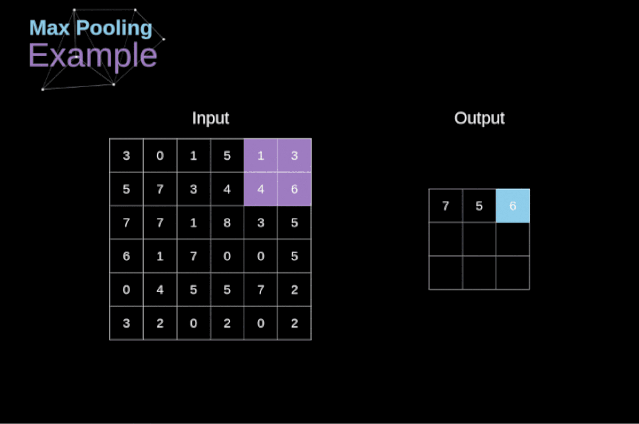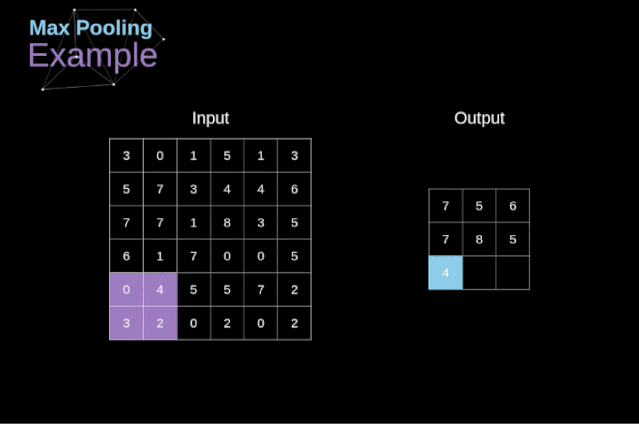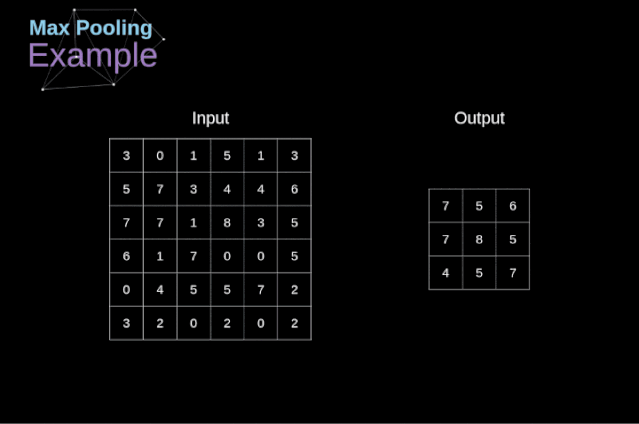
圖12. 最大值池化的例子
池化層反向傳播
在本文中,我們將只討論最大值池化的反向傳播,但是我們將學(xué)習(xí)的規(guī)則只需要稍加調(diào)整就可以適用于所有類型的池化層。由于在這種類型的層中,我們沒有任何必須更新的參數(shù),所以我們的任務(wù)只是適當(dāng)?shù)胤植继荻取U缥覀兯浀玫模谧畲笾党鼗恼騻鞑ブ校覀儚拿總€區(qū)域中選擇最大值,并將它們傳輸?shù)较乱粚印R虼耍苊黠@,在反向傳播過程中,梯度不應(yīng)該影響矩陣中沒有包含在正向傳播中的元素。實際上,這是通過創(chuàng)建一個掩碼來實現(xiàn)的,該掩碼可以記住第一階段中使用的值的位置,稍后我們可以使用該掩碼來傳播梯度。
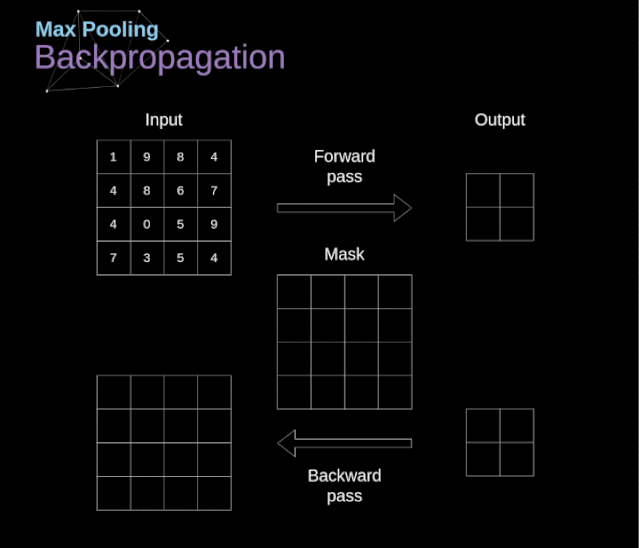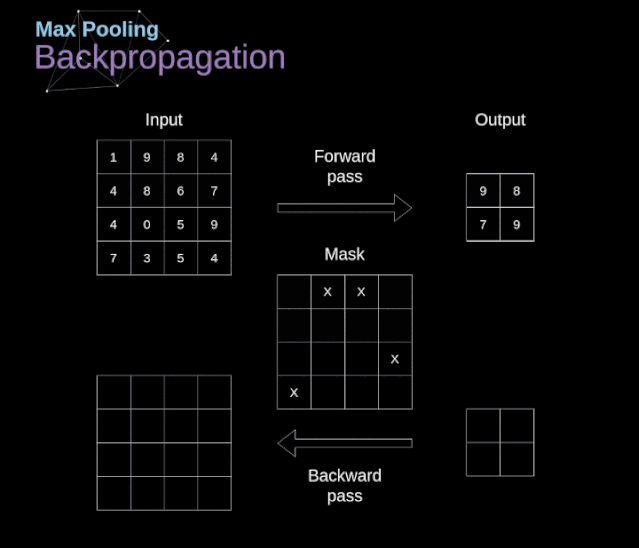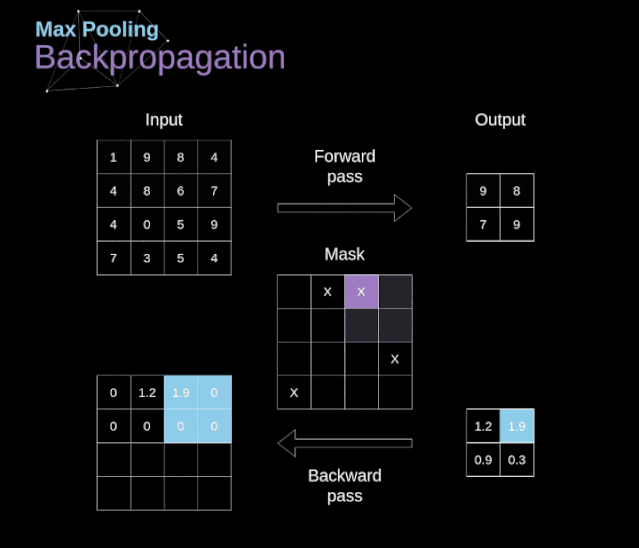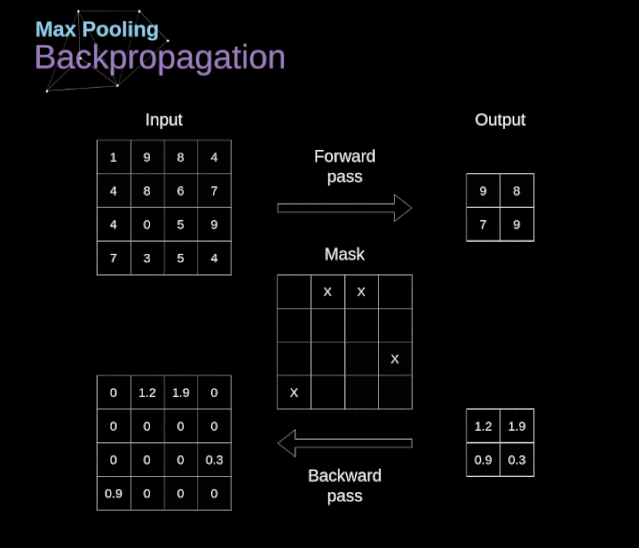
圖13. 最大值池化的反向傳播
結(jié)論
恭喜你能來這里。非常感謝您花時間閱讀本文。如果你喜歡這個帖子,您可以考慮向你的朋友,或者兩個或五個朋友分享。如果你注意到任何錯誤的思維方式,公式,動畫或代碼,請讓我知道。
原文標(biāo)題:圖解:卷積神經(jīng)網(wǎng)絡(luò)數(shù)學(xué)原理解析
文章出處:【微信公眾號:新機器視覺】歡迎添加關(guān)注!文章轉(zhuǎn)載請注明出處。
責(zé)任編輯:haq
-
神經(jīng)網(wǎng)絡(luò)
+關(guān)注
關(guān)注
42文章
4773瀏覽量
100890 -
卷積
+關(guān)注
關(guān)注
0文章
95瀏覽量
18527
原文標(biāo)題:圖解:卷積神經(jīng)網(wǎng)絡(luò)數(shù)學(xué)原理解析
文章出處:【微信號:vision263com,微信公眾號:新機器視覺】歡迎添加關(guān)注!文章轉(zhuǎn)載請注明出處。
發(fā)布評論請先 登錄
相關(guān)推薦




 卷積神經(jīng)網(wǎng)絡(luò)數(shù)學(xué)的原理解析
卷積神經(jīng)網(wǎng)絡(luò)數(shù)學(xué)的原理解析










評論