1、基本概念

要進行機器學習，首先要有數據。從數據中學得模型的過程稱為“學習”或“訓練”。其對應的過程中有幾個基本術語需要知道。

（1）訓練集：模型訓練過程中使用的數據稱為訓練集，其中每個樣本稱為訓練樣本。如：D={X1,X2,X3,…,Xm}。

（2）特征向量：對于每個樣本如Xi = (xi1, xi2,…xin)是一個n維列向量，表示樣本Xi有n個屬性。

2、理論

給定由n個屬性描述而成的m個數據集為：D={X1,X2,X3,…,Xm}，其中Xi = (xi1, xi2,…xin)。

線性模型是試圖學得一個通過屬性的線性組合來進行預測的函數，即：

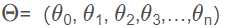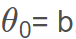其中，其中。當Θ和b確定之后，模型就得以確認。

2.1 線性回歸

2.1.1 什么是回歸

若我們欲預測的是連續值，如：房價，則此類學習任務稱為“回歸”。同理機器學習中還有“分類”任務，即我們欲預測的是離散值，如：“合格”、“不合格”。其中對于二分類任務，稱為“正類”、“負類”；涉及多個類別時，則稱為“多分類”任務。

在線性模型中，我們分為線性回歸與邏輯回歸兩種模型，下面我們對兩種模型分別進行講解分析。

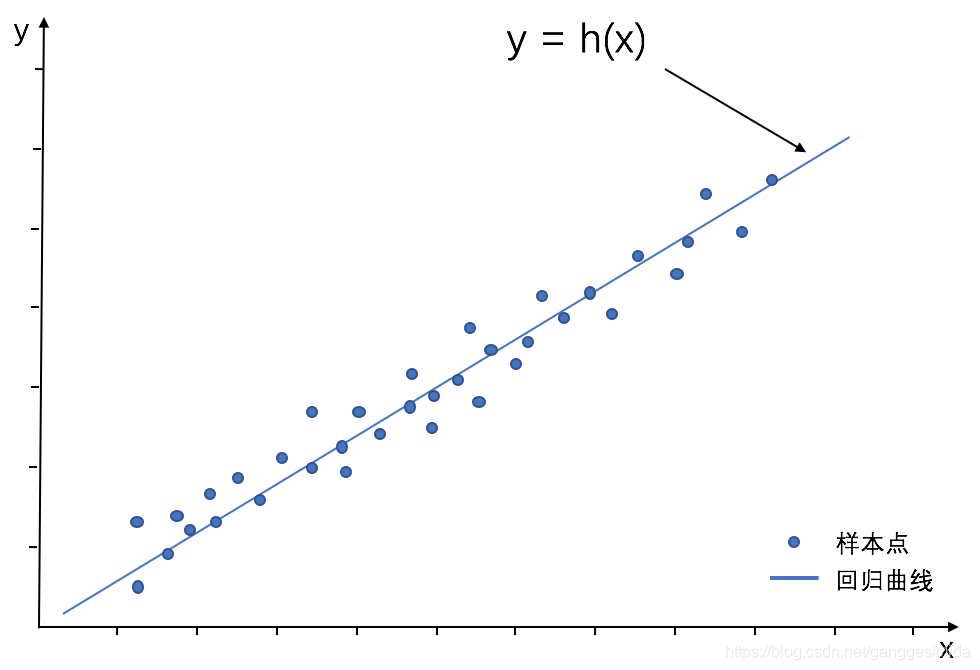
圖1 線性回歸

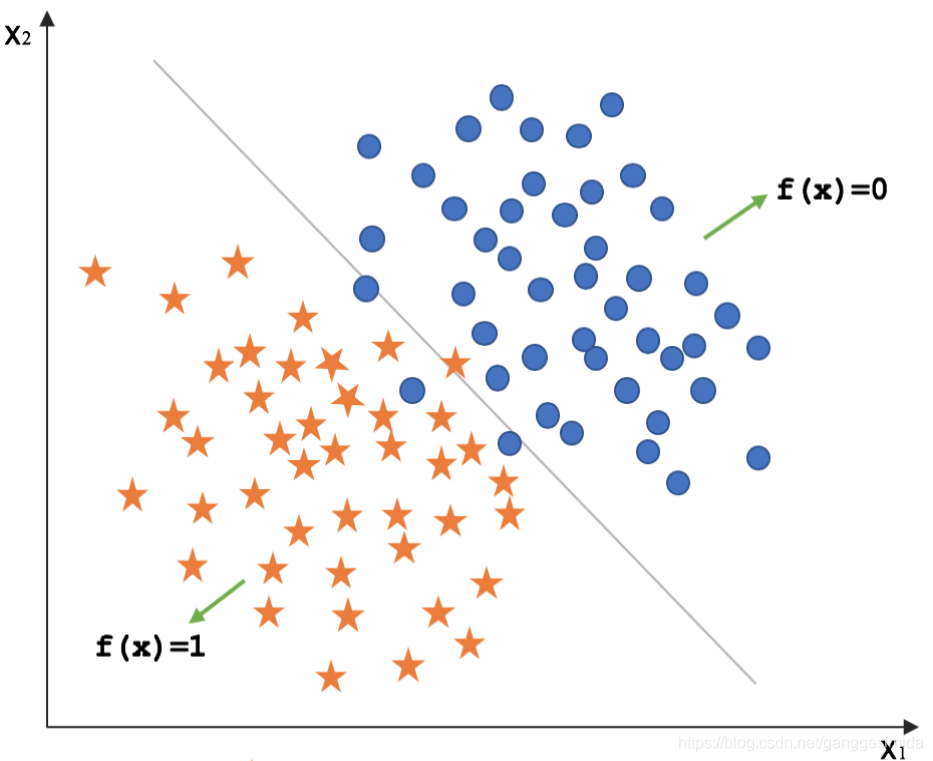
圖2 邏輯回歸

2.1.2 線性回歸推導

1、線性回歸試圖學得：

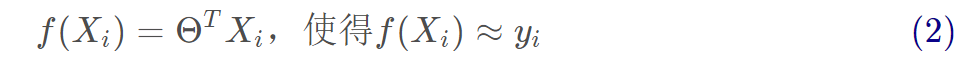
2、參數估計

（1）首先衡量f(X)與Y之間的差別，我們使用均方誤差來衡量。

均方誤差的推導過程如下：

擬合函數為：

矩陣形式為：

真實值和預測值之間通常情況下是會存在誤差的，我們用ε來表示誤差，對于每個樣本都有：

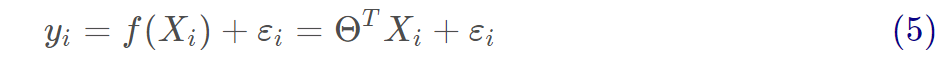
通常我們假設樣本空間中全體樣本中服從一個未知“分布”，我們獲得的每個樣本都是獨立地從這個分布上采樣獲得的，即“獨立同分布”(iid)。

在這里誤差ε是獨立并且具有相同的分布，并且服從均值為0，方差為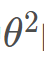的正態分布。

由于誤差服從正態分布，那么有：

將(5)代入到(6)可得：

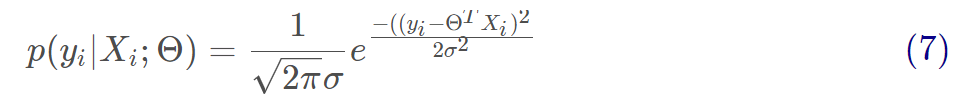
用似然函數進行估計，即求出什么樣的參數跟我們給出的數據組合后能更好的預測真實值，有：

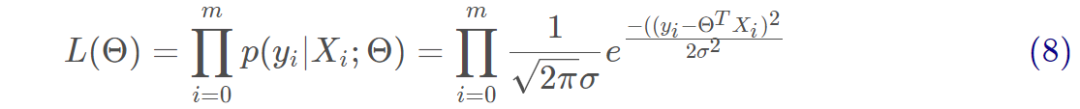
對式8取對數，將連乘轉化為加法為：

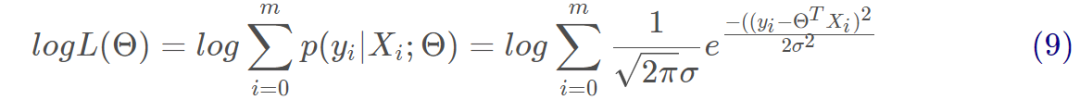
對式9展開化簡為：

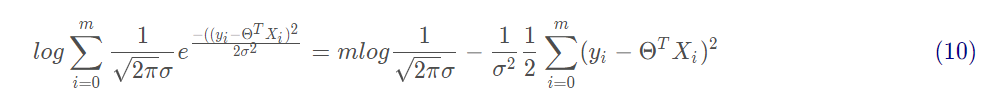
由上式可以看出，右邊第一項為一個常量，似然函數要取最大值，因而第二項越小越好，有：

上述公式相當于最小二乘法的式子，即為均方誤差的式子。

（2）求解Θ：閉式解。

我們試圖讓均方誤差最小化，即

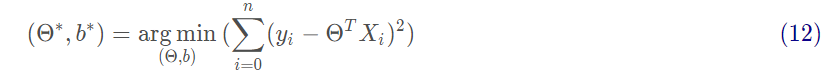
基于均方誤差最小化來進行模型求解的方法稱為“最小二乘法”。在線性回歸中，最小二乘法就是試圖找到一條直線，使所有樣本到直線上的歐式距離之和最小。求解方法為對Θ求偏導。

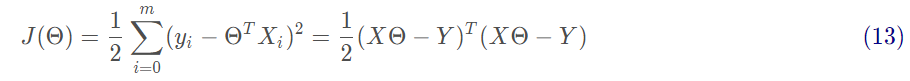
接下來需要對矩陣求偏導，過程如下:

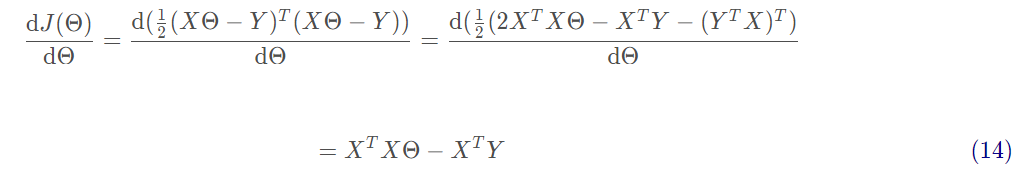
最后令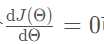可得：

s.t.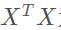為滿秩矩陣時。

在現實中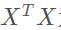往往不是滿秩矩陣，在許多變量中會遇到大量的變量，其數目超過樣本數目，會導致解出多個Θ，常見的做法是引入正則化或者進行降維。

（3）求解Θ：梯度下降法。

沿著函數梯度方向下降最快的就能找到極小值:

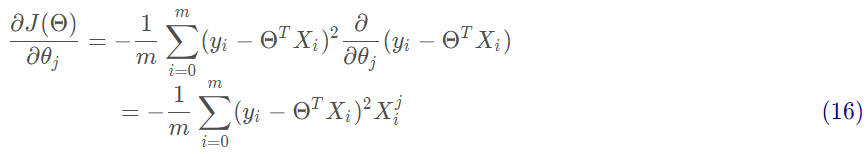
沿著梯度方向更新參數Θ的值:

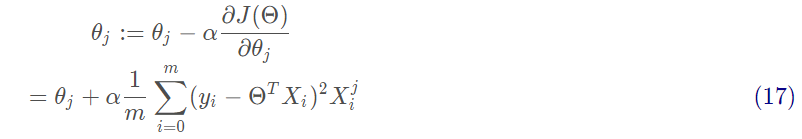
批量梯度下降是用了訓練集中的所有樣本。因此在數據量很大的時候，每次迭代都要遍歷訓練集一遍，開銷會很大，所以在數據量大的時候，可以采用隨機梯度下降法或者批量梯度下降法。

2.2 邏輯回歸

對于分類任務，用線性回歸無法直接進行回歸學習。對于二分類任務，其輸出標記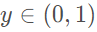，而線性回歸模型產生的預測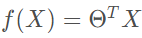值是實值。

2.2.1 對數幾率

一個事件的幾率是指該事件發生的概率與該事件不發生的概率的比值。p(Y=1|X)是指事件發生的條件概率，p(Y=0|X)是指事件不發生的條件概率，則該事件的對數幾率或logit函數是：

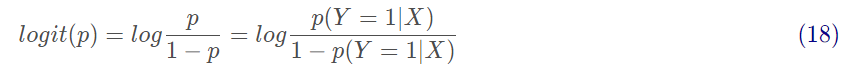
對數幾率范圍為[0,+∞)，當p=1時候，logit(p)=+∞，當p=0時候，logit(p)=0。

對于邏輯回歸而言，有：

將其Θ*X轉換為概率有：

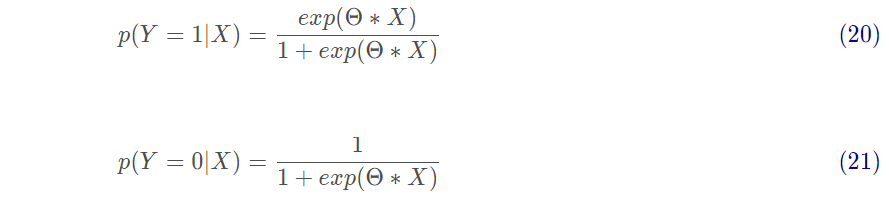
其中

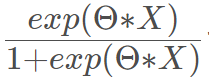
也稱為sigmoid函數，函數圖如下所示：

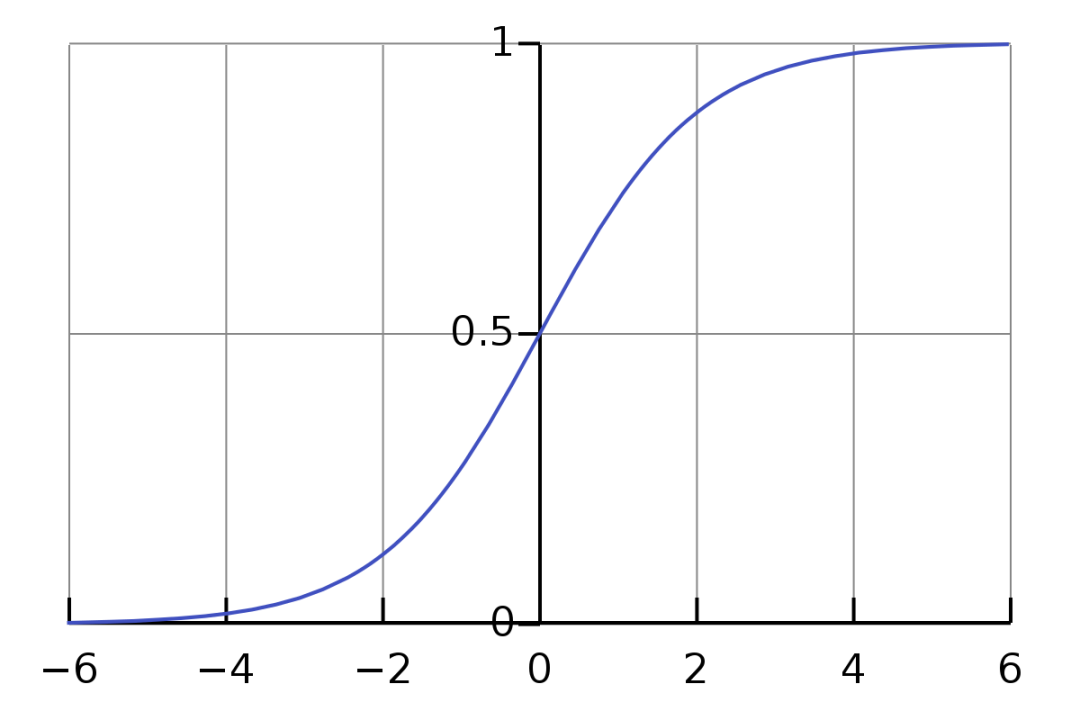
圖3 Sigmoid函數圖

2.2.2 參數估計

在邏輯回歸進行模型學習時，應用極大似然估計來估計模型參數：

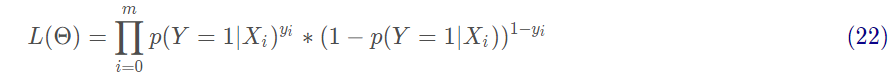
對式22取對數，將連乘轉化為加法為：

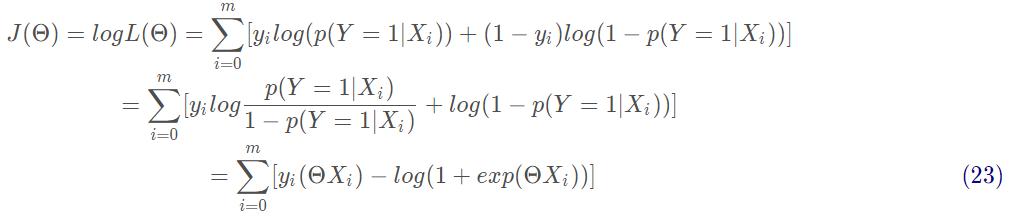
上述公式為求解邏輯回歸的損失函數：交叉熵損失函數。

然后對J(Θ)進行求偏導，求最小值，得到Θ的估計值。沿著函數梯度方向下降就能最快的找到極小值:

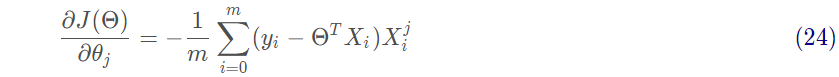
沿著梯度方向更新參數Θ的值:

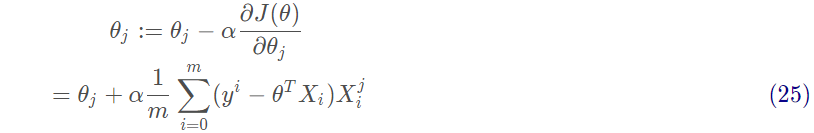
3、實戰

3.1 線性回歸實戰

3.1.1 從零開始實現

1、首先生成數據集

num_inputs = 2 # 數據集的屬性 n : 2num_examples = 1000 # 數據集的樹木 m : 1000true_w = [2, -3.4]true_b = 4.2 features = torch.randn(num_examples, num_inputs, dtype=torch.float32) # 輸入labels = true_w[0]*features[:, 0] + true_w[1]*features[:, 1] + true_b # 標簽labels+=torch.tensor(np.random.normal(0,0.01,size=labels.size()),dtype=torch.float32)#加上一些隨機噪聲

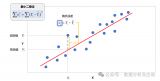
進行可視化后，如下圖所示：

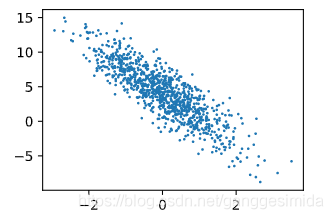
圖4 數據集

2、數據讀取

def data_iter(batch_size, features, labels): num_examples = len(features) indices = list(range(num_examples)) random.shuffle(indices) for i in range(0, num_examples, batch_size): j = torch.LongTensor(indices[i : min(i + batch_size, num_examples)])yieldfeatures.index_select(0,j),labels.index_select(0,j)

如：當batch_size=10時，我們的輸出結果如下所示：

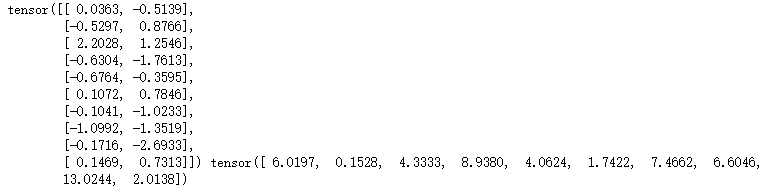
第一個為輸入x（size=[10, 2]），第二個為標簽y（size=[10]）。

3、定義線性回歸模型

def LinReg(X, w, b):returntorch.mm(X,w)+b#torch.mm表示兩個矩陣相乘，[batch_size,num_inputs]*[num_inputs,1]=[batch_size,1]

4、定義損失函數

# 線性回歸模型的損失函數為均方差損失函數def squared_loss(y_hat, y):return(y_hat-y.view(y_hat.size()))**2/2

5、定義優化算法

# 這里我們使用梯度下降算法：sdgdef sgd(params, lr, batch_size): for param in params:param.data-=lr*param.grad/batch_size

6、進行訓練

訓練步驟如下：

（1）首先讀取一個batch_size的數據和標簽
（2）然后進行模型計算；
（3）然后計算損失函數；
（4）然后反向求導優化參數；

lr = 0.03num_epochs = 3net = LinRegloss = squared_loss for epoch in range(num_epochs): # 訓練模型一共需要num_epochs個迭代周期 # 在每一個迭代周期中，會使用訓練數據集中所有樣本一次（假設樣本數能夠被批量大小整除）。X # 和y分別是小批量樣本的特征和標簽 for X, y in data_iter(batch_size, features, labels): l = loss(net(X, w, b), y).sum() # l是有關小批量X和y的損失 l.backward() # 小批量的損失對模型參數求梯度 sgd([w, b], lr, batch_size) # 使用小批量隨機梯度下降迭代模型參數 # 不要忘了梯度清零 w.grad.data.zero_() b.grad.data.zero_() train_l = loss(net(features, w, b), labels)print('epoch%d,loss%f'%(epoch+1,train_l.mean().item()))

最后輸出結果如下所示：

epoch 1, loss 0.044750epoch 2, loss 0.000172epoch3,loss0.000049

3.2 邏輯回歸實戰

邏輯回歸相比線性回歸中，改變的地方為第3步：模型函數 和 第4步：損失函數。

3.2.1 從零實現邏輯回歸

3、定義邏輯回歸模型

def sigmoid(X, w, b): ''' 定義sigmoid函數 :param x: 參數x 返回計算后的值 ''' z = torch.mm(X, w) + breturn1.0/(1+np.exp(-z))

4、定義損失函數

# 在邏輯回歸中，我們使用的是對數損失函數（交叉熵損失函數）def BCE_loss(y_hat, y): ''' 損失函數 :param y_hat: 預測值 :param y: 實際值 loss ''' m = np.shape(y_hat)[0] loss = 0.0 for i in range(m): if y_hat[i, 0] > 0 and (1 - y_hat[i, 0]) > 0: loss-= (y[i, 0] * np.log(y_hat[i, 0]) + (1 - y[i, 0]) * np.log(1 - y_hat[i, 0])) else: loss-= 0.0returnloss/m

責任編輯：xj

原文標題：【機器學習】線性回歸與邏輯回歸的理論與實戰

文章出處：【微信公眾號：深度學習自然語言處理】歡迎添加關注！文章轉載請注明出處。