如果您不是光學專業的，或者是文科生，那么您想到光的干涉和衍射第一反應應該是很多公式對不對？頭好大是不是？好，那么今天我們就不用一個公式來重新解讀光的干涉和衍射。
光，也叫電磁波，他的表現形式我們通常用正弦曲線來表示，如下圖：

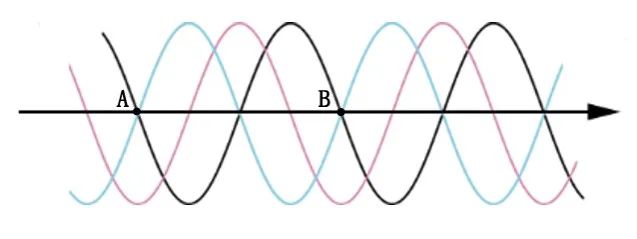
圖1電磁波曲線

光有很多物理參數，其中有一個如從A點到B點的長度我們叫做波長，波長與頻率相關，即與光的顏色有關。而光波從A點走到B點，等于走了一個波長的長度，相位剛好也改變了2π，這是最基本的知識應該不用再多做介紹。
好，接下來進入正題，我們來看看光的干涉是如何發生的。以圖1為例，圖中黑色和藍色的電磁波，在空間發生干涉，會發生什么？剛好干涉相消；如果是藍色和紅色的電磁波發生干涉，那么就會形成一個新的幅值更高的正弦波。這里就可以簡單推斷出2個干涉需要滿足的條件：第一、振動方向相同，如果黑色是紙面內上下振動，藍色如果改成垂直紙面振動，那么它倆毫無關系；第二，頻率相同以及相位差恒定，只有滿足這2個條件，才能在空間中形成亮暗相間的干涉條紋。

問題來了！第一個問題，前面提到的黑色和藍色電磁波發生干涉，剛好干涉相消，從干涉條紋來看是一片黑，即沒有任何光強，也就是意味著沒有能量了？這是不是違背了能量守恒定律？答案當然是不違背的。其實我們分析的都只是電場分量，而真正光的形式是這樣的，能量不僅只有電場，還有磁場的：

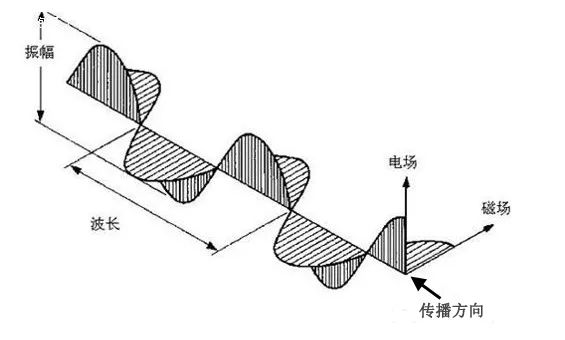
圖2電磁波傳播形式（向左）

好，現在分為二種情況分析剛才的干涉相消：對向而行和同向而行；
先分析對向而行，結合圖2和圖3（傳播方向相反），如果要讓干涉相消，即電場矢量方向相反，那么我們就會發現磁場分量的振動方向是相同的，所以電場分量干涉相消，其實是把電場的能量全部轉移到磁場上去了，所以總能量依舊是守恒的。

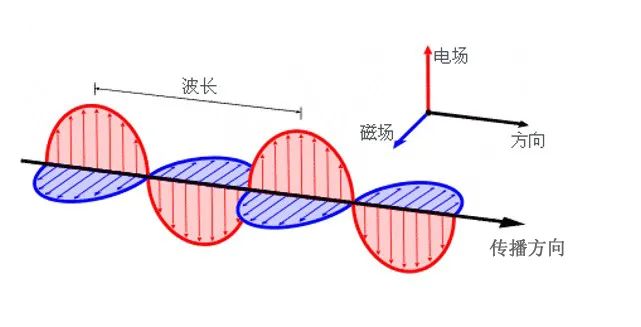
圖3電磁波向右傳播

接下來分析同向而行的情況，如果你用上面的方式套用的話，你會發現電場矢量干涉相消，磁場也干涉相消，能量真的消失了？不是，原因在什么地方？繼續舉例子，看圖說話：

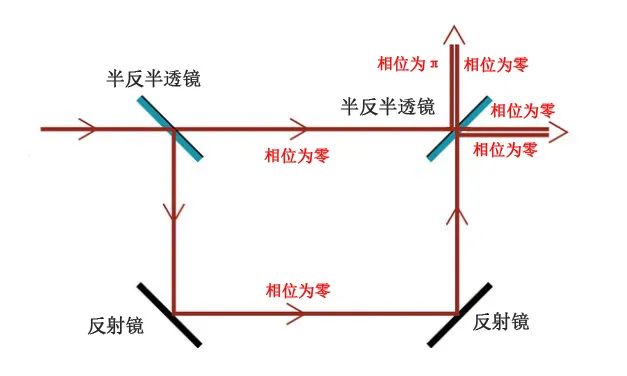
圖4電磁波干涉示意圖

我們通過光學系統讓光產生干涉，發現在右側半反半透鏡的上下2個面總會有一個干涉相消、一個干涉相漲。這里需要說明一點，當光從光疏介質入射到光密介質反射時，會有半波損失，即會改變π相位，從光密介質入射到光疏介質時，相位不發生變化。所以，總結一下，光干涉本質不是光子的直接湮滅，而是能量的再分配！

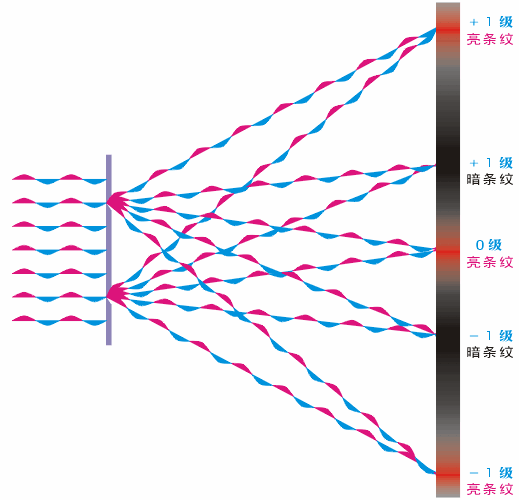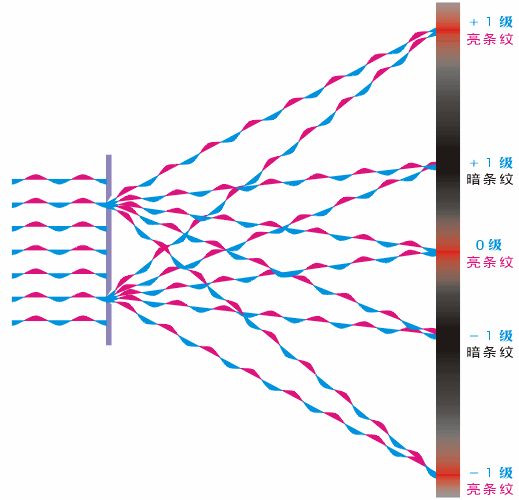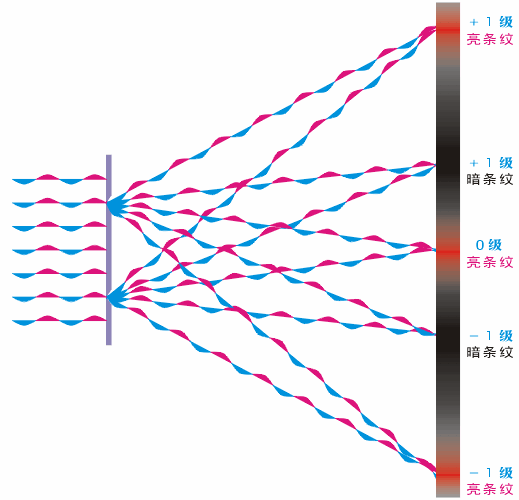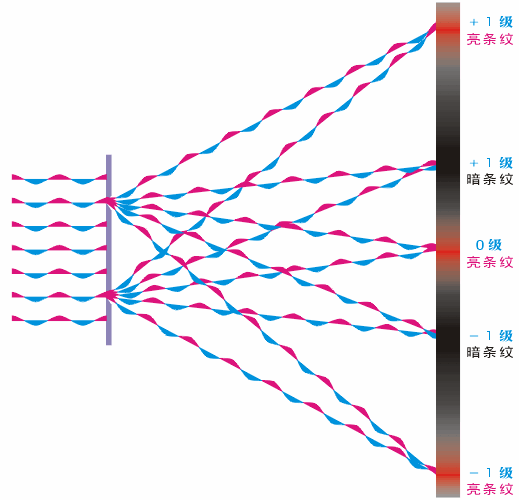
圖5干涉動態圖（圖片來源于網絡）

前面我們討論了干涉的原理，如圖5所示，當2個光源到達像面的距離相差半個波長的偶數倍時，就是亮條紋；如果距離相差半個波長為奇數倍時，為暗條紋。好，接下來我們再來看衍射是如何發生的？中學的時候我們就學過，當光通過小孔的時候，光會發生衍射，而且孔越小，衍射現象越明顯。

圖6單縫衍射示意圖（圖片來源于網絡）

圖7單縫衍射原理圖（圖片來源于網絡）

那么，我們再來看衍射光的理論分析圖（圖7），衍射光在經過小孔AB后會朝各個方向傳播，假設衍射光是平行傳播的，那么到達像面的是O點，顯而易見，到達這個點的衍射光是沒有相位差的，自然是亮條紋。接著增大θ角，顯然A點衍射光和B點的衍射光達到像面Q點的光程是不一樣的，所以我們用半波帶法來分割這個衍射光，即光程差為半個波長為寬度視作一個光源，那么AA1可以看做一個子光源，A1A2可以看做一個子光源，自然這2個光源的相位剛好相反，即干涉相消，所以隨著θ角的增大，光程差會發生變化，條紋會亮暗相間。

接下來回答為什么孔越小，衍射越明顯。反一下就是孔越大，衍射現象越不明顯。衍射現象明不明顯，我們一般是用光的強度來判斷。如圖7，如果小孔AB可以劃分為11個半波帶，那么其中10個干涉相消，只剩1個還在，那么這一級應該是亮條紋，能量用面積上來理解就是1/11；如果小孔AB只可劃分5個半波帶，那么亮條紋能量面積是1/5。所以得出結論：孔越小，衍射越明顯。根據這個半波帶法，還可以得出另一個結論：當小孔大小不變的情況下，波長越長，被分割的半波帶數量越少，自然單個半波帶能量面積越大，衍射現象越明顯。

單縫衍射介紹完畢，接下來就輪到多縫衍射了。多縫衍射顯然應該是單縫衍射以及干涉的結合體，所以我們就得到了下面這個圖：

圖8多縫衍射原理圖（圖片來源于網絡）

多縫衍射最經典的例子就是光柵。那我們現在以光纖光柵為例，來看看光纖光柵是怎么工作的以及有什么用途。

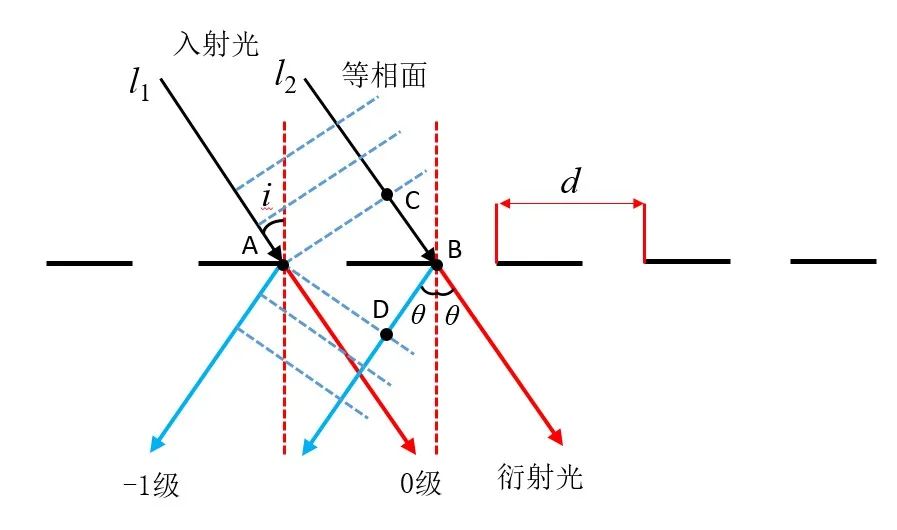
圖9光柵衍射原理圖

圖9為光柵干涉衍射原理圖，把它代入到光纖中，我們就可以簡化成下圖：

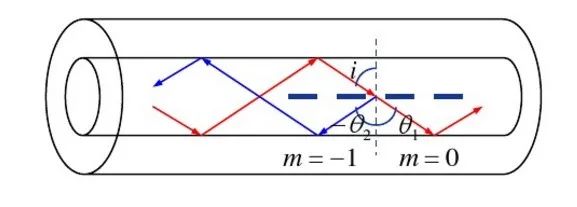
圖10布拉格光纖光柵原理（圖片來源于網絡）

根據上一期光纖傳感中的光傳輸原理，不僅需要滿足全反射條件，而且需要滿足一定的相位條件。這個相位條件，也可以根據圖9推導出來，即兩束光的光程差要是波長的整數倍才能干涉相漲：

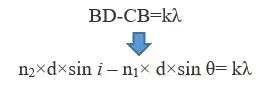
由于衍射光0級和1級的光強相對大一點，所以2級以后的衍射光幾乎忽略不計。當取k=1時，我們可以得到衍射光的波長與光柵周期d和折射率、角度有關系。顯然，如果要1級衍射光能夠在光纖中反向傳輸，那么光線必須和入射光線要平行（光纖中的相位匹配條件）。根據公式想象一下，我們總會有那么個波長的光線滿足這個角度后向傳輸，這個波長我們就叫做布拉格波長，這種反射式的光纖光柵也叫做布拉格光纖光柵。這里需要再說明下，光其實是很神奇的，各個波長的光都會有各自的衍射光，但是由于其他波長的衍射光沒有滿足光纖傳輸干涉相漲的條件，所以就不往1級衍射光這個方向走了，全部往0級衍射光方向傳輸。

問題又來了，光纖中的光居然可以反向傳輸，那衍射光一定是反向的嗎？不一定，根據上面的公式，在波長一定的情況下，顯然光柵周期d和角度θ成反比，所以當光柵周期d足夠大的時候，我們發現θ角變成正向傳輸了，如下圖所示。傳輸原理同上，我們同樣會得到這么個波長使得其滿足光纖中傳輸的條件，且這個波長傳輸的角度不再是在光纖纖芯中全反射，而變成了在包層中全反射，這就是包層模的模式。而包層模式的光會在很短距離內衰減損耗掉，所以在光纖的接收端我們得到了除了這個波長的光信號，于是我們也把這種光纖叫做透射式光纖光柵，亦叫作長周期光纖光柵；而布拉格光纖光柵，即反射式光纖光柵也叫作短周期光纖光柵。

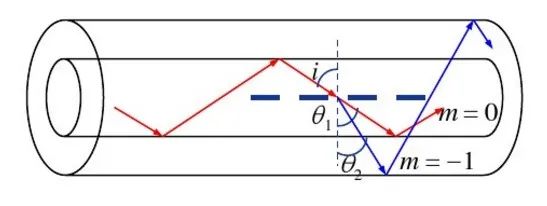
圖11長周期光纖光柵原理（圖片來源于網絡）

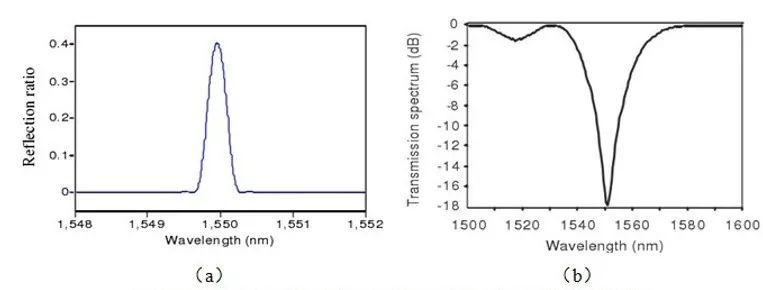
圖12（a）布拉格光纖光柵反射譜;（b）長周期光纖光柵透射譜（圖片來源于網絡）

責任編輯：xj

原文標題：重溫經典：簡讀光干涉、衍射原理

文章出處：【微信公眾號：微波射頻網】歡迎添加關注！文章轉載請注明出處。