理想的PID算法往往不能滿足實(shí)際使用中的很多場(chǎng)景,比如積分飽和的問(wèn)題,因此需要在此基礎(chǔ)上對(duì)積分器做抗飽和處理,積分anti windup的優(yōu)化。這不,隆哥這次面試,直接掛在這么基礎(chǔ)的知識(shí)點(diǎn)上,腸子悔青,在這里簡(jiǎn)單總結(jié)一下。
1、什么是積分飽和
積分飽和(Integral windup或integrator windup)是指PID控制器或是其他有積分器的控制器中可能會(huì)發(fā)生的一種現(xiàn)象。
這種現(xiàn)象往往發(fā)生在誤差有大幅變化(例如大幅增加),積分器因?yàn)檎`差的大幅增加有很大的累計(jì)量,因?yàn)榉e分器的輸出滿足下式;
離散化形式表示為:
所以隨著時(shí)間的增加,每次累積較大的誤差 ,很容易造成積分飽和并產(chǎn)生較大的過(guò)沖,而且當(dāng)誤差變?yōu)樨?fù)時(shí),其過(guò)沖仍維持一段時(shí)間之后才恢復(fù)正常的情形。
2、實(shí)際的例子
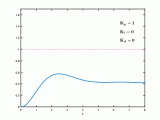
這里舉一個(gè)直流電機(jī)調(diào)速例子,先看下圖;
隆哥設(shè)定了轉(zhuǎn)速為 ,這里可以是100 rpm,但是由于某種原因電機(jī)一開始堵轉(zhuǎn)了,所以反饋的轉(zhuǎn)速 為0;
這時(shí)候仍然處于堵轉(zhuǎn)狀態(tài),那偏差 就會(huì)一直處于很大的狀態(tài),積分器對(duì)偏差 進(jìn)行累積,便迅速達(dá)到一個(gè)很大的值,導(dǎo)致PID的輸出已經(jīng)接近輸出的 上限,導(dǎo)致最終輸出的PWM的占空比很大;
此時(shí),堵轉(zhuǎn)忽然消失,但是前面提到PID的輸出已經(jīng)接近輸出的 上限,因此電機(jī)轉(zhuǎn)速也急劇上升,當(dāng) 時(shí), ,此時(shí)偏差都處于負(fù)數(shù)狀態(tài);
雖然誤差變成負(fù)數(shù),并且積分器開始累加負(fù)數(shù),但是由于之前積分器累積的值已經(jīng)很大,于是,PID依然會(huì)保持較大的輸出一段時(shí)間,從而產(chǎn)生了很大的過(guò)沖;
通常會(huì)產(chǎn)生的輸出如下圖所示;
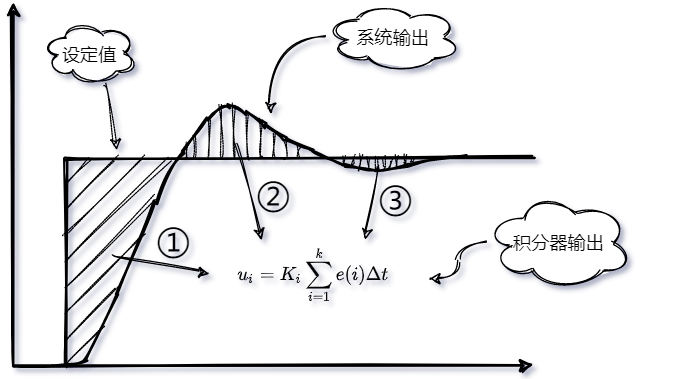
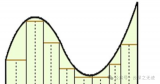
從圖中我們不難發(fā)現(xiàn),這里有三個(gè)過(guò)程;
過(guò)程①:因?yàn)檫@個(gè)過(guò)程存在 較大幅度變化的誤差,因此積分器累積了較大的值,從圖中可以看到,積分器的面積比較大(陰影部分);過(guò)程②:此時(shí)積分已經(jīng)飽和,產(chǎn)生了較大的過(guò)沖,并且在較長(zhǎng)的一段時(shí)間內(nèi),一直處于過(guò)沖的狀態(tài);過(guò)程③:積分脫離飽和狀態(tài),產(chǎn)生了積極的調(diào)節(jié)作用,消除靜差,系統(tǒng)輸出達(dá)到設(shè)定值;
3、負(fù)面影響
積分器的作用是消除系統(tǒng)穩(wěn)態(tài)誤差,如果出現(xiàn)積分飽和,往往會(huì)對(duì)系統(tǒng)造成負(fù)面的影響;
系統(tǒng)輸出會(huì)產(chǎn)生較大的過(guò)沖(超調(diào)量);
如果產(chǎn)生正向飽和(圖一所示)則系統(tǒng)對(duì)于反向的變化會(huì)偏慢;
系統(tǒng)產(chǎn)生了較大的過(guò)沖 ,并且較大的一段時(shí)間 都處于過(guò)沖的狀態(tài);具體如下圖所示;
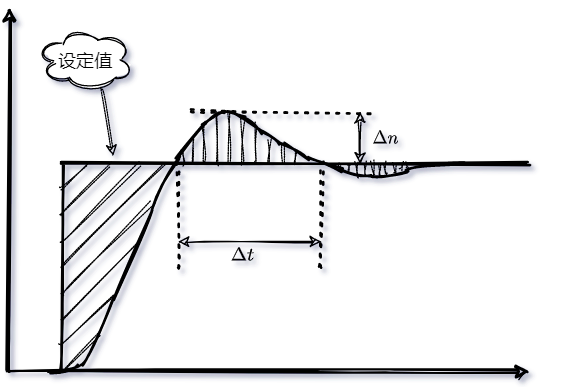
4、如何防止積分飽和
為了防止PID控制器出現(xiàn)積分飽和,需要在算法加入抗積分飽和(anti-integral windup)的算法;通常有以下幾種措施;
積分分離或者稱為去積分算法;
在飽和的時(shí)候?qū)⒎e分器的累計(jì)值初始化到一個(gè)比較理想的值;
若積分飽和因?yàn)槟繕?biāo)值突然變化而產(chǎn)生,將目標(biāo)值以適當(dāng)斜率的斜坡變化可避免此情形;
將積分累計(jì)量限制上下限,避免積分累計(jì)量超過(guò)限制值;
如果 PID輸出已經(jīng)飽和,重新計(jì)算積分累計(jì)量,使輸出恰好為合理的范圍;
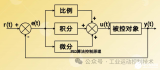
TI文檔中的方法
下面是TI的位置式PI算法所做的改進(jìn),如下圖所示;
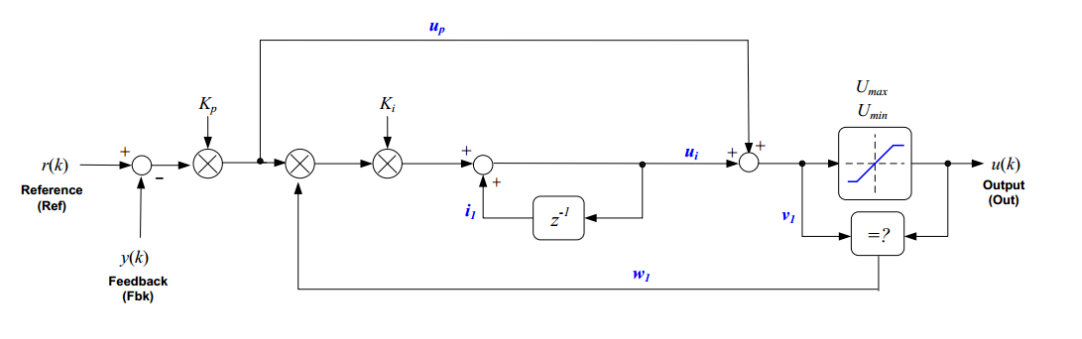
比例部分的輸出:
積分部分的輸出:
未做處理的PID輸出:
最終PID輸出 :
抗積分飽和用的系數(shù)
根據(jù)我的理解,由上述輸出和①式可知,判斷系統(tǒng)是否處于飽和的狀態(tài);
如果 ,說(shuō)明積分器處于飽和狀態(tài),此時(shí)使 系數(shù)為0,這樣防止積分進(jìn)一步進(jìn)行累積。
反計(jì)算抗飽和法
反計(jì)算Anti-Windup法,簡(jiǎn)稱AW法,就是在輸出限幅部分根據(jù)輸入信號(hào)和輸出信號(hào)的差值,把 作為反饋值輸入到積分部分,從而達(dá)到抑制積分飽和現(xiàn)象的目的;
具體如下圖所示;
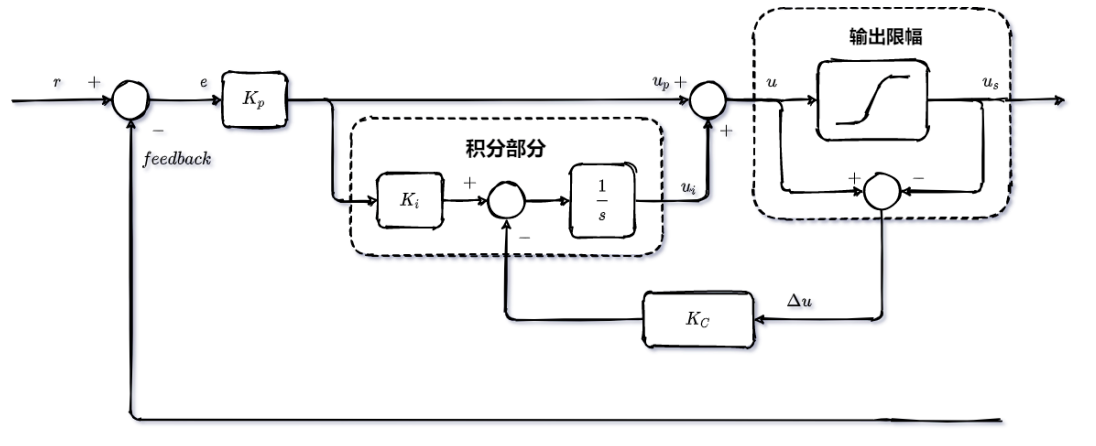
不難發(fā)現(xiàn),在輸出未飽和的情況下, 因此不會(huì)對(duì)積分器造成影響;當(dāng)系統(tǒng)發(fā)生飽和時(shí),則 ;
現(xiàn)在假設(shè)此時(shí)為正向飽和,則 ,那么 ,所以最終將 反饋到積分部分;那么從圖中可知,相當(dāng)于從 中減去了 ,這樣可以削弱積分,讓它退出飽和的狀態(tài);
關(guān)于 系數(shù), 越大,積分器退出飽和的作用越強(qiáng),反之則越弱;
當(dāng)然,積分抗飽和的方法還有很多 遇限積分削弱法,遇限保留積分法 ,這只是其中的一種,下面給出TI的位置式PID算法,增量式的抗飽和處理也是類似的做法。
5、PID算法(抗飽和)
TI的算法中只實(shí)現(xiàn)了比例和積分,如果需要微分項(xiàng),可以去除結(jié)尾部分的注釋;
/* ===========
File name: PID_REG3.H (IQ version)
=*/ #ifndef __PIDREG3_H__ #define __PIDREG3_H__ typedef struct { _iq Ref;
// Input: Reference input _iq Fdb;
// Input: Feedback input _iq Err; // Variable: Error
_iq Kp; // Parameter: Proportional gain _iq Up; // Variable: Proportional output
_iq Ui; // Variable: Integral output _iq Ud; // Variable: Derivative output
_iq OutPreSat; // Variable: Pre-saturated output _iq OutMax; // Parameter: Maximum output
_iq OutMin; // Parameter: Minimum output _iq Out; // Output: PID output
_iq SatErr; // Variable: Saturated difference _iq Ki; // Parameter: Integral gain
_iq Kc; // Parameter: Integral correction gain _iq Kd; // Parameter: Derivative gain
_iq Up1; // History: Previous proportional output } PIDREG3;
typedef PIDREG3 *PIDREG3_handle;
/*-----------------------------------------------------------------------------
Default initalizer for the PIDREG3 object.
--*/ #define PIDREG3_DEFAULTS { 0, \
0, \
0, \
_IQ(1.3), \
0, \
0, \
0, \
0, \
_IQ(1), \
_IQ(-1), \
0, \
0, \
_IQ(0.02), \
_IQ(0.5), \
_IQ(1.05), \
0, \
}
/*------------------------------------------------------------------------------
PID Macro Definition
------------------------------------------------------------------------------*/
#define PID_MACRO(v) \
v.Err = v.Ref - v.Fdb; /* Compute the error */ \
v.Up= _IQmpy(v.Kp,v.Err); /* Compute the proportional output */ \
v.Ui= v.Ui + _IQmpy(v.Ki,v.Up) + _IQmpy(v.Kc,v.SatErr); /* Compute the integral output */ \
v.OutPreSat= v.Up + v.Ui; /* Compute the pre-saturated output */ \
v.Out = _IQsat(v.OutPreSat, v.OutMax, v.OutMin); /* Saturate the output */ \
v.SatErr = v.Out - v.OutPreSat; /* Compute the saturate difference */ \
v.Up1 = v.Up;
/* Update the previous proportional output */ #endif // __PIDREG3_H__ // Add the lines below if derivative output is needed following the integral update //
v.Ud = _IQmpy(v.Kd,(v.Up - v.Up1)); // v.OutPreSat = v.Up + v.Ui + v.Ud;
編輯:hfy
-
直流電機(jī)
+關(guān)注
關(guān)注
36文章
1710瀏覽量
70200 -
PID
+關(guān)注
關(guān)注
35文章
1472瀏覽量
85547 -
積分器
+關(guān)注
關(guān)注
4文章
100瀏覽量
28459
發(fā)布評(píng)論請(qǐng)先 登錄
相關(guān)推薦
如何使用Python實(shí)現(xiàn)PID控制
PID控制中的反饋機(jī)制解析
如何調(diào)節(jié)PID參數(shù) PID控制器的調(diào)試方法
PID控制的優(yōu)缺點(diǎn)分析 PID參數(shù)調(diào)節(jié)的常見方法
如何使用PID進(jìn)行溫度控制
什么是PID控制器及其應(yīng)用
LM324對(duì)小電阻r上的電壓進(jìn)行放大、積分,正向飽和的原因?
什么是PID?PID各個(gè)參數(shù)有什么作用?
PID效應(yīng)的成因及抑制方法
什么是pid控制原理 pid各個(gè)參數(shù)對(duì)系統(tǒng)的影響
什么是PID控制器?PID控制器控制器中的積分控制是什么?




 一文解析PID的積分抗飽和原理
一文解析PID的積分抗飽和原理











評(píng)論