許多ADC用于測量靜態信號的電平或大小。應用包括重量，壓力和溫度的測量。這些應用涉及需要高分辨率和高精度的低電平信號。一個示例是可以承受5 kg負載，但仍可將測量結果解析為10毫克的秤。

當使用高分辨率ADC時，需要了解與轉換過程相關的誤差和噪聲。本應用筆記的目的是展示如何使用直方圖分析來量化靜態性能。收集數據樣本集并用于測量噪聲和偏移。統計技術用于確定與估計相關的“優”和置信區間。解決平均問題是減少不確定性和提高分辨率的一種手段。

噪聲直方圖說明

通常，不指定描述ADC噪聲的PDF。該PDF可以通過靜態測試進行估算。該估計的PDF實際上是隨機變量相對于各個變量的發生的直方圖。對于ADC，隨機變量是生成的數字代碼，因此，將針對每個離散代碼繪制每個代碼出現的頻率。

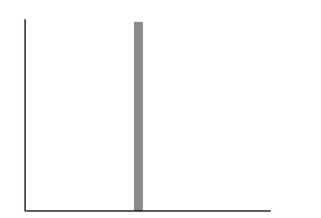
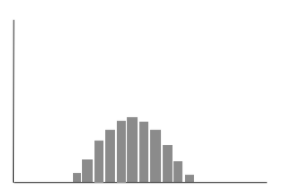
在無噪聲ADC中，特定輸入電壓的輸出代碼將始終為相同的值。無噪聲轉換器的直方圖如圖1所示。如果ADC中存在噪聲源，則輸出代碼的直方圖包含多個值。圖2的直方圖表明，單個輸入的輸出可以是11種可能的代碼之一。

由隨機效應產生的電噪聲會形成高斯分布或正態分布，這是稱為正態曲線的鐘形曲線。高斯PDF是連續的，并且完全由平均值（μ）和方差（σ2）來確定。高斯PDS由以下公式定義：

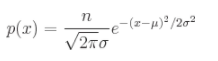
實際PDF的n= 1。

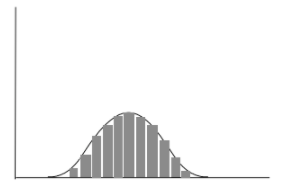
n的其他值可縮放PDF以適合樣本集。圖3中顯示的數據可用于估計PDF。圖3繪制了帶有噪聲的ADC直方圖及其估計的PDF。均值和方差是從樣本數據集中估計的。根據這些PDF參數，可以量化ADC的性能。平均值是期望值或平均值。它用于測量偏移誤差。方差描述了均值分布的變異性。它用作不確定性或噪聲的度量。方差的平方根稱為標準偏差（σ），它是有效噪聲或rms噪聲的量度。峰峰值噪聲可以從均方根噪聲值確定。

高斯PDF不能用于測量所有類型的噪聲。當使用正態分布或高斯分布來估計PDF時，噪聲必須是隨機的。圖4示出了非隨機噪聲的直方圖。注意，直方圖分布不具有熟悉的鐘形。直方圖可能是60 Hz線路干擾或其他類型的正弦噪聲的結果。PDF類似于正弦波，具有“尖峰形”分布。

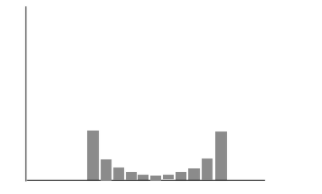
圖5是不具有高斯形狀的PDF的另一個示例。此處的原因是由于ADC的差分非線性（DNL）較差。DNL較差會導致代碼寬度不均勻，從而使分布偏斜。Δ-Σ和自校準ADC具有良好的DNL規格。良好的DNL對于使用平均以提高分辨率的應用程序非常重要。

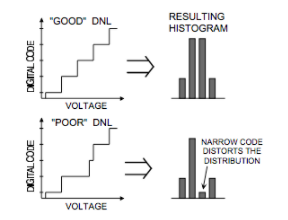
直方圖必須具有鐘形分布，否則估計的高斯PDF將不相關或估計的高斯PDF將不與實際系統相關。優良作法是查看噪聲分布并驗證是否正在分析隨機噪聲。如果噪聲不是隨機的，則不能使用高斯PDF方程對直方圖進行建模。

編輯：hfy