一、隨機失活（Dropout)

具體做法：在訓練的時候，隨機失活的實現方法是讓神經元以超參數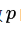的概率被激活或者被設置為 0。如下圖所示：

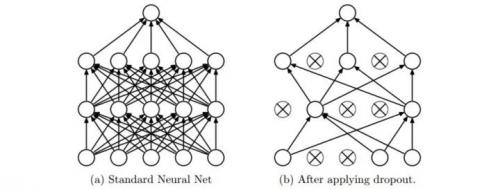
Dropout 可以看作是 Bagging 的極限形式，每個模型都在當一種情況中訓練，同時模型的每個參數都經過與其他模型共享參數，從而高度正則化。在訓練過程中，隨機失活也可以被認為是對完整的神經網絡抽樣出一些子集，每次基于輸入數據只更新子網絡的參數（然而，數量巨大的子網絡們并不是相互獨立的，因為它們都共享參數）。在測試過程中不使用隨機失活，可以理解為是對數量巨大的子網絡們做了模型集成（model ensemble），以此來計算出一個平均的預測。

關于 Dropout 的 Motivation：一個是類似于性別在生物進化中的角色：物種為了生存往往會傾向于適應這種環境，環境突變則會導致物種難以做出及時反應，性別的出現可以繁衍出適應新環境的變種，有效的阻止過擬合，即避免環境改變時物種可能面臨的滅絕。還有一個就是正則化的思想，減少神經元之間復雜的共適應關系，減少權重使得網絡對丟失特定神經元連接的魯棒性提高。

這里強烈推薦看下論文原文。雖然是英文的，但是對于更深刻的理解還是有很大幫助的！

二、圖像數據的預處理

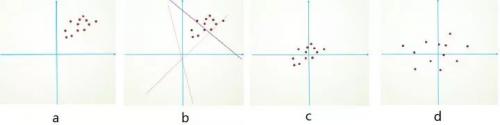
為什么要預處理：簡單的從二維來理解，首先，圖像數據是高度相關的，假設其分布如下圖 a 所示(簡化為 2 維)。由于初始化的時候，我們的參數一般都是 0 均值的，因此開始的擬合 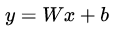，基本過原點附近(因為 b 接近于零)，如圖 b 紅色虛線。因此，網絡需要經過多次學習才能逐步達到如紫色實線的擬合，即收斂的比較慢。如果我們對輸入數據先作減均值操作，如圖 c，顯然可以加快學習。更進一步的，我們對數據再進行去相關操作，使得數據更加容易區分，這樣又會加快訓練，如圖 d。

下面介紹下一些基礎預處理方法：

歸一化處理

均值減法（Mean subtraction）:它對數據中每個獨立特征減去平均值，從幾何上可以理解為在每個維度上都將數據云的中心都遷移到原點。（就是每個特征數據減去其相應特征的平均值）

歸一化（Normalization）;先對數據做零中心化（zero-centered）處理，然后每個維度都除以其標準差。

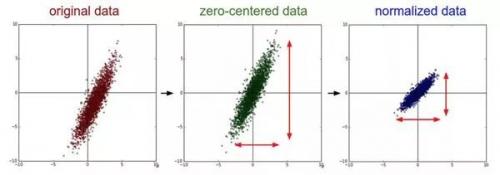
（中間零中心化，右邊歸一化）

PCA 和白化（Whitening）

白化（Whitening）:白化操作的輸入是特征基準上的數據，然后對每個維度除以其特征值來對數值范圍進行歸一化。該變換的幾何解釋是：如果數據服從多變量的高斯分布，那么經過白化后，數據的分布將會是一個均值為零，且協方差相等的矩陣

特征向量是按照特征值的大小排列的。我們可以利用這個性質來對數據降維，只要使用前面的小部分特征向量，丟棄掉那些包含的數據沒有方差的維度。這個操作也被稱為主成分分析（ Principal Component Analysis）簡稱 PCA）降維

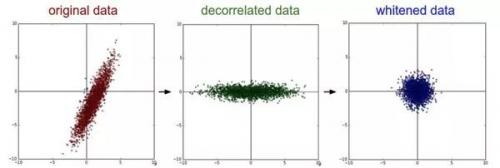
(中間是經過 PCA 操作的數據，右邊是白化)

需要注意的是:

對比與上面的中心化，與 pca 有點類似，但是不同的是，pca 把數據變換到了數據協方差矩陣的基準軸上（協方差矩陣變成對角陣），也就是說他是軸對稱的，但簡單的零中心化，它不是軸對稱的；還有 PCA 是一種降維的預處理，而零中心化并不是。

常見錯誤:任何預處理策略（比如數據均值）都只能在訓練集數據上進行計算，算法訓練完畢后再應用到驗證集或者測試集上。例如，如果先計算整個數據集圖像的平均值然后每張圖片都減去平均值，最后將整個數據集分成訓練 / 驗證 / 測試集，那么這個做法是錯誤的。應該怎么做呢？應該先分成訓練 / 驗證 / 測試集，只是從訓練集中求圖片平均值，然后各個集（訓練 / 驗證 / 測試集）中的圖像再減去這個平均值。

三、Batch Normalization

原論文中，作者為了計算的穩定性，加了兩個參數將數據又還原回去了，這兩個參數也是需要訓練的。說白了，就是對每一層的數據都預處理一次。方便直觀感受，上張圖：

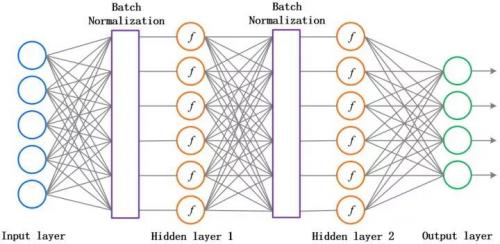
這個方法可以進一步加速收斂，因此學習率可以適當增大，加快訓練速度；過擬合現象可以得倒一定程度的緩解，所以可以不用 Dropout 或用較低的 Dropout，而且可以減小 L2 正則化系數，訓練速度又再一次得到了提升。即 Batch Normalization 可以降低我們對正則化的依賴程度。

還有要注意的是，Batch Normalization 和 pca 加白化有點類似，結果都是可以零均值加上單位方差，可以使得數據弱相關，但是在深度神經網絡中，我們一般不要 pca 加白化，原因就是白化需要計算整個訓練集的協方差矩陣、求逆等操作，計算量很大，此外，反向傳播時，白化操作不一定可導。最后，再次強烈直接看 BN 的相關論文，有很多細節值得一看！

編輯：hfy