什么是牛頓-拉夫遜方法?
牛頓其人:Isaac Newton(1642年12月25日– 1727年3月20日)是一位英國數學家,物理學家,天文學家,神學家和作家,被公認為有史以來最有影響力的科學家之一,并且是科學革命的關鍵人物。他的書《自然哲學的數學原理》于1687年首次出版,奠定了古典力學的基礎。牛頓還為光學做出了開創性的貢獻,并與戈特弗里德·威廉·萊布尼茲(Gottfried Wilhelm Leibniz)發展了無窮微積分的學科。
牛頓
拉弗森Joseph Raphson 生卒不詳,其最著名的著作是1690年出版的《通用分析方程》。它包含一種方法,現在稱其為牛頓-拉夫森方法,用于近似方程式的求根。艾薩克·牛頓(Isaac Newton)在1671年寫的《通量法》中開發了一個非常相似的公式,但是這項工作要到1736年才出版,這是拉夫森分析之后近50年。但是,該方法的Raphson版本比Newton方法更簡單,因此通常被認為是更好的方法。
所以,牛頓迭代法(簡寫)就是一種近似求解實數域與復數域求解方程的數學方法。那么這個方法是具體是什么原理呢?
牛頓迭代如何迭代?
直接看數學公式描述如何迭代不直觀,先來看動圖就很容易理解牛頓迭代法為什么叫迭代法以及怎樣迭代的:
牛頓迭代法是原理是根據一個初始點在該點做切線,切線與X軸相交得出下一個迭代點的坐標,再在處做切線,依次類推,直到求得滿足精度的近似解為止。
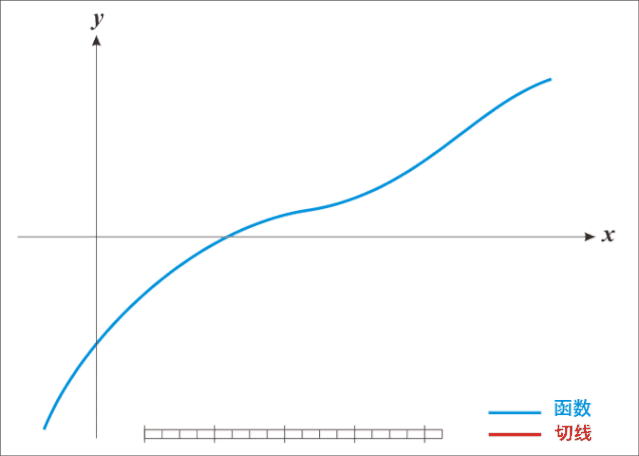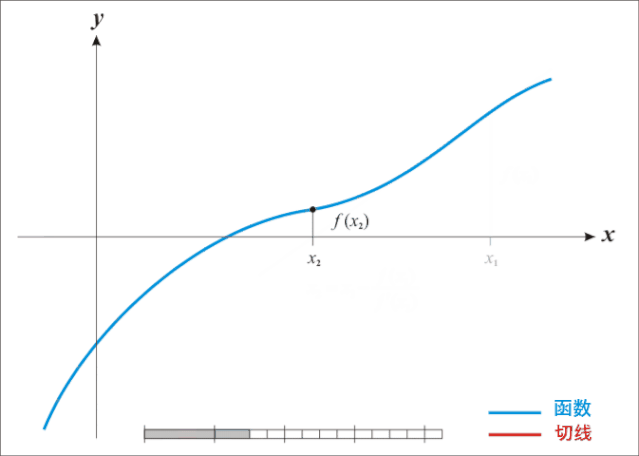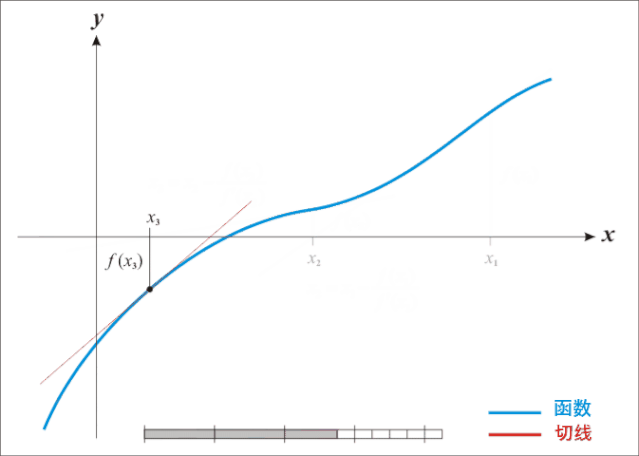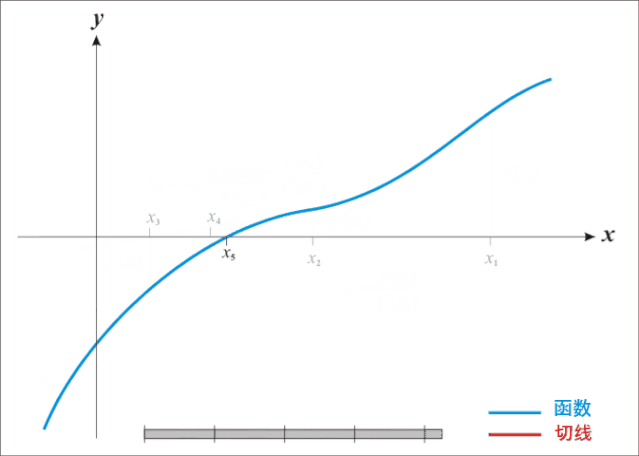
由前面描述知道,牛頓迭代法是用來近似求解方程的,這里有兩個點需要說明:
為啥要近似求解?很多方程可能無法直接求取其解
迭代法非常適合計算機編程實現,實際上計算機編程對于牛頓迭代法廣為應用
來看看,數學上如何描述的? 其中為函數在處的一階導數,也就是該點的切線。 來簡單推一推上面公式的由來,直線函數方程為: 知道一個直線的一個坐標點以及斜率則該直線的方程就很容易可以得知:那么該直線與軸的交點,就是也即等式的解:
啥時候停止迭代呢?
計算出
給出一個初始假定根值,利用上面迭代式子進行迭代
計算絕對相對迭代近似誤差
將絕對相對近似誤差與預定的相對誤差容限進行比較。如果,則迭代步驟2,否則停止算法。另外,檢查迭代次數是否已超過允許的最大迭代次數。如果是這樣,則需要終止算法并退出。另一個終止條件是:
如何編碼呢?
由于牛頓迭代法主要目的是解方程,當然也有可能用于某一個數學函數求極值,所以無法寫出通用的代碼,這里僅僅給出一個編代碼的思路。相信掌握了思路,對于各種實際應用應該能很快的寫出符合實際應用的代碼。 假定一函數為 其波形圖如下:
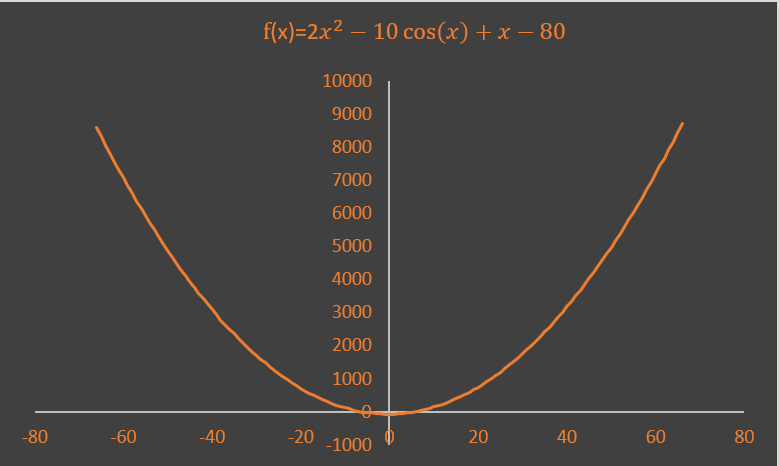
其一階導數為: 那么對于該函數的根: 從圖上大致可以知道有兩個根,如果直接解方程,則很難求出其根,可以編個代碼試試:
#include
需要注意些啥?
求斜率可能為0,如為0時,則可能找到了函數的極值,比如:
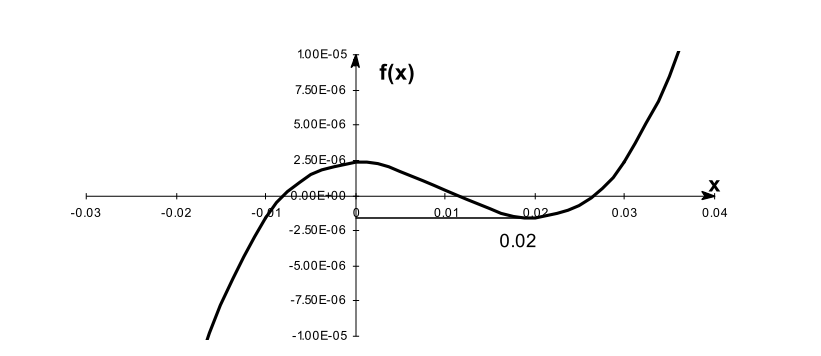
如果選擇的初始猜測根的接近方程f(x)=0中函數f(x)的拐點 ,Newton-Raphson方法可能開始偏離根。然后,它可能會又收斂回到根。例如:

5435866
如果選擇的初值不合適,可能會跳掉一些根,比如:

所以實際應用時,需要知道自己待求解模型的大致情況,在合理的加以調整。
有哪些應用?
比如知道某系統的傳遞函數,求解傳函的參數,可以將上述方法推而廣之,求解多維變量方程組,求導就變成求偏導了
又比如設計一電路測量某物質的阻抗
總結一下
牛頓迭代法在解決實際問題時,利用迭代求方程近似根的數學原理,在工程中有著很好的實用價值。比如求一個趨勢的極值,傳遞函數參數辨識等都有廣泛的實際應用。本文拋磚引玉,有可能文章也有很多錯誤疏漏的地方,如有不同看法或者發現錯誤,歡迎留言交流指正。
責任編輯人:CC
-
迭代法
+關注
關注
0文章
4瀏覽量
6270
原文標題:數學之美:牛頓-拉夫遜迭代法原理及其實現
文章出處:【微信號:elecfans,微信公眾號:電子發燒友網】歡迎添加關注!文章轉載請注明出處。
發布評論請先 登錄
相關推薦
SSM框架的源碼解析與理解
防水測試儀的多樣化測試方法:浸水法與氣壓法的深度解析

miniled 技術原理解析 miniled與 OLED 比較
汽車制動系統原理解析 如何檢查汽車制動系統
三種常見平方根算法的電路設計及Verilog實現與仿真
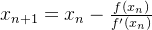
GRAEFF(格拉夫)順利通過UKCA(英標體系)認證
自然語言列舉法描述法各自的特點
【《計算》閱讀體驗】+徜徉于歷史人物事件中-跑跑計算實例感嘆于前人的智慧
巖土工程監測儀器之一:振弦采集儀的工作原理解析





 牛頓拉夫遜迭代法的原理解析
牛頓拉夫遜迭代法的原理解析











評論