經過一周的綜述撰寫,深感點云算法應用之浩瀚,只能仰仗前輩們的文章作一些整理:
點云硬件:
點云獲取技術可分為接觸式掃描儀、激光雷達、結構光、三角測距(Triangulation)、以及立體視覺等多種。最近二十年,點云獲取設備有突飛猛進發展。
經過20多年的發展,三維激光掃描硬件在穩定性、精度、易操作性等方面取得了長足的進步,尤其在機載/車載/地面三維激光掃描方面進展顯著,其中具有代表性的三維激光掃描硬件研制廠商包括:Riegl、Leica、Optech、Velodyne、北科測繪、海達數云等。此外還有美國NASA的ICESat和中國資源三號02星搭載的激光雷達。
點云軟件:
目前,工業界和學術界已經開發了多種針對點云處理的商用軟件和開源軟件。商業化的軟件主要有TerraSolid公司的TerraSolid(基于Microstation平臺開發,功能強大)、Trimble公司的Realworks、Leica公司的Cyclone、Bentley公司的Pointtools、Orbit GT公司的Orbit Mobile Mapping等,以及國內科研院所和公司開發的一些工具軟件,如武漢天擎的LiDAR Suite、西安煤航的LiDAR-DP以及北京數字綠土的LiDAR 360等。其重點主要集中在點云數據的管理、面向DEM生產的濾波[1]、三維建筑物提取及重建[2]、森林垂直結果參數提取[3]等方面。
此外,還有一些開源、自由的點云數據處理軟件,包括以下幾款:
Lastools:國際知名度高,C++編寫,分模塊,部分模塊開源,底層IO庫,壓縮庫都開源。
OPALS:維也納技術大學攝影測量研究組開發的軟件,學界最好。同樣是底層庫+功能模塊的結構,可支持幾乎任何一種激光雷達數據,處理效率很高。支持C++/Python二次開發。
BCAL LiDAR tools:一個ENVI插件,支持LiDAR格式點云的可視化、處理,IDL編寫。
CloudCompare:C ++開發,依賴于QT和OPENGL。支持基于插件的擴展機制。可拔插操作,可二次開發與源程序互不影響。富有活力,經常更新。
FUSION:開源軟件,功能很多,在forestry和ecology學界比較有名,可以計算多種LiDAR metrics。
相對三維激光掃描硬件設備的快速發展而言,三維點云的智能化處理發展較為落后,點云處理的智能化水平、軟件界面友好性、專業化應用數據接口方面還有待提高。
點云算法:
點云處理可以分為低中高三個層次。低層次處理主要包括濾波以及關鍵點的檢測;中層次處理包括點云的特征描述和分割、分類;高層次處理有配準、SLAM圖優化、三維重建等。與傳統的測量方式相比,三維激光掃描數據采集速度快、采樣頻率高,但也導致點云數據具有高冗余、誤差分布非線性、不完整等特點,給海量三維點云的智能化處理帶來了極大的困難。
濾波:
常用的濾波方法主要有直通濾波、體素法濾波、統計濾波、半徑濾波、條件濾波、雙邊濾波、高斯濾波、隨機采樣一致性濾波以及基于頻率的濾波。
除了以上比較常見的濾波算法,從LiDAR點云中去除地物點而保留地形點是點云濾波的一個重要環節。發展至今,算法可以歸為以下幾大類:
⑴布料模擬濾波
布料模擬濾波(Cloth Simulation Filtering,CSF)是一種物理模擬算法。該算法先將地表點云翻轉,然后讓一塊由格網構成的虛擬布料放置于翻轉后的點云表面最高處,使其自由落下,布料節點在重力和鄰近節點相互作用力的影響下會產生位移,會貼附于地形表面上。運算完成后,當布料上某節點的高程小于或等于對應點的高程,則將用點云的高程為該節點賦值,并將其標記為不可移動點。最后,計算密集匹配點云與布料節點的高差,大于閾值的被視為非地面點高差,反之則被視為地面點[5-6]。
⑵基于坡度的濾波算法
Vosselman[7]提出地面點間坡度值較小,計算各個點與周圍鄰近點間的坡度值,根據閾值可以判斷是否為地面點;Sithole[8]坡度閾值不再是固定常量,根據地形坡度的變化而變化;張皓[9]等采用坡度、坡度增量、最小坡度、最大坡度四個參數共同進行濾波判斷。
問題:計算量大、占內存;依賴閾值。
⑶基于形態學的濾波算法
形態學濾波原理:非地面點在形態學開運算前后高程變化較大,而地面點在形態學開運算前后高程變化小,通過設定閾值可將非地面點剔除(形態學腐蝕再膨脹)。
關鍵在于濾波窗口的選擇,Zhang[10]提出經典的漸進式形態學濾波,窗口有小變大,對應不同的高度閾值;此后學者在該方法基礎上進行改進,Hui[11]等結合克里金插值計算各層級局部區域的地形起伏度,以此為濾波準則進行優化。
問題:濾波窗口不好選取,漸進變化窗口效果不錯,但大窗口易將地形起伏點誤判為地物點。
⑷基于曲面擬合的濾波算法
原理:通常采用一定的插值擬合方法建立一個粗糙地形曲面,設定濾波準則,如點到曲面的距離,將不滿足條件的點逐步剔除。持續迭代,直到所有的地形曲面的精度達到所需的分辨率。
Kraus和Pfeifer[12]采用線性預測的方法,設定權重函數,在森林區域效果良好;Mongus和Zalik[13]提出了一種無參數的多層級漸進加密點云濾波法;Hu[14]等同樣采用TPS插值法,但在各層級進行擬合曲面時,計算各層級局部區域的彎曲能量,實現濾波閾值的自動計算。
優缺點:不需要過多的參數設置,自適應能力強,但多層級迭代,每一層級的濾波結果都會受到上一層的影響,初始地面不準確,就會出現誤差的傳遞與累積。內插方法也有很大影響。
⑸基于不規則三角網的濾波算法
原理:利用TIN模型中的地物臨近點云高程突變關系,研究利用高差臨界值條件和滿足該條件的臨近點數量等參數來過濾地物點。
Axelsson[15]提出經典的漸進加密不規則三角網(PTIND)濾波算法,簡稱PTD算法:首先獲取地面種子點,建TIN并進行迭代加密。在每次迭代過程中,都對其余各點到所在三角形的反復角和反復距離進行閾值判斷,滿足條件的點加入TIN,迭代至無點。Zhang和Lin[16]將光滑約束分割法與PTD方法相結合,減少地形凸起區域的細節誤差。隋立春[17]等首先對各個格網內的點云按升序進行排序,然后按照排序順序再對TIN進行加密,有效減小Ⅱ類誤差;吳芳等[18]在選擇地面種子點之前首先去除非地面點的影響,保證契合原有地形。
漸進加密不規則三角網算法近年來表現最為穩健。在復雜地形中效果良好,誤差低;但處理時間稍長,初始TIN對后續濾波影響很大;PTD算法對低位噪聲敏感,極易將低位噪聲點或低勢地物點誤判為地面點。
⑹基于分割的濾波算法
通常包含兩步,一是采取某種分割方法對點云進行分割,二是基于分割結果按照某種設定的規則進行點云濾波。
點云聚類分割的方法有很多:掃描線、Mean Shift分割法、區域生長法、、隨機抽樣一致等。濾波判斷的標準大多為地面點聚類區域低于地物點聚類區域。Lin和Zhang[19]首先采用區域生長法將點云分割成不同的部分,再設定規則選擇地面種子點,建TIN,PTD算法迭代;Tovari和Pfeifer[20]首先對點云進行分割,對分割后的每一部分計算殘差值,并根據殘差值對屬于同一部分的點云設置相同的權重,再按照Kraus和Pfeifer提的方法進行迭代濾波。
優缺點:能獲得更好的點云濾波效果,原因在于點云聚類分割,點云塊能夠提供更多的語義信息,更有利于后續的濾波判斷;分割后的點云能準確地到達地形斷裂線或者高程跳躍邊緣。但過分依賴聚類分割的結果。
⑺基于機器學習的濾波算法
基于機器學習的濾波算法將點云濾波視為二分類問題。采用某種機器學習算法,如條件隨機場、支持向量機、Adaboost等對訓練樣本進行訓練獲取訓練模型,然后采用此訓練模型對點云進行0(地面點),1(非地面點)標記。
Lu等[21]建立了一種基于離散和連續隱含隨機變量的條件隨機場模型,以區分地面點和非地面點;Jahromi等[22]提出了一種基于人工神經網絡(ANN)的算法:分別采用半自動化獲取訓練樣本和人工獲取訓練樣本兩種策略。Hu和Yuan[23]采用卷積神經網絡(CNN)通過對點云進行深度學習實現濾波,該方法將點云濾波問題轉化為圖像的分類問題,通過對1.728*10的7次方個標記的點云進行訓練學習,可以獲得1.5*10的八次方個參數的深度卷積神經網絡模型,現有濾波算法中精度最高。
缺點:需要大量的標記點云作為訓練樣本,耗費大量人力,占用大量計算機資源,耗時;訓練樣本要求覆蓋所有地形特征,很難實現。
⑻基于偽掃描線的濾波算法
偽掃描線:指將水平面上二維離散分布的激光點重新組織成一堆線狀連續分布點序列的一種數據結構。基本思想:兩點之間的高度差是由自然地形的起伏和地物的高度共同引起的。若兩個鄰近點之間的高度差越大,那么這個高度差是由自然地形引起的可能性就越小,更有可能是較高點位于地物上而較低點位于地面上。
優點:算法簡單,有效減少計算量并且保證了準確性,同時只需兩個濾波參數,較容易實現自動化;總能保證每個濾波窗口都包含有地面點,準確地提取出地形點;在平坦區域,效果非常好,在地形陡峭地區,誤差控制在較小范圍。
缺點:當地面點較少的時候,這類方法會失效;濾波窗口大小的選取還不能完全自動化,尤其在高程變化劇烈的區域和城市地區。
⑼基于多分辨率方向預測的濾波算法
方向預測法的思想:對于某一距離范圍,若當前點與所有方向預測值的差值均大于該距離條件下的最大高差限差,則該點為地物點,否則為地面點。
優缺點:此算法可以實現復雜尺寸的地物目標的剔除處理,由于數據集再數據量上的減少,地面點提取的效率有很大提高。對于附屬在斜坡上的建筑物會出現濾除不完全的情況,需要結合航片等輔助數據源來提高濾波精度。多分辨率平滑處理可以得到格網數據集,但格網之間存在縫隙,降低了精度,需要利用點云數據和格網數據集進一步做點云濾波處理。
⑽小結
總體而言,在訓練樣本足夠多的情況下基于深度學習的點云濾波算法能獲得最好的濾波效果,但其較為復雜的樣本標記和較長的處理時間會限制算法進一步發展;相較而言,基于分割的濾波算法因為能獲得更多聚類后的語義信息可以獲得更高的濾波精度,此外漸進迭代方式的算法也有較好的結果。
關鍵點特征線提取
點云數據的幾何特征主要是指對反映被測物體三維形態和紋理特征有關鍵性影響的點、線、面。不同的對象需要的特征提取方式不同,即便是同一對象也需要依照不同需求提取不同的特征。
在點云特征提取方式上,現有算法可以分為基于全局特征的方法和基于局部特征的方法兩類,全局特征利用點云上所有點的信息構建特征描述子。然而由于復雜場景下的物體遮擋、數據分辨率變化、噪聲干擾、背景影響以及視點變化等,使得獲取的點云具有顯著的多樣性。這些多樣性使得局部特征比全局特征更加勝任現實世界中的點云表示。局部特征提取通常包括關鍵點檢測和局部特征描述兩個步驟,其構成了三維模型重建與目標識別的基礎和關鍵。
本節主要闡述關鍵點和特征線的提取算法。
3.2.1 點云的關鍵點提取算法
點是三維點云數據中最基本的幾何形狀的特征基元,將三維模型模型表面具有代表性和描述性的點集定義為特征點,例如邊界點、尖銳點,以及相鄰曲面的公共點。關鍵點的數量相比于原始點云或圖像的數據量減小很多,與局部特征描述子結合在一起,組成關鍵點描述子,常用來表示原始數據,而且不失代表性和描述性。
⑴ISS算法(Intrinsic Shape Signatures)
利用協方差矩陣建立模型:把pi和周圍點pj的坐標相減:本質上這生成了許多從pi->pj的向量,理想情況下pi的法線應該是垂直于這些向量的。利用奇異值分解求這些向量的空間,擬合出一個盡可能垂直的向量,作為法線的估計。
利用特征值之間關系來形容該點的特征程度。顯然這種情況下的特征值是有幾何意義的,特征值的大小實際上是橢球軸的長度。橢球的的形態則是對鄰近點分布狀態的抽象總結。試想,如果臨近點沿某個方向分布致密則該方向會作為橢球的第一主方向,稀疏的方向則是第二主方向,法線方向當然是極度稀疏(只有一層),那么則作為第三主方向。如果某個點恰好處于角點,則第一主特征值,第二主特征值,第三主特征值大小相差不會太大。如果點云沿著某方向致密,而垂直方向系數則有可能是邊界。總而言之,這種局部坐標系建模分析的方法是基于特征值分析的特征點提取。
⑵Trajkovic關鍵點檢測算法
角點的一個重要特征就是法線方向和周圍的點存在不同,而此算法的思想就是和相鄰點的法線方向進行對比,判定法線方向差異的閾值,最終決定某點是否是角點。并且需要注意的是,本方法所針對的點云應該只是有序點云。本方法的優點是快,缺點是對噪聲敏感。
⑶3DHarris算法
在二維中是取一個窗口,然后移動窗口:
1.兩個特征值都很大,則為角點(兩個響應方向)。
2.一個特征值很大,一個很小,則為邊緣(只有一個響應方向)。
3.兩個特征值都小,則為平原地區(響應都很微弱)。
在點云中是建立一個方塊體,以體內數量變化確定角點。如果在點云中存在一點p:
1、在p上建立一個局部坐標系:z方向是法線方向,x,y方向和z垂直。
2、在p上建立一個小正方體。
3、假設點云的密度是相同的,點云是一層蒙皮,不是實心的。
a、如果小正方體沿z方向移動,那小正方體里的點云數量應該不變。
b、如果小正方體位于邊緣上,則沿邊緣移動,點云數量幾乎不變,沿垂直邊緣方向移動,點云數量改變。
c、如果小正方體位于角點上,則兩個方向都會大幅改變點云數量。
⑷NARF算法
NARF全稱normal aligned radial feature(法線對齊的徑向特征)。是一種3D特征點檢測和描述算法。能提取到 borders points 和其對應的 shadow points,提取到的特征點都是位于物體的外輪廓(邊緣)上,更加具有穩定性和可重復性。對特征點Normal的估計只使用共面點,因而對Normal的估計更加穩定。所有操作都是基于2D的range image,計算量相比于直接操作點云要小。
對點云而言,場景的邊緣代表前景物體和背景物體的分界線。所以,點云的邊緣又分為三種:前景邊緣,背景邊緣,陰影邊緣。三維點云的邊緣有個很重要的特征,就是點a 和點b 如果在 rang Image 上是相鄰的,然而在三維距離上卻很遠,那么多半這里就有邊緣。
1.這個點在某個平面上,邊長為 s 的方窗沒有涉及到邊緣。
2.這個點恰好在某條邊緣上,邊長 s 的方窗一半在邊緣左邊,一半在右邊。
3.這個點恰好處于某個角點上,邊長 s 的方窗可能只有 1/4 與點處于同一個平面。
將該點與不同點距離進行排序,得到一系列的距離;若這個數列存在某個階躍跳動(可能會形成類似階躍信號),那么發生階躍的地方應該是有邊緣存在。
⑸SIFT3D算法
尺度不變特征轉換(Scale-invariant feature transform,SIFT)是David Lowe在1999年發表,2004年總結完善。該算法通過求一幅圖中的特征點(interest points,or corner points)及其有關scale和orientation的描述子得到特征并進行圖像特征點匹配。
首先構建尺度空間,目的是為了模擬圖像數據的多尺度特征;為了尋找尺度空間的極值點,每一個采樣點要和它所有的相鄰點比較,看其是否比它的圖像域和尺度域的相鄰點大或者小。中間的檢測點和它同尺度的8個相鄰點和上下相鄰尺度對應的9×2個點共26個點比較,以確保在尺度空間和二維圖像空間都檢測到極值點。一個點如果在尺度空間本層以及上下兩層的26個領域中是最大或最小值時,就認為該點是圖像在該尺度下的一個特征點;然后去除不好的特征點:本質上要去掉尺度空間局部曲率非常不對稱的像素;上一步中確定了每幅圖中的特征點,為每個特征點計算一個方向,依照這個方向做進一步的計算,利用關鍵點鄰域像素的梯度方向分布特性為每個關鍵點指定方向參數,使算子具備旋轉不變性。
3.2.2 點云的特征線提取算法
在特征線提取方面,大部分學者主要針對網格模型進行相關特征線提取方法的研究,對點云模型的特征線提取研究相對而言較少,主要原因在于點云數據量大,本身沒有自然拓撲連接關系,而且還可能存在噪聲、數據缺失等問題,所以在點云數據上提取特征線比較困難。但是,利用點云數據提取特征線,由于不需要重建網格數據,具有所需時間少,而且數據容易獲取的優勢。
目前,基于點云模型的特征線提取的方法可以分為基于幾何特征、基于協方差分析和基于投影映射的三類方法。
⑴基于幾何特征的方法
此方法是利用點云的幾何信息,比如法向量、曲率、Voronoi圖等來提取特征曲線。Demarsin[1]等首先利用法向量估計的而信息對點云數據進行分割,對于每個分割后的區域內的點集,利用最小生成樹的算法進行特征曲線的提取。Yang B[2]等提出的方法首先將根據曲率選擇視覺突出點進行聚類,并未每個點賦予權重,然后提出描述點云形狀特征的波峰線。劉倩[3]等提出的方法在高斯映射的基礎上,對曲率值進行分析,主要是用來提取模型中較為尖銳部分的特征曲線,對于模型中的一些細微特征沒有辦法識別出。Merigot[4]等通過計算本地 Voronoi 圖獲得鄰域信息,然后計算曲率,但是 Voronoi 圖容易受到噪聲點的影響。
⑵基于協方差分析的方法
基于協方差分析的方法是根據協方差矩陣的特征值,通過對特征值進行計算分析,可以用來表示模型局部曲面的彎曲程度。Gumhold等[5]對局部鄰域構建協方差矩陣,計算得到特征值,根據其比例關系,將特征點分為邊界點,棱點,角點,構建最小生成樹,提取出特征曲線。上述方法需要高質量的點云,而且對細微特征不敏感。Nie J[6-7]等首先利用 PCA 計算曲面變化度,并根據符號曲面變化度絕對值識別潛在特征點,對其進行分割, 然后根據曲面變化度與設置的距離權重不斷將邊界點進行細化,最終采用最小生成樹的算法將特征點進行連接,得到特征曲線。但該方法隨著噪聲程度增加,特征線易出現斷裂和缺損。
⑶基于投影映射的方法
基于投影映射的方法是經過擬合得到模型的局部曲面,并將特征點投影在該曲面上。Daniels[8]等利用魯棒移動最小二乘法,擬合每個點鄰域的曲面,再將特征點投影到不同曲面的交線上,以提取特征線。但是因為該方法是在移動最小二乘的基礎上實現的,算法運行的時間過長,代價略高。龐旭芳[9]等通過擬合局部二次曲面計算曲率,然后找到與特征點距離最短的潛在特征線,并把特征點投影在該條線上,得到增強后的特征點。這種方法可以提取到模型上平緩和細微的特征,但是最終得到的特征曲線中有部分特征線之間有裂縫。
點云特征描述
一個良好的特征描述子應能包含所在局部表面的主要形狀信息以提供足量的鑒別力。此外,一個良好的特征描述子還應對噪聲、遮擋、背景干擾、點密度變化以及視點變化等穩健。現有的局部特征描述算法可以分為基于點特性、基于直方圖以及基于變換的算法三類。
3.3.1 基于點特性的方法
這類方法直接采用關鍵點局部鄰域內部分或全部點上的幾何屬性集合對其局部鄰域進行描述[45]。
Stein和Medioni[1]采用關鍵點的測地鄰域點法向量分布構建splash特征描述子。給定關鍵點p,首先采用測地半徑r獲得網格上的一個環狀切線,進而采用點p處的曲面切平面及法向量n構建一個局部參考坐標框架(Local Reference Frame,LRF)。采用該LRF,將點p的法向量與環狀切線上點的法向量的關系(即角度距離)采用一個三維矢量進行表示。接著,采用直線段對該三維曲線進行擬合,并以三維直線段的曲率和扭轉角(torsion angle)構建特征描述子。實驗結果表明,該算法對噪聲穩健。
Chua和Jarvis[2]提出了point signature特征描述子。Sun和Abidi[3]受人類指紋的啟發,提出了一種 point’s fingerprint 特征描述子。給定關鍵點p,首先以與點 p的測地距離相同的點構成一個測地圓(geodesic circle),采用一系列不同的測地距離從而獲得一個測地圓集合。進而采用點p的法向量和切平面構建一個LRF,并將這一系列測地圓投影到切平面上以獲得一組二維等值線。采用這些二維等值線以及測地圓上的法向量和半徑變化量等構成特征描述子。Sun和Abidi認為該算法優于 point signature 和 spin image 特征,且其計算量相對較小。
Malassiotis和Strintzis[4]通過對關鍵點p的鄰域點散布矩陣進行特征值分解從而構建一個LRF,然后在z軸方向與點p距離為d的位置放置一個虛擬針孔相機。該相機朝向點p,且該相機坐標系的x軸和y軸分別與點p處局部參考坐標系的x軸和y軸對齊。進而將局部鄰域點投影到虛擬相機的成像平面并記錄這些點到成像平面的距離從而獲得 snapshot 特征描述子。snapshot 特征描述子對自遮擋穩健且易于計算,其獲得了比 spin image更好的成對點云配準結果。類似的,文獻[5]首先定義一個LRF并采用一個規則的柵格對局部表面進行擬合,并采用局部表面在該柵格上的深度值作為局部特征描述子。最后,采用主成分分析(Principle Component Analysis,PCA)對該特征描述子做進一步壓縮。
Castellani等[6]通過順時針地將關鍵點p的一環(1-ring)鄰域點連接起來,接著將二環及三環鄰域點連接,不斷重復該過程直到測地半徑達到閾值r為止,從而獲得關鍵點p周圍的一個順時針回形線。在該螺旋線上提取采樣點的顯著級別、最大曲率、最小曲率以及表面法向量變化量等屬性,進而采用離散時間隱馬爾科夫模型(Hidden Markov Model, HMM) 記錄該螺旋線上的信息,從而獲得 HMM 特征描述子。該 HMM 描述子對旋轉、非均勻采樣以及網格分辨率變化等十分穩健。實驗結果表明其匹配性能優于spin image和3D shapecontext 特征描述子。
Steder 等[7, 8]首先將關鍵點p的鄰域表面與該點的法向量對齊,然后采用一個星狀模式圖(star pattern)放置到該對齊的表面上。該星狀模式圖的每個束線即對應于Normal Aligned Radial Feature(NARF)特征描述子的一個值。NARF描述子記錄了每個束線上的點變化量。為使得該特征描述子具有對旋轉的不變性,該算法從特征描述子中提取一個唯一確定的方向并依據該方向對特征描述子進行移位操作。該 NARF 特征描述子的特征匹配性能優于spin image 特征描述子。
3.3.2 基于直方圖的方法
這類方法首先利用點云的某些信息(如點坐標、幾何屬性)定義直方圖的一個或多個維度,然后采用鄰域點的幾何或拓撲測量值(如點數、 網格面積)對直方圖中的相應單元格進行累加從而獲得直方圖統計以實現對局部表面的描述[9]。這類方法可進一步細分為基于空間分布直方圖、 基于幾何屬性直方圖以及基于方向梯度直方圖的方法。
⑴基于空間分布直方圖的方法
這類方法依據局部鄰域點的空間分布(如點坐標)獲取直方圖統計以實現局部表面描述。這類方法首先在關鍵點上定義一個局部參考坐標框架或參考坐標軸,然后在該坐標系下將三維鄰域空間劃分成多個單元格,通過統計每個單元格上的空間分布測量值(如點數、網格面積)獲得特征描述子。這類算法主要需解決兩個問題,一是如何構建 LRF,二是如何對鄰域空間進行劃分。
spin image特征描述子對剛性變換、 背景干擾以及遮擋穩健[10],且在點云配準、三維目標識別以及三維模型重建等多個場合得到了廣泛應用。spin image已成為了三維局部特征描述子評估的事實基準[11-15]。但是,spin image依然存在許多缺陷:首先,spin image 特征對數據分辨率變化和非均勻采樣敏感;其次,由于該特征的計算過程需要將三維點云投影到二維空間,因而維度信息的丟失使得其鑒別力有限。后續有大量算法對 spin image 特征描述子的各個方面進行改進,典型例子如基于面的spin image[16]、spin image signature[17]、多分辨率spin image[18]、球形spin image[19]、尺度不變spin image[20]、以及顏色spin image[21]。
Frome 等[22]將二維 shape context 特征描述子擴展到三維點云,從而獲得三維形狀上下文(3D Shape Context, 3DSC)特征描述子。該算法采用關鍵點 p 的法向量 n 作為局部參考坐標軸,并將球形鄰域空間劃分成一系列單元格。為獲得對旋轉的不變性, Tombari 等[23]對 3DSC 進行了改進,通過給每個關鍵點賦予一個可重復且唯一確定的 LRF 以獲得單值形狀上下文(Unique Shape Context, USC) 特征描述子。實驗結果表明, 相比于 3DSC, USC 對存儲的要求顯著降低,且特征匹配的性能有所提高。此外,Sukno 等[24]亦提出一種對水平面旋轉具有不變性的非對稱模式形狀上下文(Asymmetry Patterns Shape Context,APSC)。實驗結果表明 APSC 獲得了與 3DSC 相當的性能。對二維 shape context的另一種改進是內蘊形狀上下文(Intrinsic Shape Context, ISC)特征描述子, 該描述子具有對等距形變的不變性。
Mian 等[25]提出了一種 3D tensor 特征描述子。該算法首先選擇一對滿足特定幾何約束的點構建局部參考坐標系,進而在該坐標系下進行空間三維柵格劃分,并計算點云網格與每個柵格單元的相交面積從而得到 3D tensor 特征描述子。由于該算法采用表面面積而非點個數來獲得直方圖, 因此其對噪聲和分辨率變化較為穩健。實驗結果表明該算法優于 spin image,其缺陷之一在于 LRF 的構建過程涉及網格頂點對的組合爆炸問題,因此運算量較大。
Zhong[26]提出了一種內蘊形狀特征(Intrinsic Shape Signature, ISS)描述子。該算法首先對鄰域點的協方差矩陣進行特征值分解從而構建 LRF, 進而采用離散球面網格將球形鄰域空間劃分成均勻分布的柵格。通過統計每個柵格單元內的點密度加權和從而獲得 ISS 特征描述子。車輛識別實驗結果表明,該算法在存在噪聲、遮擋和背景干擾時的性能優于 spin image和3DSC。
⑵基于幾何屬性直方圖的方法
這類算法依據關鍵點局部鄰域的幾何屬性(如法向量及曲率)進行直方圖統計從而獲得特征描述子。
Yamany 和Farag[14]采用單形角近似估計自由形狀表面上的曲率,將關鍵點鄰域的單形角累加到一個二維直方圖中,從而得到 surface signature 特征描述子。實驗結果表明 surface signature 優于splash、 point signature 和 spin image 特征描述子。
Chen 和Bhanu[27]通過將關鍵點鄰域的點數累加到一個二維直方圖中從而獲得 Local Surface Patches(LSP)特征描述子。LSP 特征描述子直方圖的一維為鄰域點的形狀指數值, 另一維為關鍵點 p 法向量與鄰域點法向量的夾角。實驗結果表明 LSP 在三維目標識別應用中能獲得與 spin image 相當的性能,但 LSP 的計算效率更高。
Flint 等[28]通過將關鍵點鄰域的點數累加到由表面法向量夾角定義的一維直方圖中從而獲得 THRIFT 特征描述子。Flint 等在其后續工作[29]中對該算法進行了改進, 改進的算法采用關鍵點法向量與鄰域點法向量的夾角計算加權直方圖。實驗結果表明THRIFT 對噪聲和點密度變化較穩健。
Taati等[30]對點云上每個點q的鄰域點協方差矩陣進行主成分分析從而獲得該點的 LRF 及三個特征值。在此基礎上,利用每個點 q 的 LRF 和特征值獲得一系列位置屬性值、 方向屬性值和散布屬性值,進而采用特征選擇算法從這些屬性中選取部分屬性,并將關鍵點 p 的鄰域點屬性值累加到一個直方圖中,從而得到可變維度局部形狀描述子(Variable Dimensional Local Shape Descriptor,VD-LSD)。Taati 和Greenspan[31]亦給出了基于模型幾何形狀和傳感器特性實現最優特征描述子選擇的方法。實驗結果表明,VD-LSD 在多個數據集上的識別率優于 spin image特征描述子。
Rusu 等提出了一種用于局部表面描述的 Point Feature Histograms(PFH) 特征描述子。對于關鍵點 p 鄰域內的一個點對,首先計算其 Darboux 框架,進而采用文獻[32]的方法計算由法向量以及點對距離向量等得到的四個測量值。最后,將所有點對的測量值累加到一個長度為16的直方圖中,即得到 PFH 特征描述子。為提高 PFH 的計算效率, Rusu 等[33]僅將興趣點與其鄰域點之間(而非所有鄰域點對) 的四個測量值累加到一個直方圖中,從而得到 Simplified Point Feature Histogram(SPFH)。最后將關鍵點 p 的所有鄰域點 SPFH 進行加權求和得到 Fast Point Feature Histograms(FPFH) 特征描述子。FPFH 保留了 PFH 中的絕大部分鑒別信息,且其計算復雜度明顯降低。
Tombari 等[9]首先為關鍵點 p 構建一個 LRF, 進而在該坐標系下將球形鄰域空間進行柵格化以獲得多個三維柵格單元。在每個柵格單元上, 依據落入該單元的點的法向量與關鍵點法向量的夾角將這些點累加到一個直方圖中。最后,將所有柵格單元內的直方圖串聯起來以獲得總的 Signature of Histograms of Orientations(SHOT)特征。SHOT 特征描述性強,計算效率高,且對噪聲穩健。實驗結果表明在各種噪聲強度下的 SHOT 性能均優于 spin image 及 point signature 特征描述子。然而,該算法對數據分辨率變化較為敏感。此后,Tombari 等[34]結合形狀信息和顏色信息提出了Color-SHOT(CSHOT)特征描述子。實驗結果表明,將顏色(紋理)信息融合到幾何特征描述子中有利于進一步提高其性能。
⑶基于梯度方向直方圖的算法
這類方法依據關鍵點的鄰域點梯度方向構建直方圖從而獲得特征描述子。
Hua等[35]將三維點云網格映射到二維規范化域中,并將表面的平均曲率和保角因子投影到一個兩通道的形狀矢量圖像中。對于每個通道,采用與尺度不變特征變換(Scale Invariant Feature Transform, SIFT)類似的方法提取特征描述子。首先將每個二維平面劃分成 16個子區域,并在每個子區域中依據梯度方向獲得一個八單元的直方圖。最后,將兩個通道中的所有直方圖串聯起來便得到最終的描述子。實驗結果表明,該特征描述子較為穩健且可良好應用于點云匹配。
Zaharescu 等[36]首先在點云網格的頂點上定義一個標量函數 f 并計算該函數的梯度 ?f ,該標量函數可以為曲率、法向量、密度以及紋理(強度)等。進而在每個關鍵點 p 處計算一個 LRF并將梯度向量投影到該坐標系三個相互正交的平面上,并將每個平面劃分成四個子區域。在每個子區域中,依據梯度方向 ?f 構建一個八單元的直方圖。最后,將三個平面上所有子區域中得到的直方圖連接起來便得到最終的網格方向梯度直方圖(Mesh Histograms of Oriented Gradients,MeshHOG)特征描述子。MeshHOG 的有效性已通過剛性和非剛性物體的特征匹配得到驗證。但是,MeshHOG 并不能應用于存在較大形變的物體。
Hou 和Qin[37]首先在點云網格的每個點上定義一個標量函數 f 并計算其梯度?f。進而采用極坐標系 [d(q) , θ (q)] 對每個鄰域點q進行表示,其中 d(q) 為從點p 到 q 的測地距離,θ (q) 為在局部切平面上從點 q 到 p 的主方向的極坐標角。接著,將該二維參數化平面分成九個子區域,并在每個子區域中依據梯度 ?f 的方向構建一個八單元的直方圖。最后將九個子區域中得到的直方圖串聯起來便得到了最終的特征描述子。匹配結果表明,該方法能獲得比 MeshHOG更高的召回率和精度,且對存在較大等距形變的物體亦能得到較好的結果。
3.3.3 基于變換的方法
這類方法首先將點云從空間域變換到其它域(比如譜域),進而采用該變換域中的信息實現對關鍵點局部鄰域的描述。
Hu 和Hua[38]首先對局部表面點進行Laplace-Beltrami 變換從而獲得局部表面的譜, 進而依據其譜分布構建直方圖作為特征描述子。實驗結果表明該特征描述子可很好地實現相似形狀的匹配。此外,該特征描述子亦對剛性變換、等距形變以及尺度變化等具有不變性。Sun 等[39]提出了一種熱核特征(Heat Kernel Signature,HKS)描述子。該算法將網格M當做一個黎曼流形,并將熱核 K t (p, q) 限制在時域,即 K t (p, p) 。K t (p, p) 即為所求的 HKS 特征描述子。該特征描述子可看做是多尺度的高斯曲率,其中時間參數 t 給出了尺度信息。HKS 是三維形狀的內蘊屬性, 其對等距形變具有較好的不變性。在后續研究中, Bronstein 和Kokkinos[40]提出了一種尺度不變 HKS 特征描述子用于非剛性形狀檢索,Kovnatsky等[41]提出了一種包含光度信息的 HKS 特征描述子。
Knopp等[42]將二維圖像中的加速穩健特征(Speeded Up Robust Feature,SURF)描述子推廣到三維點云領域,得到 3D SURF 描述子。該算法首先將點云體素化以得到三維體圖像, 并對該體圖像進行Haar小波變換,并采用關鍵點p鄰域的 Haar小波響應獲得關鍵點 p 的局部參考坐標系。接著,將關鍵點鄰域劃分成N b × N b × N b個單元,在每個單元中提取向量 v =( ∑ h x ,∑h y ,∑h z ) ,其中h x、h y和h z分別為沿 x、y和z軸的 Haar小波響應。最后,將 N b × N b × N b個單元中的所有向量串聯起來以獲得 3D SURF 描述子。
綜上所述,可得到如下簡要結論:
①在三大類局部特征描述算法中,基于直方圖的方法得到了最廣泛地研究。在基于直方圖的方法中,基于幾何屬性直方圖和基于梯度方向直方圖的方法均依賴于曲面的一階或者二階微分,因此這些方法對噪聲較為敏感。
②為獲得對剛性變換的不變性,大部分算法借助于 LRF 構建。這些算法首先在關鍵點上構建局部參考坐標系,進而將局部鄰域點轉換到該坐標系下。因此,LRF 的可重復性及穩健性對特征描述子的性能有很大的影響。
③為獲得對等距形變的不變性,部分算法采用測地距離(或其 k 環近似)代替歐氏距離,另有部分算法則通過將點云變換到某個特定的域中以獲得不變性,如 Laplace-Beltrami 譜域或時域。
④鄰域大小對特征描述子的性能有較大影響。一個大的鄰域半徑可使特征描述子記錄更多的形狀信息,但同時也使特征描述子對遮擋和背景干擾更加敏感。部分算法為其特征描述子配置了相應的自適應關鍵點檢測子。但事實上,可將任意兩個關鍵點檢測子和局部特征描述子進行搭配以尋找具有最優性能的組合。
⑤現有特征描述子難以同時獲得高鑒別力、對噪聲/數據分辨率/逸出噪聲等干擾的強穩健性以及高計算效率。
點云分割與分類
點云分割與分類識別是三維目標檢測的基礎,也是目前的研究熱點。三維點云分割是分類識別的基礎。點云的分割與分類有一定區別,點云分割是根據空間,幾何和紋理等特征點進行劃分,使同一劃分內的點云擁有相似的特征。點云分割的目的是分塊,從而便于單獨處理。點云的分類是為每個點分配一個語義標記,將點云分類到不同的點云集,同一個點云集具有相似或相同的屬性,如法向量、曲率、樹木、人等。
3.4.1 點云分割
三維點云的分割方法有很多種,一般主要有四種:基于邊緣、區域增長、聚類、顏
色RGB值的分割方法,以下分別介紹。
⑴基于邊緣的分割方法
Milroy[1]提出了一種新的確定邊界方式,即首先確定邊界點然后用能量等高線將各適界點連接起來即為邊界,其中將正交截面模型中曲率最大值點作為邊界點。劉勝蘭[2]提出了利用三角網格模型中主方向上主曲率為極值的頂點為特征點并且以此為起點做出特征線的提取方法。張強[3]將局部臨近點網格化,先將三角面片頂點的法向量調整為同一個方向,點的法向量是用加權平均相鄰三角面片的法向量替代的,然后利用平面點云的同向性和共面性對點云數進行分割。龔友平通過估算曲率的極值尋找邊界點,把邊界點連線從而構建邊界。Woo[4]使用八叉樹對空間網格進行細分和法矢標準差的提取,實現了三維點云的分割。
基于邊緣的分割方法速度快,對尖銳的邊界比較敏感,但確定邊界僅使用局部數據,所對于散亂的三維點云不能準確找到其邊界,分割結果達不到一定標準。
⑵基于區域增長的分割方法
該種分割方法實質是把相同特征的點劃分為一個區域,而區域主要通過自上而下、自下而上兩種方式不斷迭代增長。自上而下方法是先選擇種子片面或種子點,并且按一定準則向外延伸,確定鄰近點是否在相同面,持續到鄰域巧不存在連續點集,形成連接集合。而自下而上方法是先假設所有的點都在同一個面,擬合過程中誤差不符合要求時,就把原集合分為兩個集合。Kuo[5]等提出的DBRB(Delaunay-based Region-growing Algorithm)算法,該算法同時有Delaunay和區域增長的優點,先利用Delaunay構建三角片,角片為種子,不斷擴大,其實質是通過迭代不斷擴大三角片區域直到區域的邊界。梁學章[6]等提出一種三角網絡曲面的區域增長算法,先對點云進行預處理以達到數據精簡的目的,然后在點云中選擇新的匹配點構成新的三角形并連續更新邊界以達到分割區域的不斷增長。
基于區域增長的分割方法對由多項式表達的二次曲面分割更加有效。但在使用基于區域增長的分割方法時,由于需要選擇種子點或者種子片面,很難選擇合適的種子,并且很難區分光滑邊界,而且由于很難選擇合適的生長準則,受給定閥值影響大。其中自上而下的方法比較適用規則曲面的區域分割,自上而下的方法適用于數據點較少的。由于三維點云,往往場景很大,比較復雜,所以基于區域增長的分割方法適用情況有限。
⑶基于聚類的分割方法
該種分割方法屬于多元統計分析,根據樣本空間的特征,按照相似性和相似性測量準則對數據進行分類,使得同一類中的點有相同或者近似的屬性,不同類別的點的屬性不同。基于聚類的分割方法中常用的算法有:k-means算法,k-medoids算法,OPTIC算法,DENCLUE算法,STING算法,WAVE-CLUSTER算法,模糊聚類FCM。郭瑞[7]提出一種基于點的鄰域信息(灰度值、鄰域均方差、鄰域均值、B值、熵值)的FCM分割算法。針對漸進式聚類,時收斂速度加快,抗噪性增強。Jean Koh[8]利用數據點的特征權值構成八維特征向量,其包括:數據點的坐標、法矢量、高斯曲率和平均曲率,利用多層自組織特征映射網絡SOFM對八維特征向量來聚類,達到了區域分割的目的。劉雪梅[9]則添加法矢量、平均曲率以及高斯曲率來構成八維向量作為特征向量。
對于具有明顯的曲面類型的數據進行分割,基于聚類的分割方法效果比較好,然而對于復雜環境和結構復雜的物體中,很難直接確定曲面的分類個數和曲面類型。
⑷基于顏色RGB值的分割方法
為了豐富分割方法,提高分割品質,萬燕[10]等提出了一種基于HSV顏色空間的區域增長算法。該算法先求得區域增長的種子點同時確定分割的閾值,然后利用網格信息找到種子點的鄰近點集,最后根據H分量的相似程度分割點云。Zhuo[11]提出了一個無監督分割算法平衡RGB-D圖像中顏色和深度特性。輸出部分包含可大可小的分割部分正確地表示了實物在場景中的位置,并且時間小于監督分割算法。Steven Hickson[12]提出一種無監督分層的分割算法,該算法對深度和顏色的結合體進行過分割,再用一棵樹去合并過分割的區域。該方法準確地分割,并且質量得到一定提高。盧良鋒[13]將深度學習和RGB、深度進行有效的結合,該方法提離了物體的識別準確率。
3.4.2 點云分類
依據獲取特征的方式不同,本文將三維點云分類方法分為三大類:基于點的分類,基于傳統機器學習方法的分類和基于深度學習的分類,并對各方法進行了詳細地總結。
⑴基于點的分類方法
點簽名法[14](Point Signature),由 Chua 等人于 1994年提出。該方法根據每個點的球半徑鄰域與物體的交線 C 所擬合平面的法向量與參考矢量定義旋轉角,從而計算簽名距離,即每個點的簽名,通過匹配簽名實現分類。該方法消除了一階導數的計算過程,但對噪聲數據的處理效果較差。也有一些學者利用形狀特征對點云進行識別,如旋轉圖像[15-16]和體素網格[17]。如文獻[15]中提出了一種旋轉圖像法,通過二維數據生成旋轉圖以表征三維點云,可用于多目標分類但對大范圍的遮擋物不能進行有效識別。董[17]等人提出了一種用于激光掃描數據的多目標的層次化提取方法。該算法:利用點云的多種特征,如顏色,激光反射強度,法向量,主方向等生成超級體素,然后利用體素特征快速實現小規模場景中的多目標點云的分割分類,但對于沒有樹冠的樹木以及被樹木遮擋的街燈仍出現誤識別問題。
⑵基于傳統機器學習的方法
利用機器學習方法進行點云分類,本質就是借助模型進行特征的自學習和分類,國內外很多學者貢獻了很多研究成果。常用的監督學習方法有:隨機森林[18],支持向量機(SVM)[19],馬爾可夫隨機場等。如孫[18]等人提出了一種隨機森林的城區機載點云識別方法,結合幾何,紋理,空間等特征用于城市地物分類,實驗結果表明通過自動篩選特征的方法略優于所有特征分類精度。文獻[19]中提出了一種基于特征圖像的 SVM建筑物立面的半自動提取方法。該方法利用三維數據生成二維特征圖像,再結合支持向量機與二維網格屬性對特征圖像進行特征提取以達到分類目標。雖然有效降低計算開銷,但只能提取一般建筑物,不適用于復雜場景的多目標物提取。
⑶基于深度學習的分類方法
盡管以上方法在一定程度上能實現分類任務,但是特征的簡單組合,淺層模型很難推廣到大型復雜三維場景中。隨著以深度學習為代表的人工智能的快速發展,國內外研究者們嘗試將深度學習算法用于距離影像的分類。針對原有網格表示方法提取的低級特征表示不足,泛化性能差,無法滿足應用需求。Qi[20]等人首次打破傳統,設計了一種名為 Point Net 的網絡,其基本思想直接對點云進行處理,使用對稱函數解決了點云的順序問題,整合單點特征以形成全局的點簽名,能有效處理室內場景中的 3D 物體分類,目標分割和語義場景分割任務。但是 Point Net 不能捕獲度量空間點的局部特征,限制了其識別細粒圖案的能力和復雜場景的泛化性能。
為了解決這個問題,設計了一種名為Point Net++[21]的分層神經網絡。該網絡步驟為:將點云分割成重疊的局部區域,從中分層提取局部幾何特征,以形成高層特征。實驗結果表明,取得了良好的性能。以上方法均未考慮點云顏色等信息,但Roman[22]等人提出了一種 Deep Kd- Networks, 該網絡可以將數據的顏色、反射光強度、法向量屬性作為輸入,利用 kd- tree 將點云結構化,學習樹中每個節點的權重,在 Model Net數據集的準確率高達 90.6%,但該網絡對噪聲和旋轉敏感,對每個點都需進行上采樣或下采樣操作,會帶來額外的計算開銷。基于以上研究進展,Li[23]等人提出了一種簡單通用的點云特征學習框架——Point CNN。它利用多層感知機從輸入點中學習一種變換陣,將無序點云轉換成有序點云,在 Model Net 上準確率為91.7%,但置換矩陣離預想相距甚遠,點云的順序問題仍是一個難題,同時該方法是針對單一點云模型進行分類,因此面向復雜場景的點云數據分類也是亟待解決的難點。
點云配準
由于三維掃描設備對物體的視野有一定的局限,或者物體本身的幾何形狀較為復雜,所以不可能在同一視點上獲得物體的所有數據信息。為了獲得被測物體的完整點云數據,要將不同視角獲得的面點云數據集成起來進行點云配準工作。點云配準的目的是尋找三維剛體變換,使在不同視角下獲取的點云數據的三維坐標能夠正確匹配和重疊。配準算法可分為成對點云配準和多視點云配準算法兩類[1]。
3.5.1 成對點云配準算法
成對點云配準算法包含粗配準和精配準兩個步驟,其中粗配準可進一步細分為基于關鍵點匹配的粗配準算法、基于線匹配的粗配準算法以及基于面匹配的粗配準算法三類。上述三類粗配準算法既可單獨使用,也可組合使用[2]。
⑴基于關鍵點匹配的粗配準算法
這類方法首先在兩幅點云上提取一系列關鍵點,并采用每個關鍵點上的鄰域信息提取局部特征,進而通過特征匹配獲得關鍵點對集合(point correspondences),最后利用該關鍵點對集合計算點云間的初始變換關系。Chua 和Jarvis[3]在點云上提取一系列關鍵點,并采用 point signature 特征對每個關鍵點的局部鄰域進行描述。首先將一幅點云上的一個特征與另一幅點云上的特征進行匹配以獲得一個關鍵點對,進而找到另外兩個滿足特定空間約束的關鍵點對。得到三個關鍵點對后便可計算兩幅點云之間的變換關系。
Johnson和Hebert[4]采用spin image對關鍵點局部鄰域進行描述,并采用最近鄰法獲得關鍵點對。該算法對特征對進行聚類并采用幾何一致性算法去除錯誤的關鍵點對,最后采用滿足幾何一致性的關鍵點對計算兩幅點云之間的剛性變換關系。
Yamany和Farag[5]采用 surface signatures 對關鍵點局部鄰域進行描述,并采用圖像模板匹配及歐氏距離計算獲得關鍵點對集合。事實上,每三個關鍵點對組合均可得到一個剛性變換關系。為此,該算法從關鍵點對集合中選擇一系列滿足幾何一致性約束的關鍵點對組合, 并依據組合內點對的空間距離對所有組合進行排序,最后對每個組合得到的剛性變換關系進行驗證。
Rusu等[6]采用 PFH 特征對關鍵點局部鄰域進行描述。匹配時,首先從待匹配點云中選擇兩個關鍵點,并分別找到其在庫點云中的 k 近鄰關鍵點。通過將待匹配點云上兩關鍵點之間距離與庫點云上兩候選對應點之間距離最小化以獲得精確的對應點。接著,繼續從待匹配點云中選擇新的關鍵點并重復上述過程以找到待匹配點云上所有關鍵點在庫點云上的精確對應點。最后采用得到的特征對應點對集合計算剛性變換關系。
Tombari 等[7]采用SHOT作為局部特征描述子并通過特征匹配獲得關鍵點對集合。得到關鍵點對集合后,采用絕對方向(absolute orientation)算法[8]和隨機采樣一致性(RANSAC)[9]算法計算點云之間的剛性變化關系。
⑵基于線匹配的粗配準算法
這類方法首先在點云上提取一系列線條,并利用線條對應關系計算點云之間的變換矩陣。這類方法可進一步細分為基于直線匹配的方法以及基于曲線匹配的方法兩類。
基于直線匹配的方法首先從點云中提取一系列直線段,進而通過直線段匹配計算剛性變換關系。這類算法通常適用于包含較多平面和直線的物體,如建筑物等。Stamos 和Leordeanu[10]首先從點云中提取一系列平面和直線段,進而利用直線段的長度以及平面面積等信息高效地獲得兩幅點云間的匹配線段對集合。由于線段端點的位置準確度不高,因此文中只采用線段的位置和方向計算變換關系。理論上只需兩對對應線段即可實現點云之間的變換關系計算,因此從匹配線段對集合中可以得到一系列變換關系。最后,以能使得平面數量最大化的變換關系作為兩幅點云之間的變換關系。實驗結果表明該算法可用于大數據量下的復雜形狀點云配準,但該算法對具有對稱形狀的場景點云配準依然存在困難。
Chao和Stamos[11]對文獻[10]的算法進行了改進,提出了一種更加高效且支持用戶交互的算法。該算法通過點云分割和對提取的線段及平面法向量進行聚類以得到每幅點云的三個主方向,從而為每幅點云構建一個局部坐標系。通過將兩幅點云的局部坐標系進行對齊從而可快速精確地獲得點云間的旋轉變換矩陣。進而通過對旋轉后的點云直線段進行匹配從而獲得候選平移向量,最后采用最近鄰分類器對候選平移向量進行聚類,從而將聚類中心作為點云間的平移向量。為了進一步消除對稱三維表面可能帶來的錯誤匹配,該算法引入了一個用戶交互接口,從而可對拼接結果進行判斷并校正。對大場景(建筑物)的配準結果表明該算法可以達到毫米級的配準精度。該算法的缺陷在于某些場景(比如自然場景) 下提取直線段可能存在困難。
Vanden Wyngaerd和Van Gool[12]將這類算法進一步推廣到基于曲線的情況,從而通過雙切線匹配實現自由形態目標點云的配準。雙切線是由雙切點并集構成的一對曲線,其可在對偶空間中獲得。當從對偶空間中獲得點云的所有雙切線之后,將兩幅點云之間的雙切線匹配。當得到一對雙切線匹配對后,便獲得了四個匹配點對(即對應于兩個雙切線線段的端點)。由這四對匹配點對從而可以計算兩幅點云之間的剛性變換關系,并將點云變換到統一坐標系下以獲得配準誤差,以取得最小誤差的剛性變換關系用于點云粗配準。文獻[12]認為,相對于基于關鍵點匹配的算法,此文的算法運算量更小且穩健性更強。其缺陷在于,對于某些形狀的物體,其點云上提取的雙切點較少,因而難以獲得較好的配準結果。
⑶基于面匹配的粗配準算法
這類算法通過將兩幅點云的表面進行匹配從而實現配準。
Chung 等[13]采用主成分分析法實現點云粗配準。該算法首先對每幅點云上的點坐標進行主成分分析,從而得到三個主方向。該算法認為,當兩幅點云的重疊區域較大時,二者的主方向會比較一致,因此可以通過將主方向對齊來實現點云的粗配準。該算法比基于關鍵點匹配和線匹配的算法更加快速。但該算法同樣存在很大的局限性。首先,點云上必須有較多的點;其次,該算法要求兩幅點云有較大的重疊面積;再次,該算法對存在對稱表面的點云效果很差。當主成分分析得到的兩個特征值相差不大時,主方向的順序會混淆,從而使得變換矩陣發生錯誤。
Chen 等[14]采用 RANSAC 算法實現點云粗配準。該算法首先在一幅點云上隨機選擇三個點,并計算每兩個點之間的距離。然后在另一幅點云上選擇滿足上述距離約束的三個潛在對應點,從而構成三個點對以得到一個潛在的變換關系。重復上述隨機采樣過程,從而可以得到一個變換關系集合。最后,以獲得點云對應點數最多的變換關系作為兩幅點云之間的剛性變換。該算法即使在存在大量逸出點時亦能獲得很好的性能。但是該算法只適用于點云中點數較少的情形,否則隨機采樣的窮舉過程會導致運算量急劇增加。文獻[15]對該算法做了進一步改進以提高運算效率。
Brunnstrom 和Stoddart[16]采用遺傳算法尋找對應點對從而實現點云配準。首先,利用點云上點之間的距離和夾角信息定義遺傳算法的擬合函數,進而確定遺傳算法的交叉概率和突變概率, 并采用遺傳算法不斷迭代直到滿足停止條件為止。遺傳算法停止時,使得擬合函數最大化的染色體中包含了所需要的點對應關系。然而,這些點對中包含部分錯誤點對, 因此需要依據點對質量選擇其中的部分點對計算點云之間的剛性變換關系。該算法能獲得很好的匹配結果,但是其運算量很大,因而難以應用于對計算時間要求較高的場合。
Tarel 等[17]首先采用擬合算法獲得點云的隱式多項式模型,進而通過多項式模型實現點云配準。該算法不需要計算點匹配或面匹配,因而計算時間較快。但該算法要求兩幅點云之間有很高的重合度(通常要求重合度大于 85%),因此算法難以推廣到實際應用中。
⑷成對點云精配準算法
精配準算法可分為直接配準法以及迭代配準法兩類,而目前主流的算法是迭代配準法。
最經典的精配準算法為 ICP 算法[18],該算法通過最小化點對(亦稱為最近點)之間的距離從而實現點云之間的精配準。對第一幅點云中的每一個點均尋找其在第二幅點云中的最近點,從而可獲得一個最近點對集合,進而計算點云間的變換關系使得最近點對的平均距離最小。重復上述過程,直到滿足收斂條件為止。該算法在存在高斯噪聲時亦可以取得很好的性能, 其不足之處在于非重疊區域會對匹配結果帶來比較大的影響。此外,當初始配準不準確時,ICP 精配準容易陷入局部極小值[19]。后續有大量算法對 ICP 的各個方面進行了改進,如文獻[20–23]對 ICP 的運算速度進行了提升,文獻[24, 25]結合幾何或顏色特征提高 ICP 算法精度,文獻[26–28]側重于提高算法對逸出點等干擾的穩健性,文獻[26]針對 ICP 算法的精度和穩健性等進行了一系列改進。
Chen 和Medioni[29]的算法過程與 ICP 類似,其不同之處在于通過最小化點與面之間的距離實現點云之間的精配準。該算法的最小化優化函數為第一幅點云中的點到第二幅點云上的平面的平均距離。對于第一幅點云中的任一點,首先計算該點的法向量與第二幅點云的交點,進而采用第一幅點云中的點與其在第二幅點云中交點的距離作為點到面之間的距離。該算法對非重疊區域更加穩健,且其達到收斂所需要的迭代次數更少,其缺陷在于點面距離的計算比較耗時。針對該算法的不足之處,后續有不少算法對其進行了改進[ 30, 31]。
Liu[32]將點云精配準的迭代過程建模成一個馬爾科夫鏈,其首先從用于馬爾科夫鏈的 Lyapunov 函數中推導了可用于描述熱力學系統成分長拖尾和短拖尾概率分布的熵, 并通過最大化該熵值估計點云間采用最近點準則構建的點對概率。將估計的點對概率嵌入到平均場模擬退火算法中以實現全局最優化,進而采用加權最小二乘法實現變換關系估計。其實驗結果表明該算法優于 ICP 算法以及遺傳算法,其缺陷在于配準過程耗時過長。
3.5.2 多視點云配準算法
多視點云配準算法包含粗配準和精配準兩個步驟, 其中粗配準可進一步細分為序貫粗配準算法和同步粗配準算法兩類。
⑴多視點云序貫粗配準算法
序貫粗配準算法首先將兩幅點云配準,進而將第三幅點云與之前已配準的點云進行配準, 重復上述過程直到所有的點云均被配準到一個統一的坐標系下,如文獻[33, 34]。由于這類算法每次只將兩幅點云進行處理,因此減少了配準操作所需的內存和計算負擔,且每次操作的計算量與待配準的點云總數無關。由于配準誤差的不斷傳播,因此簡單的序貫粗配準算法精度較差。
Turk和Levoy首先對物體自上而下掃描從而得到一個基準點云,該點云包含了物體各個方位角的信息。進而將在各個方位角上掃描得到的點云與該基準點云進行配準,從而實現多視點云的配準。該算法巧妙地將多視點云配準問題轉化為成對點云配準問題,但其對點云掃描視點有一定的約束,因而應用范圍受限[35]。
Masuda等[36]采用 ICP 算法依次將一幅輸入點云與模型點云配準,并依據輸入點云上的點到配準后模型點云的誤差,將輸入點云上的部分點加入到模型點云中,不斷重復上述過程從而實現多幅點云的配準。
⑵多視點云同步粗配準算法
同步粗配準算法同時實現所有點云之間的配準,從而使得總的誤差最小化,并使配準誤差均勻分布到各幅點云上,避免了誤差的積累。這類算法需要解決兩個問題:一是獲得點云鄰接關系,即一幅點云與哪些點云相鄰;二是計算鄰接點云間的剛性變換關系。
Huber和Hebert[37]首先采用基于spin image 特征的成對點云配準算法將所有點云進行配準,從而獲得一個模型圖。圖的頂點為點云,圖的邊為兩個頂點對應的點云間的剛性變換關系。進而在圖中計算具有姿態一致性和全局表面一致性的張樹,利用該張樹便可實現點云的多視配準。文獻[38-40]等采用類似的思路,分別采用基于LPHM、EM和SHOT 特征的算法實現兩兩點云對之間的配準,并構建能獲得最大對應點對數(或重疊面積)的張樹實現多視點云配準。由于這類算法需要對所有點云對進行配準,時間消耗較大,因而難以實現對大量點云的配準。
Mian等[41]提出了一種連接圖算法用于多視點云粗配準。該算法首先選擇一幅點云作為連接圖的根節點,并將其它點云與該節點上的點云進行配準,從而將能配準上的點云作為該節點的子節點加入到連接圖中。不斷重復上述過程, 直到所有點云均已加入到連接圖中, 或者沒有圖像能加入到連接圖為止,從而得到最終的連接圖。該算法采用tensor 特征實現成對點云的配準, 并對配準進行全局一致性驗證。此外,Mian等進一步提出了一種超圖算法。該算法首先采用前述連接圖算法構建多個子圖,最后將子圖連接起來構成超圖,從而實現多視點云粗配準。該算法的效率優于張樹算法。
Ter Haar和Veltkamp[42]提出了一種快速的多視點云配準算法。給定一幅點云,首先找到與其對應的左視點云、右視點云以及后視點云。進而對這四幅點云進行驗證,通過驗證的點云組合便可構成物體的一個非完整模型,并對該模型進行姿態歸一化。最后,將得到的多幅非完整模型對齊從而獲得完整三維模型。該算法可在無先驗知識的情況下快速實現多幅點云的配準,其效率明顯優于的張樹算法。該算法要求四幅點云構成的組合應能基本覆蓋物體的完整表面,否則難以實現精確的配準。此外,該算法要求點云均是在相似的姿態下獲得的。
⑶多視點云精配準算法
多視精配準算法的任務在于對多視粗配準結果做進一步優化以減少所有點云之間總的配準誤差,并將配準誤差均勻分布到各幅點云上。
Stoddart和Hilton[43]將所有點云對應點之間的歐氏距離加權平方和作為優化函數,并采用梯度下降法迭代求解最優的剛性變換關系。該算法將多視點云配準過程類比于多彈簧系統的平衡過程,將兩幅點云之間的對應點集當做一個彈簧,采用剛體力學對彈簧系統進行分析, 從而在系統平衡點位置和方向求解過程中實現了點云變換關系最優化。
Neugebauer[44]將成對點云配準算法擴展到多視點云配準。該算法將所有點云間點到切平面的平均距離作為優化函數,采用最小二乘法對剛性變換關系進行迭代優化,并采用多分辨率點云加速配準過程。在開始迭代時,采用分辨率最低的點云,隨著迭代次數的增加, 參與配準的點云分辨率不斷提高,從而在保證配準精度的同時提高運算效率。
Benjemaa和Schmitt[45]將ICP 算法從成對點云配準擴展到多視點云配準,采用單位四元數法實現多視點云的迭代配準。Williams 和Bennamoun[46]將文獻成對點云配準算法擴展到多視點云配準,其基本思路與文獻[45]類似,主要區別在于該算法采用正交矩陣而非單位四元數表示旋轉矩陣。Nishino和Ikeuchi[47]采用類似的思路,采用共軛梯度法及M-估計器提高算法效率和穩健性,同時在尋找對應點時加入激光反射強度信息以進一步提高算法精度。
Masuda[48]采用有向距離場(Signed Distance Field,SDF)表示點云,進而基于SDF采樣同時實現多視點云配準和融合。該算法首先將點云融合得到融合形狀,進而將點云與融合形狀配準。雖然開始時融合形狀并不精確,但通過迭代地融合和配準,可使最終的配準結果趨于準確。該算法的優化函數與變換矩陣、融合形狀以及權值相關,點云融合通過計算每個采樣點上的 SDF 均值實現,點云配準通過尋找使得優化函數最小化的變換矩陣實現。由于每幅點云均與融合形狀配準,因此配準過程不會帶來誤差積累。此外,由于每幅點云均為融合形狀的一部分,因此無需考慮點云之間的重疊區域大小。
激光SLAM
即時定位與地圖構建 ( SimultaneousLocalization and Mapping,SLAM) 技術,是指把機器人放在未知的環境中,從一個未知位置開始移動對環境進行增量式地圖創建,同時利用創建的地圖進行自主定位和導航。SLAM技術可以使機器人實現真正的自主導航。
SLAM是一個龐大且復雜的工程問題,不同的傳感器通常對應著不同的SLAM解決方案,例如,激光傳感器對應著激光SLAM,相機類傳感器對應著視覺SLAM。通過集成LiDAR掃描儀、IMU(inertial measurement unit)等傳感器可在掃描平臺移動過程中實時獲取位置、姿態信息以及場景的空間信息。基于SLAM技術的激光掃描可以高效完成室內空間或室外小場景的三維點云數據獲取。本節主要介紹激光SLAM。
3.6.1 激光雷達SLAM定位技術
常見的移動機器人領域定位有位姿跟蹤和全局定位兩種。位姿跟蹤是指機器人的當前位姿根據上一時刻的位姿進行遞推計算,要求機器人的初始位姿必須已知。全局定位是指機器人被放在任何環境的任意位置,不必已知初始位姿,根據傳感器信息獲取機器人在全局坐標系中的位置。
⑴掃描匹配法
掃描匹配算法是一種位姿跟蹤定位方法。根據是否依賴于掃描的初始估計,分為半自動掃描匹配和自動掃描匹配。半自動掃描匹配在位姿初始估計的基礎上迭代地使匹配更準確,但缺點是當初始估計不準或沒有初始值時可能會導致匹配失敗;自動匹配方法直接求解掃描的位姿,通常匹配的結果精度不高。常用的掃描匹配方法有:迭代最近點( Iterative Closest Points,ICP) 算法,隨機抽樣一致( Random Sample Consensus,RANSAC) 算法等。
ICP 算法通過迭代的方式找出兩個點集的空間位置變化關系,使對應點對的均方差最小化,實質是一種基于最小二乘法的最優匹配。這種采用最近鄰尋找對應點的傳統 ICP 方法,存在位姿中旋轉估計收斂慢的缺點。后來的研究者不斷將其改進,其中 IDC( Iterative Dual Correspondence) 和 MBICP( Metric-Based ICP) 兩種改進方法中分別引入新的點匹配策略進行了改進。PLICP ( ICP Based on Point-to-Line metric) 算法利用點到線段匹配的方法改善了迭代效率,但魯棒性變差,且更容易受到初始位姿誤差的影響。郭瑞提出了一種極坐標點匹配 規則 ( ICP Based on Polar Point Matching,PMICP) ,該規則綜合考慮了旋轉和平移的影響,并通過實驗數據驗證了該方法相對于傳統 ICP 算法及其改進算法的快速性、準確性及魯棒性,可以確保局部地圖緊密一致,但是該方法不能避免匹配誤差的累計,所以不能保 證全局地圖一致,而且PMICP 算法依賴于掃描間相對位姿的初始估計,僅適用于單步定位,也未考慮環境中的動態變化。因此研究者又提出了從掃描數據中提取的特征完成匹配,即基于幾何統計特征的自動掃描匹配方法( Automatic Scan Matching based on Geometric Statistic Features,GSF-ASM) ,該方法不需要位姿的初始估計,而是在迭代過程中逐漸找到好的對應點并逐漸校正位姿估計。此外,通過分割段特征和掃描點特征的匹配過程,過濾掉了環境變化的區域,更適應動態變換的環境。
隨機抽樣一致算法通過反復在一組數據中選擇隨機子集的方法,利用迭代方式估計數學模型的參數,能夠有效應對環境中的粗大誤差。隨機抽樣一致算法是一種不確定算法,對參數的選擇非常敏感,而且只是有一定的概率得到合理的解,因此為了提高精度需要以增加迭代次數為代價。Yang 等人提出了一種基于多模型的隨機抽樣一致算法,該算法中將模型分為靜態環境模型和動態目標模型等,用于在高動態環境中估計車輛的位置。
⑵擴展卡爾曼濾波( Extended Kalman Filter,EKF)定位
Smith 等人[1]在 1987 年提出基于卡爾曼濾波( Kalman Filter,KF) 的 SLAM 算法,卡爾曼濾波器是一種通過預測和校正過程對線性高斯系統的狀態進行估計的遞推算法,這是一種經典的位姿跟蹤算法。
由于卡爾曼濾波只對線性高斯系統有效,應用受到限制,研究者對其改進,提出擴展卡爾曼濾波器定位,應用 EKF 對機器人位置和路標位置進行同時估計,EKF 定位適用于非線性高斯系統。EKF方法將機器人的位姿和環境特征地圖用一個高維狀態向量表示,對輸入和輸出方程利用泰勒級數展開形式進行局部線性化,然后對狀態向量的均值和最小方差進行估計。EKF 算法能有效處理不確定信息,但在每次迭代過程中計算各個特征間的協方差矩陣,增大了算法復雜度。EKF 方法基于機器人位姿的不確定性為單模高斯分布假設,假設傳感器數據在機器人位置上映射為高斯形狀的分布,但由于復雜的實際環境無法滿足這種強假設,所以仍需要不斷的改進。
另一種基于卡爾曼濾波的優化方法是無損卡爾曼濾波器( Unscented Kalman Filter,UKF) 。UKF通過近似概率來實現非線性濾波,誤差比 EKF 更小。UKF 通過無跡變換( Unscented Transformation,UT) 將制定權值范圍內的粒子集合帶入所采用的非線性函數,進一步得到其統計特性。這樣使粒子向后驗概率高的區域變動,粒子可以更好的近似狀態變量的后驗概率密度函數。當計算量在可控的范圍內時,使用 UKF 得到的定位結果要比 EKF 得到的定位結果更好。
Shojaie 等人發現,迭代觀測更新過程能有效的減少線性化誤差,同時提高估計精度。由此提出了迭代擴展卡爾曼濾波器( Iterated EKF,IEKF) 、迭代無損卡爾曼濾波器 ( Iterated UKF,IUKF) 和迭代Sigma 點卡爾曼濾波器( Iterated Sigma Point Kalman Filter,ISPKF) 。
Thrun 等人提出一種基于協方差矩陣的逆來改正機器人位姿的方法。信息濾波 ( Information Filtering,IF) 是另一種針對卡爾曼濾波研究的改進。信息濾波是基于信息矩陣和信息向量的表示方法,本質是應用信息矩陣代替協方差矩陣表示不確定性,同時利用信息矩陣的稀疏性進行等時間間隔的執行預測和更新,有效地減少計算量。
⑶馬爾可夫定位
馬爾可夫定位[2]將定位問題視為一個離散的馬爾可夫過程,是一種成功的全局定位方法。基于馬爾可夫假設,即假設機器人觀測獨立和運動獨立,FOX 等人最先提出了馬爾可夫定位方法,計算機器人在所在全局環境的概率分布。馬爾可夫過程中的每一個狀態對應于機器人的每一個離散化的位姿,優點是能夠處理多模和非高斯的概率分布,有效解決位姿跟蹤和全局定位問題。馬爾可夫定位通用性較強,可用于任何環境的定位,但是其效率較差。根據地圖表示方法的不同,馬爾可夫定位方法可分為拓撲馬爾可夫定位 ( Topological Markov Localization,TML ) 和柵格馬爾可夫定位 ( Grid Markov Localization,GML) 。馬爾可夫定位方法最早應用在基于拓撲地圖的定位中。柵格馬爾可夫定位將連續的機器人位姿空間離散化為均勻的柵格,在柵格上完成數值積分。但由于計算量與狀態空間的尺寸和分辨率相關,這種方法計算量太大。
Burgard 使用八叉樹獲得狀態空間的變分辨率表示,使計算量和需要使用的內存空間得到縮減,解決了來自固定分辨率的限制。吳慶祥等對馬爾可夫定位進行了仿真研究,使用電子羅盤解決對稱環境中的定位問題。Konolige 等人提出基于傳感器數據和地圖相關性的馬 爾可夫定位方法( Correlation-based Markov Localization,CBML) ,減少了定位過程中的計算量,提高了地圖更新的效率。Kosechka 和 Li 基于機器視覺建立室內環境拓撲地圖。Gutmann 提出一種集成馬爾可夫定位和EKF 的定位方法 ML-EKF。
馬爾可夫是一種基于概率的全局狀態估計方法,通過傳感器對環境的測量和自身運動對機器人狀態進行遞歸的估計,以獲得最接近機器人真實位置的狀態。此外,馬爾可夫定位可解決在定位初期因初始位置未知和環境相似性造成的多峰值分布問題,并能從定位失敗中恢復。從運動控制的方面,馬爾可夫定位結果直接確定了機器人與環境的相對位置關系,例如距離,這也是大多數機器人系統的重要輸入信息。
⑷粒子濾波定位
Dellater[3]等人和Koller[4]等人提出了蒙特卡羅定位( Monte Carlo Localization,MCL) 方法,這是一種全局定位方法。蒙特卡羅定位是采樣/重要性重采樣 ( Sampling /Importance Re-sampling,SIR) 的一種版本,更為人們熟悉的叫法為粒子濾波( Particle Filter) 定位。粒子濾波的思想是用 N 個帶有權重的粒子來表示機器人位姿的后驗概率密度分布。根據系統狀態的條件概率分布在狀態空間構造一組隨機粒子,根據觀測信息不斷調整每個粒子的位姿和權值,根據調整后的粒子信息來校正系統狀態先前的條件概率分布。
粒子濾波器不受線性高斯系統的限制,可應用在任何非線性的隨機系統,但在全局定位中需要較多的粒子,而在位姿跟蹤中,即機器人的初始位姿已知時,只需要很少的粒子就能得到較好的定位效果。粒子濾波的最大問題是會出現由于重采樣過程而導致的粒子耗盡,這時粒子將沒有辦法逼近機器人位姿的真實后驗分布。Koller 和 Kwok 等在定位機器人的過程中自適應地調整樣本數量來降低計算量,Thrun 等提出 Mixture-MCL 算法,改變樣本的產生方式,在樣本數量較小的時候,使其產生良好的定位效果。Saarinne 等提出一種基于正態分布變化的蒙特卡洛定位方法 ( Normal Distributions Transform Monte-Carlo Localization,NDT-MCL ) ,用正態分布變化作為地圖和傳感器數據的表示形式,提高了室內機器人定位的精度和可重復性。
3.6.2 激光雷達SLAM地圖創建技術
地圖創建是指依靠移動機器人自身攜帶的傳感器,在移動過程中,根據自身傳感器不斷采集的位姿和環境信息數據,建立環境地圖的過程。首先機器人根據傳感器傳回的實時數據信息建立局部地圖,然后將局部地圖并入到全局地圖。每次得到的局部地圖既包含全局地圖已有的信息,也有全局地圖沒有的新的環境信息。在地圖創建過程中,不僅僅實現了對環境地圖的估計,同時還實現了對移動機器人位姿的估計,也再次說明了定位與建圖相輔相成的過程。地圖表示方法在前文已經說明,根據不同的地圖更新方式,不同的地圖創建方法有其各自的優缺點及其需要解決的主要問題。
⑴基于濾波的地圖創建算法
①基于EKF的地圖創建算法
EKF 方法是解決 SLAM 問題的一種經典方法,依賴于運動模型和觀測模型的高斯噪 聲假設。Smith 等人利用 EKF 方法提出的數學公式至今仍在廣泛使用。EKF-SLAM 采用增廣的系統狀態空間,濾波過程包括狀態預測、狀態更新和地圖更新,對增廣的系統狀態和增廣的系統協方差矩陣進行遞歸的更新替換。其中地圖更新部分,主要是在完成系統狀態更新后,機器人把當前時刻的位姿和環境特征狀態存儲到環境地圖中。地圖更新主要包括: 匹配成功的特征點更新、新特征的加入、擴展地圖、錯誤特征的刪除。由于 EKF 的限制性,隨后許多研究者對該方法進行了改進。EKF-SLAM 能夠以在線的方式估計地圖的全后驗概率,能夠獲得最可能的地圖和機器人位姿,地圖中維護的不確定性在機器人利用地圖導航的時候有極大的好處。此外,此框架能夠使機器人位姿和所創建的環境地圖依概率 1 收斂到真實值,其收斂程度由機器人初始不確定性和傳感器觀測的不確定性決定。基于EKF-SLAM 框架,研究人員在不同機器人系統上完成了很多開發工作。但是由于 EKF-SLAM 框架存在算法一致性限制、數據關聯限制、計算成本高的限制,因此這種框架只適合建立小規模地圖。研究者們不斷提出改進,如分割更新、稀疏信息濾波和子地圖方法等,一些研究者將掃描匹配放進了傳統的 EKF-SLAM 的框架內。
②基于RBPF的地圖創建算法
Rao-Blackwellized 粒子濾波器 (RBPF) 的基本思路是:在 RBPF 中每個粒子代表了一條可能的機器人估計和地圖,其關鍵任務是估計環境地圖 m 和機器人運動軌跡的聯合后驗分布。
RBPF 在特征地圖和柵格地圖的 SLAM 中應用都比較成功。相對于 EKF-SLAM,RBPF 對數據關聯不敏感,容許錯誤的數據關聯。即當發生數據關聯錯誤時,RBPF SLAM 比EKF-SLAM 效果好。RBPF SLAM 系列算法的主要問題是解決由于重采樣造成的粒子多樣性喪失,即粒子耗盡問題。Hahnel 等將 RBPF 和掃描匹配相結合,通過設計掃描匹配造成的誤差模型,使掃描匹配最小化航跡推測誤差,降低需要的粒子數。Grisetti 等對 Hahnel的算法進一步改進,通過同時考慮機器人運動模型和當前觀測的建議分布及采用自適應重采樣技術兩種方法來提高 RBPF性能。Blanco 等使用Kullback-Leibler Distance( KLD) 方法自適應確定粒子數量。朱磊等人將人工魚群算法引入,使粒子分布在重采樣之前就更加接近真實情況,隨后利用定向重采樣方法使新產生的粒子更加接近真實運動。
③基于 Fast SLAM 方法的地圖創建算法
Montemerlo 等[5-6]基于Rao-Blackwellized,提出了Fast SLAM算法。其實質是在RBPF-SLAM算法的框架內,加入了 EKF 對環境的特征地圖標識。基本思想是把機器人 SLAM 系統分解為位姿估計和環境地圖估計兩部分。其中位姿估計采用粒子濾波算法估計機器人路徑,環境地圖則采用擴展卡爾曼濾波器更新。但上述方法粒子退化現象嚴重,為了解決這個問題 Montemerlo 等人提出了Fast SLAM 2. 0 算法[7],進一步在重要性權值計算過程中引入高斯分布函數,有效的解決了粒子退化現象,提高了算法的精度和有效性。
⑵基于圖優化方法的地圖創建算法
Graph SLAM 由 Lu 和Milois[8]在1997年提出。Graph中的節點表示位姿,節點之間的邊表示由航跡推測得到的位姿間的約束。Graph SLAM 算法包括前端構圖和后端優化兩部分。前端構圖包括特征提取、數據關聯,后端圖優化常用方法有最小二乘法、隨機梯度下降法、松弛法和基于流行的圖優化等。Graph SLAM 將地圖創建視為最優化問題,首先定義目標函數和約束條件,然后用數學規劃方法求解。Graph SLAM 是在采集完所有傳感器數據后,在建立好所有約束條件的前提下進行離線位姿估計和地圖創建的。目前較著名的 Graph SLAM 算法有:PTAM-SLAM、LSD-SLAM、ORB-SLAM、SVO-SLAM 和 RGBD-SLAM 等。
⑶基于其他SLAM技術的地圖創建算法
Thrun 提出一種基于概率方法的期望最大化( Expectation Maximization,EM ) 算法。期 望( Expectation) 是基于當前相似性最大地圖來估計機器人的位姿;最大化( Maximization) 是基于期望步驟所得到的機器人位姿來估計相似性最大地圖。基于 EM 的 SLAM 方法,將地圖創建轉化為概率約束條件下的最大相似度估計問題,然后再估計機器人的位姿,這種方法具有很好的地圖創建和定位性能。但是它是一種非增量的分批算法,且不能實時運行。后來 Thrun 等結合 EM 算法和增量算法,提出了一種新的實時性算法,該算法主要計算機器人位姿的全后驗概率來確定最相似的位姿,但是由于后驗概率計算的時間復雜度高,這種算法不能用于大規模環境。
3.6.3 激光SLAM展望
隨著人工智能技術的發展,將來會考慮將智能化方法引入激光 SLAM 過程,如神經網絡模型、集元理論等在優化、分類和可靠性方法都具有優勢,這些算法的引入將會讓激光 SLAM 擁有更好的前景。另外,無人駕駛技術要求地圖高效、準確的反映動態環境信息,同時需要地圖與無人車之間擁有更好的交互性,而目前常見地圖表示方法不能滿足這樣的要求,因此研究更高效的適應室外非結構環境下的地圖表示方式,也是未來的發展方向。此外,基于多種傳感器融合技術和多車協作也是未來激光 SLAM 的發展方向。
隨著無人車技術的發展,目前激光 SLAM 技術是 SLAM 研究領域的熱點,也是無人車實現在 GPS信號失靈情況下進行自我定位的重要保證。由于激光的精度高、速度快及安全性高等特點,激光SLAM 在無人車、無人機和機器人自主導航等方面得到越來越廣泛的應用。在無人車技術領域,隨著激光 SLAM 技術的不斷探索和發展,未來的激光SLAM 技術將會擴展到動態、三維的非結構環境應用中去,以實現無人車的不依靠 GPS 的全自主導航。
點云三維重建
表面重建算法的任務在于從多幅點云中構建物體的統一曲面表示,下文將對幾種典型的表面重建算法進行評述。
3.7.1 網格縫合法
Boissanat[1]提出了一種用于實現三維點集 Delaunay三角化的算法,Rutishauser等[2]進一步利用該算法實現三維模型網格的生長。該算法通過在點云中尋找與現有模型網格邊緣較近且不重疊的點并將該點加入到模型網格中,從而實現模型網格的更新生長。
Turk 和Levoy[3]提出了一種網格縫合(mesh zippering)法。該算法將點云網格逐一進行縫合,從而得到反映物體完整三維形狀的粗模型,最后將所有點云網格與粗模型對齊并通過求均值以獲得更加精確的三維模型。對于配準的兩幅點云網格,首先沿著網格邊緣將重疊的區域刪除,進而對其中一幅點云網格的邊緣進行修剪以和另一幅網格良好吻合,并去除得到的小三角形。將所有點云網格縫合從而得到一個粗模型,進而在原始點云上尋找與粗模型上的點滿足幾何一致性的點,將這些點的坐標均值作為最終模型上相應點的坐標。該算法可在掃描的同時對點云逐個進行配準,因而可以減少存儲量。當點云網格的配準不精確或噪聲較大時,該算法的性能較差。此外,該算法得到的模型在縫合處有較明顯的接縫[4]。文獻[5]亦采用類似的方法實現三維表面重建。
3.7.2 隱函數法
這類算法通常構建一個隱函數對三維表面進行描述, 進而通過提取隱函數的等值面實現三維表面重建。
第一類方法是體素法。該方法在三維體數據中構建一個隱函數,并采用移動立方體(Marching Cubes, MC)算法從體數據中重建出隱函數為 0 的表面。這類算法不同變種間的差異主要體現在隱式曲面定義和體數據組織上[6],體素法在三維模型重建中得到了廣泛的應用。Curless 和Levoy[7]首先對點云進行體素化,并將每幅點云轉化為有向距離函數。進而將每個體素中來自多幅點云的有向距離函數加權求和,從而得到該體素對應的累積有向距離函數。接著,采用 MC 算法在體素柵格中提取累積有向距離函數等于 0 的等值面,從而實現三維模型重建。實驗結果表明,該算法可從大量點云中獲得無縫且細節豐富的高精度三維模型。文獻[8-10]采用類似的方法實現三維表面重建。Johnson 和Sing[6]則采用概率占據網格方法獲得體數據進而采用 MC 算法實現表面重建。該占據網格基于點的接近性以及傳感器誤差模型實現對三維表面的概率描述,因而可通過調整誤差模型使得算法適用于不同類型傳感器。
第二類方法是泊松法[11]。該算法為模型構建一個示性函數,該示性函數在模型的內部取值為1,在模型外部取值為 0。然后用示性函數的梯度場去逼近點云的法向量場,從而將示性函數的求解轉化為泊松函數的線性求解問題。采用最小二乘問題獲得示性函數的解后, 采用類似于 MC 算法的方法提取等值面從而實現三維表面的重建。該算法一次考慮所有采樣點,無需采用啟發式的空間分割或融合,因而對噪聲穩健。其次,該算法的隱函數梯度在所有空間點上都進行了限制,生成的錯誤面片較少,因而對散亂點云穩健。但該算法對無完整包絡的物體(如室外建筑物點云)重建效果較差。
3.7.3 轉球算法
Bernardini 等[12]提出了一種用于三維表面重建的轉球(ball-pivoting) 算法。該算法假設點云密集分布在整個曲面上從而使得半徑為 ρ 的球可以在該點云表面上滾動而不會掉到點云內部。在每次滾動時,均有三個采樣點支撐住該球。該算法首先選擇三個合適的點構成模型網格的種子三角形,該三角形的三個點均在半徑為 ρ 的球表面上。進而將該球繞三角形各邊旋轉直到接觸到新點為止。該旋轉邊與找到的新點一起便構成了一個新三角形, 并將該三角形加入到網格中。重復上述過程直到所有可旋轉的邊均已完成測試,則算法轉而尋找下一個種子三角形,直到將所有點遍歷完為止。為應對采樣密度不均勻的情形,該算法繼續采用一個半徑更大的球重復上述過程。該算法運算效率高,內存消耗小,且對噪聲穩健。算法具有與點數成線性關系的運算復雜度,其在運算過程中無需將點云的所有點同時導入到內存中,且生成的網格亦可增量式的保存到計算機外存中,因此適用于大數據點云的網格化。
3.7.4 Power Crust算法
Amenta 等[13]提出了一種 power crust 算法用于三維表面重建。該算法首先由點云計算物體的中心軸,并以包含在物體內部的最大球來表示物體,從而對中心軸進行逆變換獲得物體的表面。對于復雜的三維物體表面,難以準確地計算其中心軸,因此該算法采用點云的 Voronoi 圖和 Power 圖對物體表面和中軸進行分段線性估計,并用一組離散的極點球(polar ball) 近似模擬中軸。接著,將極點球劃分為物體內部空間和物體外部空間兩類,最后將這兩部分極點球分離便得到輸出曲面。該算法有很強的理論性, 在實現中心軸估計的同時, 可獲得一個密封(watertight) 的三維網格,其對有銳利邊緣的物體、非均勻采樣的點云以及噪聲干擾亦有較好的效果。此外,該算法對輸入點云無特殊要求,且避免了孔洞填充等后處理操作。該算法的缺陷在于其運行速度較慢。
點云應用
三維激光掃描已在許多重大工程和典型領域里得到了廣泛的應用。從深空到地球表面,從全球范圍制圖到小區域監測,從基礎科學研究到大眾服務,三維激光掃描都展現出了與眾不同的優勢。基于點云的模型重建與目標識別在軍事和民用領域均有非常廣泛的應用前景。
4.1 深空探測
深空探測的目的是促進人類對月球以及更遠天體的科學認識,而距離測量是其中的關鍵技術,許多國家采用激光測高儀進行星體地形表面的測量,如1971年美國阿波羅首次進行的月球形狀測量等[1]。
4.2 精確制導自動目標識別
采用激光雷達獲得的點云可有效實現高分辨率的目標成像,實現對小樹林和偽裝網遮擋下的目標檢測與識別。麻省理工學院(MIT)開展了“七巧板(JIGSAW)”項目等研究,進行了機載激光雷達對坦克和裝甲車等地面目標的檢測識別外場試驗[2-3]。該研究成果將成為美國陸軍未來戰場系統(Future Combat Systems,FCS)的一部分。瑞典國防研究局[4]、西班牙國防部[5]以及德國光子與模式識別研究所[6]等都開展了大量相關研究。
4.3 地球科學應用研究
數字地面模型是各種地學過程研究的基礎,利用三維激光掃描系統觀測地表形態及其變化,已被廣泛應用于各類地學應用,例如:全球冰川物質平衡[7-8],地質災害區域時空變化監測[9-10],海岸線提取[11-12],海底測繪及水下目標探測[13]等。
4.4 森林資源調查
及時準確了解林區的植被動態變化是林業科學研究的基礎。相比光學遙感,激光雷達能夠獲取植被冠層的三維結構;地面激光雷達用于精細地獲取單株數木的垂直結構[14],機載激光雷達用于大范圍森林的蓄積量和生物量等生態參數的反演[15-17],星載激光雷達還可以進行全球植被覆蓋及其生態參數制圖[18-19]。
4.5 城市形態分析
城市形態分析對城市規劃設計于管理具有重要意義,傳統手段難以監測城市形態的垂直結構及其演化,激光雷達可以快速獲取城市三維形態,為更精細的城市形態分析提供基礎,滿足基于城市形態的各種應用需求,如基礎設施管理、太陽能潛力估計等[20-21]。
4.6 災難救援與應急響應
采用激光雷達可獲得城市場景的真實三維模型,實現地物分類以及應急響應。麻省理工學院利用ALIRT機載激光雷達成像研究試驗平臺對太子港進行了三維成像,獲得30m分辨率的城市三維圖像,用于評估道路和橋梁狀況、分析水淹情況、選擇直升機降落場以及規劃難民安置等[22]。
4.7 無人系統自動導航
高精度地圖是實現自動化駕駛的關鍵因素。車載激光掃描系統可以高效、快速的獲取道路以及周邊高精度、高密度的三維幾何信息和紋理信息,為高精度地圖的自動化生產提供高質量的數據支撐[23]。
點云傳感器被廣泛應用于各種無人自主系統中。無論是谷歌無人車、普林斯頓大學無人車還是國防科大開發的無人車,均采用激光雷達或立體視覺獲取點云以生成車輛周圍環境的三維地圖,并結合其它傳感器實現車輛、建筑物、行人以及路牌等的檢測識別,最終完成態勢感知[24,25]。此外,德國弗萊堡大學、英國牛津大學等聯合開展了用于室外和室內場所的機器人自動導航研究,該研究將點云傳感器作為其主要傳感器之一[26]。
4.8 文物三維數字化
文化遺產數字化保護是人類共同的歷史責任。三維激光掃描可以快速繪制物質文化遺產的結構圖和精細的三維模型,大幅提高文化遺產保護的工作效率,并豐富文化遺產成果表現形式[27-28]。
采用點云傳感器對文物進行掃描進而構建三維模型有利于重要文物遺產的長期保存和修復。美國斯坦福大學與華盛頓大學合作開展了“數字化米開朗琪羅項目”,完成了對其雕刻作品的數字化三維模型重建[29]。德國NavVis公司完成了德意志博物館船舶展廳的三維全數字化建模并構建了網上三維展示,國內相關單位亦開展了對秦始皇兵馬俑等藝術作品三維數字化的探索。武漢市測繪研究院劉永鋒等[38]采用徠卡P40激光掃描儀獲取歷史建筑物內外部結構的三維點云數據,最終以CAD線劃圖的形式還原了建筑物原貌。
4.9 電力走廊安全巡檢
我國電力資源分布和經濟建設中心不一致,高壓輸電線路區域地理環境復雜,傳統的人工巡檢手段難以適應。機載三維激光掃描可以直接獲取電力線及其附屬設備的幾何形態參數[30],為電力巡檢提供了新的手段[31]。
4.10 海島礁測繪
精確的海島礁基礎地理空間信息是海洋管理、經濟開發、國防安全的重要依據,傳統測繪手段作業周期長、成本高,三維激光掃描可以直接觀測目標的三維空間信息,直接生產數字測繪產品,是島礁高精度測圖的重要手段。
4.11 隧道斷面提取與變形監測
荷蘭代爾夫特理工大學 Lindenbergh R 等[32]于 2004 年使用徠卡公司生產的 Leica HDS3000 型三維激光掃描儀對一條約 100 米長的隧道進行了點云掃描及特征點及特征斷面截取,對數據精度進行了評定,證明了三維激光掃描技術在隧道變形監測中的可行性。
荷蘭代爾夫特理工大學 Gosliga R V 等[33]在前人研究的基礎上于 2006 年引入圓的幾何模型及最小二乘算法,將三維激光掃描技術應用于圓柱形隧道橫斷面的提取中。
近十余年來,三維激光掃描技術在隧道變形監測中的應用逐漸被國內業內學者所關注和認可。同濟大學周奇才[34]等于 2010 年將激光測距技術引入到地鐵隧道斷面變形監測工作之中,激光測距技術是三維激光掃描技術的核心,故該項研究為國內的三維激光掃描技術在隧道斷面提取中的研究打下了基礎。武漢大學簡驍[35]等于2011年提出利用三次埃爾米特差值的方法對隧道點云數據進行變形曲面擬合,進而比對多期隧道曲面數據而達到變形監測的目的。武漢大學托雷[36]等于 2013 年對隧道中軸線及斷面提取進行了研究,引入 RANSAC 算法實現隧道連續斷面的截取并擬合變形曲線,實現了三維激光掃描點云數據在隧道變形監測中的應用。長安大學李雙[37]等于 2015 年提出了利用三維不變矩擬合隧道中軸線并利用二階矩擬合斷面橢圓特征的方法,實現了隧道斷面的連續提取。
此外,三維激光掃描被逐漸應用于橋梁[39]、礦山邊坡[40]的變形監測中。
三維點云的進展、挑戰與展望
5.1重要進展
近年來,國內外學者在點云處理理論以及數據質量改善、自動化融合、點云分類和目標提取、按需多層次表達等方法方面進行了深入研究,取得的主要進展如下。
5.1.1廣義點云模型理論方法
針對多源多平臺點云數據的融合難、目標提取難和三維自適應表達難的嚴重缺陷,文獻[1]提出了廣義點云的科學概念與理論研究框架體系。廣義點云是指匯集激光掃描、攝影測量、眾源采集等多源多平臺空間數據,通過清洗、配準與集成,實現從多角度、視相關到全方位、視無關,建立以點云為基礎,基準統一,且數據、結構、功能為一體的復合模型。
5.1.2三維點云數據質量改善
點云數據質量改善包括幾何改正和強度校正。一方面,由于測距系統、環境及定位定姿等因素的影響,點云的幾何位置存在誤差,且其分布存在不確定性。利用標定場、已知控制點進行點云幾何位置改正,能夠提高掃描點云的位置精度和可用性。另一方面,激光點云的反射強度一定程度上反映了地物的物理特性,對于地物的精細分類起到關鍵支撐作用,然而點云的反射強度不僅與地物表面的物理特性有關,還受到掃描距離、入射角度等因素的影響。因此,需要建立點云強度校正模型進行校正,以修正激光入射角度、地物距離激光掃描儀的距離等因素對點云反射強度的影響[2,3]。
5.1.3多源、多平臺三維點云融合
由于單一視角、單一平臺的觀測范圍有限且空間基準不一致,為了獲取目標區域全方位的空間信息,不僅需要進行站間/條帶間的點云融合,還需要進行多平臺(如機載、車載、地面站等)的點云融合,以彌補單一視角、單一平臺帶來的數據缺失,實現大范圍場景完整、精細的數字現實描述[4-6]。此外,由于激光點云及其強度信息對目標的刻畫能力有限,需要將激光點云和影像數據進行融合,使得點云不僅有高精度的三維坐標信息,也具有了更加豐富的光譜信息[7,8]。不同數據(如不同站點/條帶的激光點云、不同平臺激光點云、激光點云與影像)之間的融合,需要同名特征進行關聯。針對傳統人工配準法效率低、成本高的缺陷,國內外學者研究基于幾何或紋理特征相關性的統計分析方法[9-10],但是由于不同平臺、不同傳感器數據之間的成像機理、維數、尺度、精度、視角等各有不同,其普適性和穩健性還存在問題,還需要突破以下瓶頸:魯棒、區分性強的同名特征提取,全局優化配準模型的建立及抗差求解。
5.1.4三維點云的精細分類與目標提取
三維點云的精細分類是從雜亂無序的點云中識別與提取人工與自然地物要素的過程,是數字地面模型生成、復雜場景三維重建等后續應用的基礎。然而,不同平臺激光點云分類關注的主題有所不同。機載激光點云分類主要關注大范圍地面、建筑物頂面、植被、道路等目標[11-16],車載激光點云分類關注道路及兩側道路設施、植被、建筑物立面等目標[17-20],而地面站激光點云分類則側重特定目標區域的精細化解譯[21]。其中,點云場景存在目標多樣、形態結構復雜、目標遮擋和重疊以及空間密度差別迥異等現象,是三維點云自動精細分類的共同難題。
據此,國內外許多學者進行了深入研究并取得了一定的進展,在特征計算基礎上,利用逐點分類方法[22-23]或分割聚類分類方法[17-19]對點云標識,并對目標進行提取。但是由于特征描述能力不足,分類和目標提取質量無法滿足應用需求,極大地限制了三維點云的使用價值。目前,模擬人腦的深度學習方法突破了傳統分類方法中過度依賴人工定義特征的困難,已在二維場景分類解譯方面表現出極大潛力[24],但是在三維點云場景的精細分類方面,還面臨許多難題:海量三維數據集樣本庫的建立,適用于三維結構特征學習的神經網絡模型的構建及其在大場景三維數據解譯中的應用。綜上,顧及目標及其結構的語義理解,三維目標多尺度全局與局部特征的學習,先驗知識或第三方輔助數據引導下的多目標分類與提取方法,是未來的重要研究方向。
5.1.5三維場景的按需多層次表達
在大范圍點云場景分類和目標提取后,目標點云依然離散無序且高度冗余,不能顯式地表達目標結構以及結構之間的空間拓撲關系,難以有效滿足三維場景的應用需求。因此,需要通過場景三維表達,將離散無序的點云轉換成具有拓撲關系的幾何基元組合模型,常用的有數據驅動和模型驅動兩類方法[25-26],其中存在的主要問題和挑戰包括:三維模型的自動修復,以克服局部數據缺失對模型不完整的影響[27];形狀、結構復雜地物目標的自動化穩健重構;從可視化為主的三維重建發展到可計算分析為核心的三維重建,以提高結果的可用性和好用性。此外,不同的應用主題對場景內不同類型目標的細節層次要求不同[28],場景三維表達需要加強各類三維目標自適應的多尺度三維重建方法[29-30],建立語義與結構正確映射的場景—目標—要素多級表達模型。
5.2面臨挑戰
近年來,星、空、地掃描以及便攜式泛在傳感器(如:RGB-D 深度相機)廣泛運用,不但提高了點云獲取的時效性、顆粒度和覆蓋面,而且帶來了點云的多時相、流形(streaming)和多樣屬性的新特性,從而產生了多維點云數據。多維點云本質上是對物理世界中地理對象/現象的三維幾何、物理乃至生化特性的多維密集采樣,其不但記錄了地物的三維空間結構特征,同時也記錄了地物目標的物理特性(如波形、反射強度等)。深入挖掘多維點云的內在特征對提升多維點云處理的智能化程度,揭示復雜動態三維場景的變化規律至關重要。盡管點云處理方面已經取得了較好的研究成果,但是多維點云的智能化處理方面仍然面臨如下的巨大挑戰:
5.2.1多維點云幾何與屬性協同的尺度轉換
探索不同平臺獲取點云的誤差分布規律,建立比例尺依賴的特征點質量評估模型;研究融合點云物理特性的特征點簇聚合與分層方法;建立基于特征分層的多維點云多尺度整合方法,實現多維點云的時空基準自動統一。
5.2.2多維點云變化發現與分類
建立統一時空參考框架下多維點云的變化發現與提取方法,研究基于時間窗口的多維點云與地物三維模型的關聯方法,提取地物空間要素的幾何和屬性變化,研究面向地物空間結構變化的可視化分析方法,為揭示空間要素的變化規律提供科學工具。
5.2.3復雜三維動態場景的精準理解
基于機器學習、人工智能等先進理論方法探索多維點云結構化建模與分析的理論與方法,研究建立復雜三維動態場景中多態目標的準確定位、分類以及語義化模型的建立,建立面向多維點云的三維動態場景中各類要素的特征描述、分類與建模方法,架設多維點云與地理計 算模型的橋梁。
上述關鍵挑戰問題的突破將形成完備的廣義點云全三維(覆蓋全、要素全、關系全)建模的理論與方法體系,從而實現點云處理由“靜態、可視、量算”到“動態、模擬、分析”的跨越。
5.3 發展趨勢與展望
近年來,傳感器、通信和定位定姿技術的發展,人工智能、深度學習、虛擬/增強現實等領域先進技術的重要進展有力推動了數字現實(digital reality)時代的來臨。激光掃描與點云智能化處理將順應數字現實時代的需求朝以下幾個方面發展。
⑴三維激光掃描裝備將由現在的單波形、多波形走向單光子乃至量子雷達,在數據的采集方面由現在已幾何數據為主走向幾何、物理,乃至生化特性的集成化采集。
⑵三維激光掃描的搭載平臺也將以單一平臺為主轉變為以多源化、眾包式為主的空地柔性平臺,從而對目標進行全方位數據獲取,當前國家重點研發計劃重點專項項目:國產空地全息三維遙感系統及產業化已支持相關研究。
⑶點云的特征描述、語義理解、關系表達、目標語義模型、多維可視化等關鍵問題將在人工智能、深度學習等先進技術的驅動下朝著自動化、智能化的方向快速發展,點云將成為測繪地理信息中繼傳統矢量模型、柵格模型之后的一類新型模型,將有力提升地物目標認知與提取自動化程度和知識化服務的能力。
⑷虛擬/增強現實、互/物聯網+的發展將促使三維激光掃描產品由專業化應用擴展到大眾化、消費級應用,滿足網絡化多維動態地理信息服務的需求。
-
算法
+關注
關注
23文章
4622瀏覽量
93060 -
激光雷達
+關注
關注
968文章
3991瀏覽量
190080 -
點云
+關注
關注
0文章
58瀏覽量
3804
原文標題:點云綜述:點云硬件、點云軟件、點云處理算法、點云應用以及點云的挑戰與展望
文章出處:【微信號:vision263com,微信公眾號:新機器視覺】歡迎添加關注!文章轉載請注明出處。
發布評論請先 登錄
相關推薦
基于深度學習的三維點云分類方法
什么是三維點云分割
輸電線路激光雷達點云監測裝置的功能特點和技術參數介紹
激光雷達點云數據包含哪些信息
友思特方案 基于三維點云實現PCB裝配螺絲視覺檢測

激發云服務效能,華為云 Flexus X 實例助力破除中小企上云痛點

重塑云服務,華為云 Flexus X 實例破解云服務傳統難題

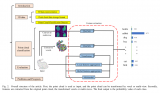
友思特案例 | 自研創新!三維工件尺寸測量及點云處理解決方案
華為云這款產品性能超越獨享實例,企業數字化升級首選!
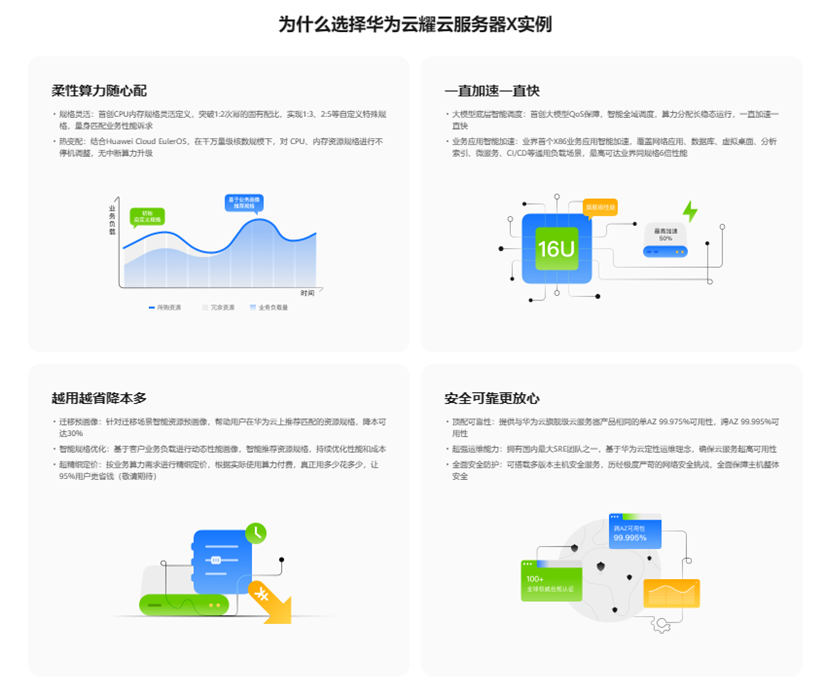
泰來三維|三維掃描服務_三維激光掃描儀測量山體滑坡點云建模
電梯物聯網技術如何解決電梯管理的痛點?
基于深度學習的方法在處理3D點云進行缺陷分類應用
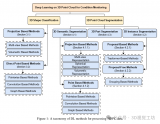




 點云綜述以及點云的挑戰與展望
點云綜述以及點云的挑戰與展望










評論