本篇文章講解了計算機的原碼， 反碼和補碼。 并且進行了深入探求了為何要使用反碼和補碼， 以及更進一步的論證了為何可以用反碼， 補碼的加法計算原碼的減法。 論證部分如有不對的地方請各位牛人幫忙指正！ 希望本文對大家學習計算機基礎有所幫助！

一、機器數和真值

在學習原碼， 反碼和補碼之前， 需要先了解機器數和真值的概念。

1、機器數

一個數在計算機中的二進制表示形式， 叫做這個數的機器數。機器數是帶符號的，在計算機用一個數的最高位存放符號， 正數為0， 負數為1.

比如，十進制中的數 +3 ，計算機字長為8位，轉換成二進制就是00000011。如果是 -3 ，就是 10000011 。

那么，這里的 00000011 和 10000011 就是機器數。

2、真值

因為第一位是符號位，所以機器數的形式值就不等于真正的數值。例如上面的有符號數 10000011，其最高位1代表負，其真正數值是 -3 而不是形式值131（10000011轉換成十進制等于131）。所以，為區別起見，將帶符號位的機器數對應的真正數值稱為機器數的真值。

例：0000 0001的真值 = +000 0001 = +1，1000 0001的真值 = –000 0001 = –1

二、原碼， 反碼， 補碼的基礎概念和計算方法。

在探求為何機器要使用補碼之前， 讓我們先了解原碼， 反碼和補碼的概念。對于一個數， 計算機要使用一定的編碼方式進行存儲。 原碼， 反碼， 補碼是機器存儲一個具體數字的編碼方式。

1、原碼

原碼就是符號位加上真值的絕對值， 即用第一位表示符號， 其余位表示值。 比如如果是8位二進制：

［+1］ 原 = 0000 0001

［-1］ 原 = 1000 0001

第一位是符號位。 因為第一位是符號位， 所以8位二進制數的取值范圍就是：

［1111 1111 ， 0111 1111］

即

［-127 ， 127］

原碼是人腦最容易理解和計算的表示方式。

2、反碼

反碼的表示方法是：

正數的反碼是其本身

負數的反碼是在其原碼的基礎上， 符號位不變，其余各個位取反。

［+1］ = ［00000001］ 原 = ［00000001］ 反

［-1］ = ［10000001］ 原 = ［11111110］ 反

可見如果一個反碼表示的是負數， 人腦無法直觀的看出來它的數值。 通常要將其轉換成原碼再計算。

3、補碼

補碼的表示方法是：

正數的補碼就是其本身

負數的補碼是在其原碼的基礎上， 符號位不變， 其余各位取反， 最后+1. （即在反碼的基礎上+1）

［+1］ = ［00000001］ 原 = ［00000001］ 反 = ［00000001］ 補

［-1］ = ［10000001］ 原 = ［11111110］ 反 = ［11111111］ 補

對于負數， 補碼表示方式也是人腦無法直觀看出其數值的。 通常也需要轉換成原碼在計算其數值。

三、為何要使用原碼， 反碼和補碼

在開始深入學習前， 我的學習建議是先“死記硬背”上面的原碼， 反碼和補碼的表示方式以及計算方法。

現在我們知道了計算機可以有三種編碼方式表示一個數。 對于正數因為三種編碼方式的結果都相同：

［+1］ = ［00000001］ 原 = ［00000001］ 反 = ［00000001］ 補

所以不需要過多解釋。 但是對于負數：

［-1］ = ［10000001］ 原 = ［11111110］ 反 = ［11111111］ 補

可見原碼， 反碼和補碼是完全不同的。 既然原碼才是被人腦直接識別并用于計算表示方式， 為何還會有反碼和補碼呢？

首先， 因為人腦可以知道第一位是符號位， 在計算的時候我們會根據符號位， 選擇對真值區域的加減。 （真值的概念在本文最開頭）。 但是對于計算機， 加減乘數已經是最基礎的運算， 要設計的盡量簡單。 計算機辨別“符號位”顯然會讓計算機的基礎電路設計變得十分復雜！ 于是人們想出了將符號位也參與運算的方法。 我們知道， 根據運算法則減去一個正數等于加上一個負數， 即： 1-1 = 1 + （-1） = 0 ， 所以機器可以只有加法而沒有減法， 這樣計算機運算的設計就更簡單了。

于是人們開始探索 將符號位參與運算， 并且只保留加法的方法。 首先來看原碼：

計算十進制的表達式： 1-1=0

1 - 1 = 1 + （-1） = ［00000001］ 原 + ［10000001］ 原 = ［10000010］ 原 = -2

如果用原碼表示， 讓符號位也參與計算， 顯然對于減法來說， 結果是不正確的。這也就是為何計算機內部不使用原碼表示一個數。

為了解決原碼做減法的問題， 出現了反碼：

計算十進制的表達式： 1-1=0

1 - 1 = 1 + （-1） = ［0000 0001］ 原 + ［1000 0001］ 原= ［0000 0001］ 反 + ［1111 1110］ 反 = ［1111 1111］ 反 = ［1000 0000］ 原 = -0

發現用反碼計算減法， 結果的真值部分是正確的。 而唯一的問題其實就出現在“0”這個特殊的數值上。 雖然人們理解上+0和-0是一樣的， 但是0帶符號是沒有任何意義的。 而且會有［0000 0000］原和［1000 0000］原兩個編碼表示0.

于是補碼的出現， 解決了0的符號以及兩個編碼的問題：

1-1 = 1 + （-1） = ［0000 0001］ 原 + ［1000 0001］ 原 = ［0000 0001］ 補 + ［1111 1111］ 補 = ［0000 0000］ 補=［0000 0000］ 原

這樣0用［0000 0000］表示， 而以前出現問題的-0則不存在了。而且可以用［1000 0000］表示-128：

（-1） + （-127） = ［1000 0001］ 原 + ［1111 1111］ 原 = ［1111 1111］ 補 + ［1000 0001］ 補 = ［1000 0000］ 補

-1-127的結果應該是-128， 在用補碼運算的結果中， ［1000 0000］補 就是-128. 但是注意因為實際上是使用以前的-0的補碼來表示-128， 所以-128并沒有原碼和反碼表示。（對-128的補碼表示［1000 0000］補算出來的原碼是［0000 0000］原， 這是不正確的）

使用補碼， 不僅僅修復了0的符號以及存在兩個編碼的問題， 而且還能夠多表示一個最低數。 這就是為什么8位二進制， 使用原碼或反碼表示的范圍為［-127， +127］， 而使用補碼表示的范圍為［-128， 127］。

因為機器使用補碼， 所以對于編程中常用到的32位int類型， 可以表示范圍是： ［-231， 231-1］ 因為第一位表示的是符號位。而使用補碼表示時又可以多保存一個最小值。

四、原碼， 反碼， 補碼 再深入

計算機巧妙地把符號位參與運算， 并且將減法變成了加法， 背后蘊含了怎樣的數學原理呢？

將鐘表想象成是一個1位的12進制數。 如果當前時間是6點， 我希望將時間設置成4點， 需要怎么做呢？我們可以：

1. 往回撥2個小時： 6 - 2 = 4

2. 往前撥10個小時： （6 + 10） mod 12 = 4

3. 往前撥10+12=22個小時： （6+22） mod 12 =4

2，3方法中的mod是指取模操作， 16 mod 12 =4 即用16除以12后的余數是4.

所以鐘表往回撥（減法）的結果可以用往前撥（加法）替代！

現在的焦點就落在了如何用一個正數， 來替代一個負數。 上面的例子我們能感覺出來一些端倪， 發現一些規律。 但是數學是嚴謹的。 不能靠感覺。

首先介紹一個數學中相關的概念： 同余

同余的概念

兩個整數a，b，若它們除以整數m所得的余數相等，則稱a，b對于模m同余

記作 a ≡ b （mod m）

讀作 a 與 b 關于模 m 同余。

舉例說明：

4 mod 12 = 4

16 mod 12 = 4

28 mod 12 = 4

所以4， 16， 28關于模 12 同余。

負數取模

正數進行mod運算是很簡單的。 但是負數呢？

下面是關于mod運算的數學定義：

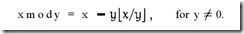
上面是截圖， “取下界”符號找不到如何輸入（word中粘貼過來后亂碼）。 下面是使用“L”和“J”替換上圖的“取下界”符號：

x mod y = x - y L x / y J

上面公式的意思是：

x mod y等于 x 減去 y 乘上 x與y的商的下界。

以 -3 mod 2 舉例：

-3 mod 2

= -3 - 2xL -3/2 J

= -3 - 2xL-1.5J

= -3 - 2x（-2）

= -3 + 4 = 1

所以：

（-2） mod 12 = 12-2=10

（-4） mod 12 = 12-4 = 8

（-5） mod 12 = 12 - 5 = 7

開始證明

再回到時鐘的問題上：

回撥2小時 = 前撥10小時

回撥4小時 = 前撥8小時

回撥5小時= 前撥7小時

注意， 這里發現的規律！

結合上面學到的同余的概念。實際上：

（-2） mod 12 = 10

10 mod 12 = 10

-2與10是同余的。

（-4） mod 12 = 8

8 mod 12 = 8

-4與8是同余的。

距離成功越來越近了。 要實現用正數替代負數， 只需要運用同余數的兩個定理：

反身性：

a ≡ a （mod m）

這個定理是很顯而易見的。

線性運算定理：

如果a ≡ b （mod m），c ≡ d （mod m） 那么：

（1）a ± c ≡ b ± d （mod m）

（2）a * c ≡ b * d （mod m）

如果想看這個定理的證明， 請看：http://baike.baidu.com/view/79282.htm

所以：

7 ≡ 7 （mod 12）

（-2） ≡ 10 （mod 12）

7 -2 ≡ 7 + 10 （mod 12）

現在我們為一個負數， 找到了它的正數同余數。 但是并不是7-2 = 7+10， 而是 7 -2 ≡ 7 + 10 （mod 12） ， 即計算結果的余數相等。

接下來回到二進制的問題上， 看一下： 2-1=1的問題。

2-1=2+（-1） = ［0000 0010］ 原 + ［1000 0001］ 原= ［0000 0010］ 反 + ［1111 1110］ 反

先到這一步， -1的反碼表示是1111 1110. 如果這里將［1111 1110］認為是原碼， 則［1111 1110］原 = -126， 這里將符號位除去， 即認為是126.

發現有如下規律：

（-1） mod 127 = 126

126 mod 127 = 126

即：

（-1） ≡ 126 （mod 127）

2-1 ≡ 2+126 （mod 127）

2-1 與 2+126的余數結果是相同的！ 而這個余數， 正式我們的期望的計算結果： 2-1=1

所以說一個數的反碼， 實際上是這個數對于一個膜的同余數。 而這個膜并不是我們的二進制， 而是所能表示的最大值！ 這就和鐘表一樣， 轉了一圈后總能找到在可表示范圍內的一個正確的數值！

而2+126很顯然相當于鐘表轉過了一輪， 而因為符號位是參與計算的， 正好和溢出的最高位形成正確的運算結果。

既然反碼可以將減法變成加法， 那么現在計算機使用的補碼呢？ 為什么在反碼的基礎上加1， 還能得到正確的結果？

2-1=2+（-1） = ［0000 0010］ 原 + ［1000 0001］ 原 = ［0000 0010］ 補 + ［1111 1111］ 補

如果把［1111 1111］當成原碼， 去除符號位， 則：

［0111 1111］ 原 = 127

其實， 在反碼的基礎上+1， 只是相當于增加了膜的值：

（-1） mod 128 = 127

127 mod 128 = 127

2-1 ≡ 2+127 （mod 128）

此時， 表盤相當于每128個刻度轉一輪。 所以用補碼表示的運算結果最小值和最大值應該是［-128， 128］。

但是由于0的特殊情況， 沒有辦法表示128， 所以補碼的取值范圍是［-128， 127］