SVM 是機(jī)器學(xué)習(xí)領(lǐng)域的經(jīng)典算法之一。如果將 SVM推廣到神經(jīng)網(wǎng)絡(luò)，會(huì)發(fā)生什么呢？

支持向量機(jī)（Support Vector Machine，SVM）是大多數(shù) AI 從業(yè)者比較熟悉的概念。它是一種在分類(lèi)與回歸分析中分析數(shù)據(jù)的監(jiān)督式學(xué)習(xí)模型與相關(guān)的學(xué)習(xí)算法。給定一組訓(xùn)練實(shí)例，每個(gè)訓(xùn)練實(shí)例被標(biāo)記為屬于兩個(gè)類(lèi)別中的一個(gè)或另一個(gè)，SVM 訓(xùn)練算法創(chuàng)建一個(gè)將新的實(shí)例分配給兩個(gè)類(lèi)別之一的模型，使其成為非概率二元線(xiàn)性分類(lèi)器。SVM 模型將實(shí)例表示為空間中的點(diǎn)，這樣映射就使得單獨(dú)類(lèi)別的實(shí)例被盡可能寬的明顯的間隔分開(kāi)。然后，將新的實(shí)例映射到同一空間，并基于它們落在間隔的哪一側(cè)來(lái)預(yù)測(cè)所屬類(lèi)別。 除了進(jìn)行線(xiàn)性分類(lèi)之外，SVM 還可以使用所謂的核技巧有效地進(jìn)行非線(xiàn)性分類(lèi)，將其輸入隱式映射到高維特征空間中。 本文將介紹一篇來(lái)自蒙特利爾大學(xué)的論文《SVM、Wasserstein 距離、梯度懲罰 GAN 之間的聯(lián)系》。在這篇論文中，研究者闡述了如何從同一框架中得到 SVM 和梯度懲罰 GAN。 據(jù)論文一作介紹，這項(xiàng)研究的靈感來(lái)自她的博士資格考試。在準(zhǔn)備過(guò)程中，她學(xué)習(xí)了 SVM，并思考了這個(gè)問(wèn)題：「如果將 SVM 推廣到神經(jīng)網(wǎng)絡(luò)會(huì)發(fā)生什么？」順著這個(gè)思路，研究者發(fā)現(xiàn)了 SVM、GAN、Wasserstein 距離之間的關(guān)系。

該研究將最大間隔分類(lèi)器（MMC）的概念擴(kuò)展到任意范數(shù)和非線(xiàn)性函數(shù)。支持向量機(jī)是 MMC 的一個(gè)特例。研究者發(fā)現(xiàn)，MMC 可以形式化為積分概率度量（Integral Probability Metrics，IPM）或具備某種形式梯度范數(shù)懲罰的分類(lèi)器。這表明它與梯度懲罰 GAN 有直接關(guān)聯(lián)。 該研究表明，Wasserstein GAN、標(biāo)準(zhǔn) GAN、最小二乘 GAN 和具備梯度懲罰的 Hinge GAN 中的判別器都是 MMC，并解釋了 GAN 中最大化間隔的作用。研究者假設(shè) L^∞ 范數(shù)懲罰和 Hinge 損失生成的 GAN 優(yōu)于 L^2 范數(shù)懲罰生成的 GAN，并通過(guò)實(shí)驗(yàn)進(jìn)行了驗(yàn)證。此外，該研究還導(dǎo)出了 Relativistic paired (Rp) 和 average (Ra) GAN 的間隔。 這篇論文共包含幾部分：在第二章中，研究者回顧了 SVM 和 GAN；第三章，研究者概述了最大間隔分類(lèi)器（MMC）的概念；第四章，研究者用梯度懲罰解釋了 MMC 和 GAN 之間的聯(lián)系。其中 4.1 提到了強(qiáng)制 1-Lipschitz 等價(jià)于假設(shè)一個(gè)有界梯度，這意味著 Wasserstein 距離可以用 MMC 公式來(lái)近似估算；4.2 描述了在 GAN 中使用 MMC 的好處；4.3 假定 L1 范數(shù)間隔能夠?qū)е赂唪敯粜缘姆诸?lèi)器；4.4 推導(dǎo)了 Relativistic paired GAN 和 Relativistic average GAN 的間隔。最后，第五章提供了實(shí)驗(yàn)結(jié)果以支持文章假設(shè)。 SVM 是 MMC 的一個(gè)特例。MMC 是使間隔最大化的分類(lèi)器 f（間隔指的是決策邊界與數(shù)據(jù)點(diǎn)之間的距離）。決策邊界是指我們無(wú)法分辨出樣本類(lèi)別的區(qū)域（所有 x 使得 f(x)=0）。 Soft-SVM 是一種特殊情況，它可以使最小 L2 范數(shù)間隔最大化。下圖展示了實(shí)際使用中的 Soft-SVM：

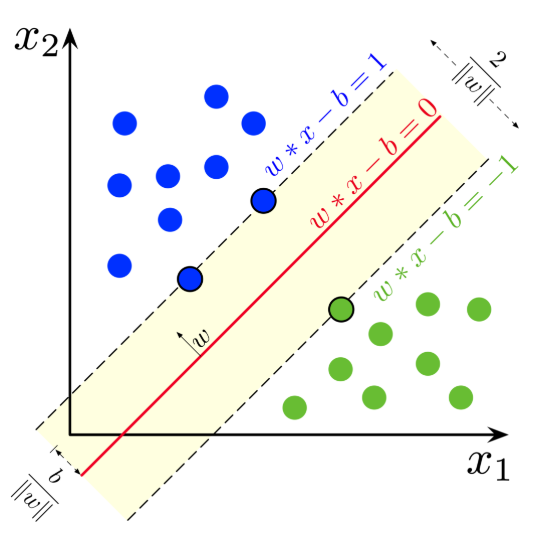
在解釋這一結(jié)果之前，我們需要了解一個(gè)關(guān)鍵要素。關(guān)于「間隔」有多種定義： （1）樣本與邊界之間的最小距離； （2）距邊界最近的點(diǎn)與邊界之間的最小距離。 定義（2）更為常用。但是如果使用此定義，那么 SVM 文獻(xiàn)中所謂的「函數(shù)間隔（functional margin）」和「幾何間隔（geometric margin）」就都不能被視為間隔。這可能會(huì)讓人十分困惑。 理解這種差異更好的一種方式是：

將（1）視為「樣本的間隔」；

將（2）視為「數(shù)據(jù)集的間隔」。

但是，為了消除這兩種情況的歧義，本文將前者稱(chēng)為「間隔（margin）」，將后者稱(chēng)為「最小間隔（minimum margin）」。 Hard-SVM（原始形式）解決了最大化最小間隔的問(wèn)題。Soft-SVM 解決了另一個(gè)更簡(jiǎn)單的問(wèn)題——最大化期望 soft-margin（最小化期望 Hinge 損失）。這個(gè)問(wèn)題很容易解決，hinge 損失確保遠(yuǎn)離邊界的樣本不會(huì)對(duì)假重復(fù) Hard-SVM 效果的嘗試產(chǎn)生任何影響。 從這個(gè)角度看，最大化期望間隔（而不是最大化最小間隔）仍會(huì)導(dǎo)致最大間隔分類(lèi)器，但是分類(lèi)器可能會(huì)受到遠(yuǎn)離邊界的點(diǎn)的影響（如果不使用 Hinge 損失的話(huà)）。因此，最大化期望間隔意味著最大化任何樣本（即數(shù)據(jù)點(diǎn)）與決策邊界之間的平均距離。這些方法就是最大間隔分類(lèi)器（MMC）的示例。 為了盡可能地通用化，該研究設(shè)計(jì)了一個(gè)框架來(lái)導(dǎo)出 MMC 的損失函數(shù)。研究者觀(guān)察到，該框架可以導(dǎo)出帶有梯度懲罰的基于間隔的目標(biāo)函數(shù)（目標(biāo)函數(shù) F 的形式為 F(yf(x))）。這就意味著標(biāo)準(zhǔn) GAN、最小二乘 GAN、WGAN 或 HingeGAN-GP 都是 MMC。所有這些方法（和 WGAN-GP 一樣使用 L2 梯度規(guī)范懲罰時(shí)）都能最大化期望 L2 范數(shù)間隔。 研究者還展示了，使用 Lipschitz-1 判別器的大多數(shù) GAN（譜歸一化 HingeGAN、WGAN、WGAN-GP 等）都可被表示為 MMC，因?yàn)榧俣?1-Lipschitz 等效于假定有界梯度（因此可作為一種梯度懲罰形式）。 重要的是，這意味著我們可以將最成功的 GAN（BigGAN、StyleGAN）看作 MMC。假定 Lipschitz-1 判別器一直被看作實(shí)現(xiàn)優(yōu)秀 GAN 的關(guān)鍵因素，但它可能需要一個(gè)能夠最大化間隔的判別器和相對(duì)判別器（Relativistic Discriminator）。該研究基于 MMC 判別器給偽生成樣本帶來(lái)更多梯度信號(hào)的事實(shí)，闡述了其優(yōu)點(diǎn)。 在這一點(diǎn)上，讀者可能有疑問(wèn)：「是不是某些間距比其它間距更好？是的話(huà)，我們能做出更好的 GAN 嗎？」 這兩個(gè)問(wèn)題的答案都是肯定的。最小化 L1 范數(shù)的損失函數(shù)比最小化 L2 范數(shù)的損失函數(shù)對(duì)異常值更具魯棒性。基于這一事實(shí)，研究者提出質(zhì)疑：L1 范數(shù)間隔會(huì)帶來(lái)魯棒性更強(qiáng)的分類(lèi)器，生成的 GAN 也可能比 L2 范數(shù)間隔更佳。 重要的是，L1 范數(shù)間隔會(huì)造成 L∞ 梯度范數(shù)懲罰，L2 范數(shù)間隔會(huì)造成 L2 梯度范數(shù)懲罰。該研究進(jìn)行了一些實(shí)驗(yàn)，表明 L∞ 梯度范數(shù)懲罰（因使用 L1 間隔產(chǎn)生）得到的 GAN 性能更優(yōu)。 此外，實(shí)驗(yàn)表明， HingeGAN-GP 通常優(yōu)于 WGAN-GP（這是說(shuō)得通的，因?yàn)?hinge 損失對(duì)遠(yuǎn)離邊界的異常值具有魯棒性），并且僅懲罰大于 1 的梯度范數(shù)效果更好（而不是像 WGAN-GP 一樣，使所有的梯度范數(shù)逼近 1）。因此，盡管這是一項(xiàng)理論研究，但研究者發(fā)現(xiàn)了一些對(duì)改進(jìn) GAN 非常有用的想法。 使用該框架，研究者能夠?yàn)?Relativistic paired (Rp) GAN 和 Relativistic average (Ra) GAN 定義決策邊界和間隔。人們常常想知道為什么 RpGAN 的性能不如 RaGAN，在這篇文章中，研究者對(duì)此進(jìn)行了闡述。 使用 L1 范數(shù)間隔的想法只是冰山一角，該框架還能通過(guò)更具魯棒性的間隔，設(shè)計(jì)出更優(yōu)秀的 GAN（從而提供更好的梯度懲罰或「光譜」歸一化技術(shù)）。最后，對(duì)于為什么梯度懲罰或 1-Lipschitz 對(duì)不估計(jì) Wasserstein 距離的 GAN 有效，該研究也提供了明確的理論依據(jù)，更多細(xì)節(jié)可參考原論文。