引言
卡爾曼濾波(KF)是一個不斷預測、修正的遞推過程,已經越來越多地應用于動態數據處理中。然而在KF模型中,要求觀測方程是線性形式、狀態噪聲和測量噪聲是白噪聲。為了解決這種矛盾,將KF理論應用到非線性領域中,擴展卡爾曼濾波(EKF)應用而生,它圍繞狀態估計值對非線性系統進行一階Taylor展開使其線性化,但它存在如下不足:一是當非線性函數Taylor展開式的高階項無法忽略時,會產生較大的線性化誤差;二是EKF假定噪聲均為正態白噪聲,但是一個正態自噪聲經過非線性變換后通常不再呈現正態性;三是只有在雅可比矩陣存在時才能線性化,而很多應用中雅可比矩陣很難求。針對這種情況,Julier和Uhlmann等人提出了一種基于非線性變換——Un-scented變換(UT)的卡爾曼濾波算法(UKF)。它通過確定性采樣得到的一組sigma點,可以獲得更多的觀測假設,對系統狀態的均值和協方差的估計更為準確,同時由于該算法采用了非線性的狀態方程和觀測方程,從而避免了線性化誤差。目前,EKF和UKF算法被廣泛應用于GPS非線性動態濾波研究中,并取得良好的定位效果。
本文給出了一種加權最小二乘一卡爾曼濾波(WLS-KF)算法,它利用一組離散采樣點,通過WLS方法產生近似線性化預測模型,然后用KF算法對此模型進行校正。以該算法為思路,將其應用在GPS非線性動態濾波定位解算中,仿真結果表明該算法精度介于EKF和UKF之間,從而實現了對目標較高精度的定位和跟蹤。
1 算法描述
1.1 WLS算法
LS算法是現代測量技術中數據處理的基本工具,這種方法的特點是算法簡單,在估計解算時,不需要知道與被估計量以及觀測量有關的任何統計信息。
設X為待估參數矢量,觀測矢量為L。觀測方程為:

式中:A是系數矩陣;f(X0)表示用先驗參數計算的理論觀測向量;b表示擬合后的殘差;△X是對先驗參數的小修正向量。
LS算法的指標是使各次觀測量與由參數估計得到的觀測量之差的平方和最小,即:

計算完測量更新方程后,整個過程再次重復,上一次計算得到的后驗估計被作為下一次計算的先驗估計。
1.3 WLS-KF算法
1.3.1 基本思想
算法基本思想是通過WLS方法計算隨機變量經過非線性變換后的分布參數,它利用離散個加權點來確定近似直線。
設待確定的近似線性化模型為:

2 實驗結果與分析
基于運動載體為質點的假設建立目標運動模型,考慮一個二維平面曲線運動系統,狀態定義為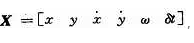 ,分別表示二維方向上的位置變量、速度變量、載體相對于起始位置的轉彎角度及接收機鐘差。?
,分別表示二維方向上的位置變量、速度變量、載體相對于起始位置的轉彎角度及接收機鐘差。?
系統狀態方程為:
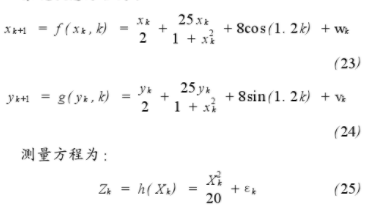
式中:wk,vk和εk為相互獨立的高斯白噪聲序列,wk~N(0,10),vk~N(0,10),εk~N(0,1)。此系統是具有可加噪聲的離散非線性時變系統,觀測時間為100 s,觀測周期為1 s。WLS-KF和EKF,UKF算法的二維預測結果分別如圖1,圖2所示,預測結果誤差分析見表1。
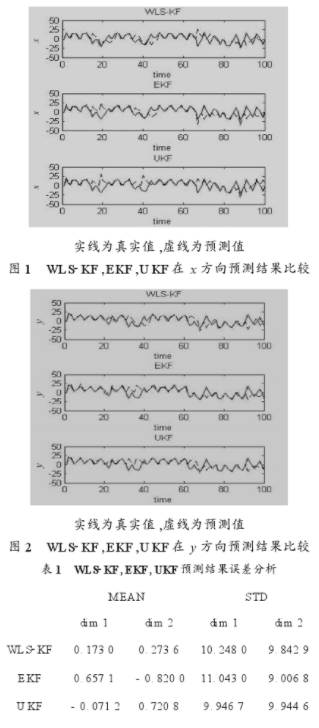
為便于比較,算法中使用的隨機數據均來自于提前保存好的隨機序列。結果表明,WLS-KF算法的計算量適中,精度介于EKF和UKF之間,且效率同KF接近。
3 結語
本文引入了一種基于加權最小二乘的線性化方法,將其與KF算法相結合,給出了可以應用于GPS非線性動態濾波系統的WLS-KF算法。該算法不需要求偏導數,算法精度介于EKF和UKF之間,可以實現對目標較高精度的定位和跟蹤,有一定的應用價值。
責任編輯:gt
-
噪聲
+關注
關注
13文章
1122瀏覽量
47442 -
濾波
+關注
關注
10文章
667瀏覽量
56686 -
函數
+關注
關注
3文章
4338瀏覽量
62751
發布評論請先 登錄
相關推薦
【TL6748 DSP申請】基于DSP的目標跟蹤算法研究及優化實現
【NUCLEO-F412ZG申請】高精度低功耗室內定位系統
【芯靈思A83T試用申請】嵌入式視覺--遠距離物體跟蹤與定位
基于QT+OpenCv的目標跟蹤算法實現
低成本高精度定位方案是未來市場趨勢,基于uwb高精度定位的案例分析
OPPO推出自研的TK 高精度定位算法 實現精度小于 1 米
OPPO推出自研RTK高精度定位算法,實現精度小于1米
基于非線性濾波和多維標度的目標跟蹤算法




 基于WLS-KF算法實現對目標較高精度的定位和跟蹤研究
基于WLS-KF算法實現對目標較高精度的定位和跟蹤研究












評論