引 言
無線傳感器網絡是面向事件的監測網絡,對于大多數應用,不知道傳感器位置而感知的數據是沒有意義的。實時地確定事件發生的位置或獲取消息的節點位置是傳感器網絡最基本的功能之一,也是提供監測事件位置信息的前提,所以定位技術對傳感器網絡應用的有效性起著關鍵的作用。
在無線傳感器網絡中,按節點位置估測機制,根據定位過程中是否測量節點間的實際距離或角度,可分為基于距離(Range—based)的定位算法和距離無關(Range—free)的定位算法。前者需要測量節點間的實際距離;后者是利用節點間的估計距離來計算末知節點的位置。在基于距離的定位算法中,測量節點間距離或方位時采用的方法有TOA(Time of Arrival),TDOA(Time Difference of Arrival),RSSI(ReceivedSignal Strength Indication)和AOA(Angle of Arri—val)。距離無關的算法主要有質心算法、DV—hop算法等。相比之下,基于距離的定位算法測量精度較高,距離無關的定位算法對硬件要求較低。
比較各種基于距離的測距算法,TOA需要精確的時鐘同步,TDOA需要節點配備超聲波收發裝置,AOA需要有天線陣列或麥克風陣列,這三種算法對硬件要求較高。RSSI技術主要是用RF信號,而節點本身就具有無線通信能力,故其是一種低功耗、廉價的測距技術。
接收信號強度指示RSSI的定位方法,是在已知發射節點的發射信號強度,根據接收節點收到的信號強度,計算出信號的傳播損耗,再利用理論和經驗模型將傳輸損耗轉化為距離,最后計算節點的位置。因為理論和經驗模型的估測性質,故而RSSI具有較大定位誤差。
基于RSSI技術,提出一種將RSSI測量方法與三角形質心算法相結合的新型定位算法,該算法用三角形質心算法減小RSSI的測量誤差。仿真表明,該算法基于RSSI的三邊測量法定位算法相比,極大提高了定位精度。
1、 國內外相關研究
當無線信號在大氣環境中傳播時,由于多種因素影響,信號強度會隨著其傳播距離的增加而衰減。這表明,信號強度變化與傳播距離間存在著某種函數關系,且通常情況下傳感節點均可很容易配置測定接收信號強度的模塊。所以,近年來研究人員開始將RSSI技術用于傳感器節點定位中。
目前,對RSSI的研究主要有兩個方面。一是,提高改良傳輸損耗模型,建立更符合實際環境的數學模型;二是,結合各種測量算法,減小傳輸損耗模型帶來的誤差。這里研究重點在第二個方面。
最早的研究人員使用RSSI加三邊測量法的定位技術,如文獻中的RADAR室內定位系統。
文獻的作者提出采用交疊環定位的方式,利用包含未知節點的相互交疊的環形區域來定位未知節點。該方法只是比較相應RSSI的大小,并未利用它測距。文獻提出一種加權質心定位算法,它提出信標節點影響力的概念,節點到信號源的距離越近,由RSSI值的偏差產生的絕對距離誤差越小,影響力越大。影響力越大的信標節點對節點位置有更大的決定權。其采用優選信標節點的方式,根據信標節點對未知節點的不同影響力確定加權因子,以此來提高定位精度。
文獻提出綜合RSSI算法和切圓圓心法的RCM算法,提高了定位精度,仿真表明,在RSSI測距誤差散布達到50%時,定位誤差可降到10%以內。
2 、基于RSSI的三角形質心算法模型
與文獻一樣,該算法針對大規模隨機散布野外應用環境,這類應用大都不需要節點進行精確定位,只需要知道節點的大概區域就可滿足需求,同時要求硬件成本低、定位過程通信開銷小、節能。
2.1 基于RSSI的定位
RSSI測量,一般利用信號傳播的經驗模型與理論模型。
對于經驗模型,在實際定位前,先選取若干測試點,記錄在這些點各基站收到的信號強度,建立各個點上的位置和信號強度關系的離線數據庫(x,y,ss1,ss2,ss3)。在實際定位時,根據測得的信號強度(ss1′,ss2′,ss3′)和數據庫中記錄的信號強度進行比較,信號強度均方差最小的那個點的坐標作為節點的坐標。
對于理論模型,常采用無線電傳播路徑損耗模型進行分析。常用的傳播路徑損耗模型有:自由空間傳播模型、對數距離路徑損耗模型、哈它模型、對數一常態分布模型等。自由空間無線電傳播路徑損耗模型為:
式中,d為距信源的距離,單位為km;f為頻率,單位為MHz;k為路徑衰減因子。其他的模型模擬現實環境,但與現實環境還是有一定的差距。比如對數一常態分布模型,其路徑損耗的計算公式為:
式中,Xσ是平均值為O的高斯分布隨機變數,其標準差范圍為4~10;k的范圍在2~5之間。取d=1,代入式(1)可得,LOSS,即PL(d0)的值。此時各未知節點接收錨節點信號時的信號強度為:
RSSI=發射功率+天線增益一路徑損耗(PL(d))
2.2 基于RSSI的三角形質心定位算法的數學模型
不論哪種模型,計算出的接收信號強度總與實際情況下有誤差,因為實際環境的復雜性,換算出的錨節點到未知節點的距離d總是大于實際兩節點間的距離。如圖1所示,錨節點A,B,C,未知節點D,根據RSSI模型計算出的節點A和D的距離為rA;節點B和D的距離為rB;節點C和D的距離為rC。分別以A,B,C為圓心;rA,rB,rC為半徑畫圓,可得交疊區域。這里的三角形質心定位算法的基本思想是:計算三圓交疊區域的3個特征點的坐標,以這三個點為三角形的頂點,未知點即為三角形質心,如圖2所示,特征點為E,F,G,特征點E點的計算方法為:
同理,可計算出F,G,此時未知點的坐標為
由仿真得,在圖2中,實際點為D;三角形質心算法出的估計點為M;三邊測量法算出的估計點為N。可知,三角形質心算法的準確度更高。
3、 基于RSSI的三角形質心算法過程
3.1 步驟
(1)錨節點周期性向周圍廣播信息,信息中包括自身節點ID及坐標。普通節點收到該信息后,對同一錨節點的RSSI取均值。
(2)當普通節點收集到一定數量的錨節點信息時,不再接收新信息。普通節點根據RSSI從強到弱對錨節點排序,并建立RSSI值與節點到錨節點距離的映射。建立3個集合。
錨節點集合:
(3)選取RSSI值大的前幾個錨節點進行自身定位計算。
在B_set:中優先選擇RSSI值大的信標節點組合成下面的錨節點集合,這是提高定位精度的關鍵。
對錨節點集合,依次根據(3)式算出3個交點的坐標,最后由質心算法,得出未知節點坐標。
(4)對求出的未知節點坐標集合取平均,得未知節點坐標。
3.2 誤差定義
定義定位誤差為ER,假設得到的未知節點的坐標為(xm,ym),其真實位置為(x,y),則定位誤差ER為:
4、 仿 真
利用Matlab仿真工具模擬三角形質心算法,考察該算法的性能。假設在100 m×100 m的正方形區域內,36個錨節點均勻分布,未知節點70個,分別用三邊測量法和三角形質心定位算法進行仿真,仿真結果如圖3所示。由圖3可知,三角形質心算法比三邊測量法,定位精度更高,當測距誤差變大時,用三角形質心算法得出的平均定位誤差比用三邊測量法得出的小得多。
5、 結 語
在此提出了將RSSI方法和三角形質心定位算法相結合的方法,通過仿真實驗,將該算法和三邊測量算法相比較,證明了該算法的優越性。下一步將研究在錨節點數量不同時的平均定位誤差。
責任編輯:gt
-
仿真
+關注
關注
50文章
4151瀏覽量
134407 -
無線電
+關注
關注
60文章
2154瀏覽量
117073 -
測量
+關注
關注
10文章
5009瀏覽量
112134
發布評論請先 登錄
相關推薦
三角形網格球面參數化研究
三角形柵格矩形徑向線螺旋陣列天線的設計與實驗研究
基于貪心優化策略的三角形排布算法
基于FLINK窗口操作的三角形計數算法
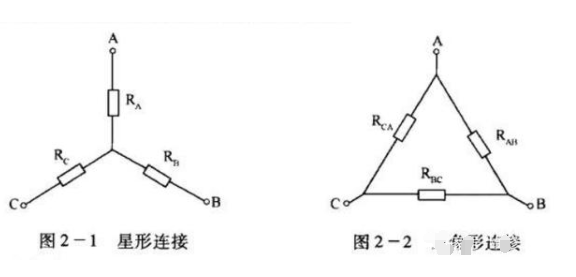
星形/三角形的變換法介紹




 基于RSSI技術的三角形質心算法的建模與仿真研究
基于RSSI技術的三角形質心算法的建模與仿真研究











評論