谷歌AI最新發布的一篇論文給出了首個關于深度神經網絡訓練相關的理論證明,實驗觀察結果也為初步解釋梯度下降強于貝葉斯優化奠定了基礎。神經網絡的理論面紗,正逐步被揭開。
原來,神經網絡實際上跟線性模型并沒那么大不同!
谷歌AI的研究人員日前在arxiv貼出一篇文章,給出了首個神經網絡訓練相關的理論證明。
實驗中,他們將一個實際的神經網絡訓練過程與線性模型的訓練過程相比,發現兩者高度一致。這里用到的神經網絡是一個wide ResNet,包括ReLU層、卷積層、pooling層和batch normalization;線性模型是用ResNet關于其初始(隨機)參數的泰勒級數建立的網絡。

將神經網絡的訓練過程與線性模型的相比,兩者高度一致
在多個不同模型上試驗并排除量化誤差后,觀察結果依舊保持一致。由此,谷歌AI研究人員得出結論,當學習率比較小且網絡足夠寬(不必無限寬)的時候,神經網絡就是線性模型。
由此得出的一個推論是,使用梯度下降訓練的大型網絡集成能夠用一個高斯過程描述,而且在梯度下降的任意時間都能用完備形式化描述這個高斯過程。
這些觀察結果也構成了一個理論框架基礎,可以用來初步解釋長期以來困擾深度學習研究界的一個難題:梯度下降究竟在哪些情況下,具體是如何優于貝葉斯優化?
在訓練深度神經網絡被戲謔為“調參煉丹”的當下,這一發現猶如一道希望的強光,射進還被排除在“科學”之外的深度學習領域,激動人心。
相關論文:使用梯度下降訓練的任意深度的Wide神經網絡與線性模型的一致性
終于,調參不再是煉丹:首個關于神經網絡訓練的理論證明
基于深度神經網絡的機器學習模型在許多任務中取得了前所未有的性能。通常,這些模型被認為是復雜系統,其中許多類型的理論分析是很棘手的。此外,由于控制優化的通常是高維的非凸損失平面(non-convex loss surfaces),因此要描述這些模型的基于梯度的訓練動態機制具有挑戰性。
就像在物理科學中常見的那樣,研究這些系統的極限通常可以解釋這些難題。對于神經網絡來說,其中一個極限就是它的“無限寬度”(infinite width),指的是完全連接層中的隱藏單元數量,或卷積層中的通道數量。
在此限制下,網絡初始化時的輸出取自高斯過程(GP);此外,在使用平方損失進行精確貝葉斯訓練后,網絡輸出仍然由GP控制。除了理論上的簡單性,nfinite-width這一限制也具有實際意義,因為許多研究已經證明,更寬的網絡可以更好地進行泛化。
在這項工作中,我們探索了梯度下降下寬的神經網絡的學習動態機制(learning dynamics),并發現動態的權重空間描述變得非常簡單:隨著寬度變大,神經網絡可以有效地被關于其初始化參數的一階泰勒展開式(first-order Taylor expansion)取代。
對于這種誘導的線性模型,梯度下降的動態機制變得易于分析了。雖然線性化只在無限寬度限制下是精確的,但我們發現,即使是有限寬度的情況下,原始網絡的預測與線性化版本的預測仍然非常一致。這種一致性在不同的架構、優化方法和損失函數之間都存在。
對于平方損失(squared loss),精確的學習動態機制允許封閉形式的解決方案,這允許我們用GP來描述預測分布的演化。這一結果可以看作是“先采樣再優化”(sample-then-optimize)后驗采樣對深度神經網絡訓練的延伸。我們的經驗模擬證實,該結果準確地模擬了具有不同隨機初始化的有限寬度模型集合中預測的變化。
谷歌AI的研究人員表示,這篇論文的幾大主要貢獻包括:
首先,我們以 Jacot et al. (2018) 最近的研究成果為基礎,該成果描述了在infinite width 限制下,整個梯度下降訓練過程中網絡輸出的精確動態。他們的結果證明了參數空間的梯度下降對應于函數空間中關于新核的核梯度下降(kernel gradient descent),即Neural Tangent Kernel (NTK)。
我們工作的一個關鍵貢獻是證明了參數空間中的動態等價于所有網絡參數、權重和偏差集合中的仿射模型的訓練動態。無論損失函數的選擇如何,這個結果都成立。在平方損失的情況下, dynamics允許一個封閉形式的解作為時間函數。
無限寬(infinitely wide)神經網絡初始化時的輸出是高斯的,并且如Jacot et al.(2018)中所述,平方損失在整個訓練過程中始終是高斯的。我們推導了該GP的均值和協方差函數的顯式時間依賴表達式,并為結果提供了新的解釋。
具體來說,該解釋對梯度下降與參數的貝葉斯后驗采樣的不同機制提供了一種定量理解:雖然這兩種方法都取自GP,但梯度下降不會從任何概率模型的后驗生成樣本。
這一觀察結果與(Matthews et al.,2017)的“先采樣后優化”(sample-then-optimize)框架形成了對比,在該框架中,只訓練頂層權重,梯度下降從貝葉斯后驗采樣。
這些觀察構成了一個框架,用來分析長期存在的問題,如梯度下降是否、如何以及在何種情況下提供了相對于貝葉斯推理的具體好處。
正如Chizat & Bach (2018b)中論述的,這些理論結果可能過于簡單,無法適用于現實的神經網絡。但是,我們通過實證研究證明了該理論在finite-width設置中的適用性,發現它準確地描述了各種條件下的學習動態機制和后驗函數分布,包括一些實際的網絡架構,如Wide Residual Network(Zagoruyko & Komodakis, 2016)。
具體實驗:無限寬的神經網絡就是線性模型
線性化網絡(linearized network)
此處,我們將考慮線性化網絡的訓練動態,具體地說,就是用一階泰勒展開代替神經網絡的輸出:
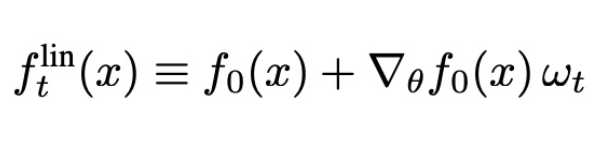
值得注意的是,flint是兩項之和:第一項是網絡的初始輸出,在訓練過程中保持不變;第二項是在訓練過程中捕捉對初始值的變化。
使用這個線性化函數的梯度流的動態受到如下約束:
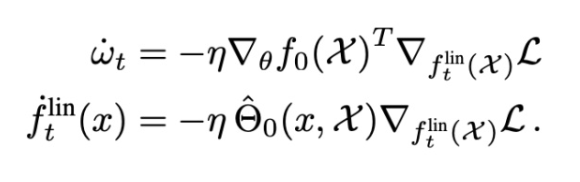
無限寬度限制產生高斯過程
當隱藏層的寬度接近無窮大時,中心極限定理(CLT)意味著初始化{f0(x)}x∈X時的輸出在分布上收斂于多元高斯分布。這一點可以用歸納法非正式的進行證明。
因此,隨機初始化的神經網絡對應于一類高斯過程(以下簡稱NNGP),將有利于神經網絡的完全貝葉斯處理。
梯度下降訓練中的高斯過程
如果我們在初始化之后凍結變量θ≤L,并且只優化θ≤L+1,那么原始網絡及其線性化是相同的。讓寬度趨于無窮,這個特殊的tangent kernel的概率將收斂于K。這是用于評估高斯過程后驗的“先采樣后優化”方法的實現。
我們對比了NNGP、NTK-GP和NN集合的預測分布,如下圖所示:
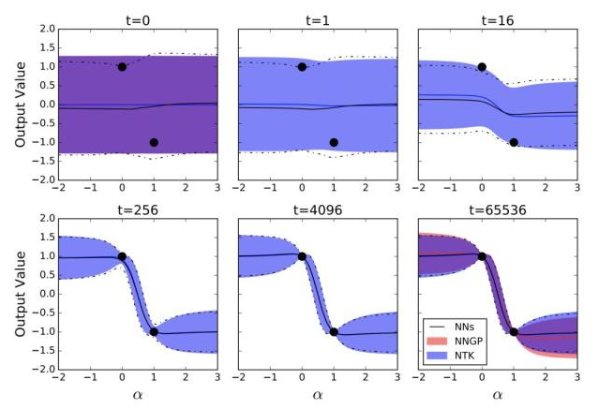
訓練神經網絡輸出的均值和方差的動態遵循線性化的分析動態機制
黑線表示來自100個訓練神經網絡集合的預測輸出分布的時間演變; 藍色區域表示整個訓練中輸出分布的分析預測;最后,紅色區域表示僅訓練頂層的預測,對應于NNGP。
受過訓練的網絡有3個隱藏層,寬度為8192。陰影區域和虛線表示平均值的2個標準偏差。
無限寬度網絡是線性化網絡
原始網絡的常微分方程(ODE)在一般情況下是不可解的。在積分函數梯度范數保持隨機有界為n1,n2,…,nL→∞的技術假設下:
值得注意的是,上面公式中的上界只是理論性的,是根據經驗觀察得到的:
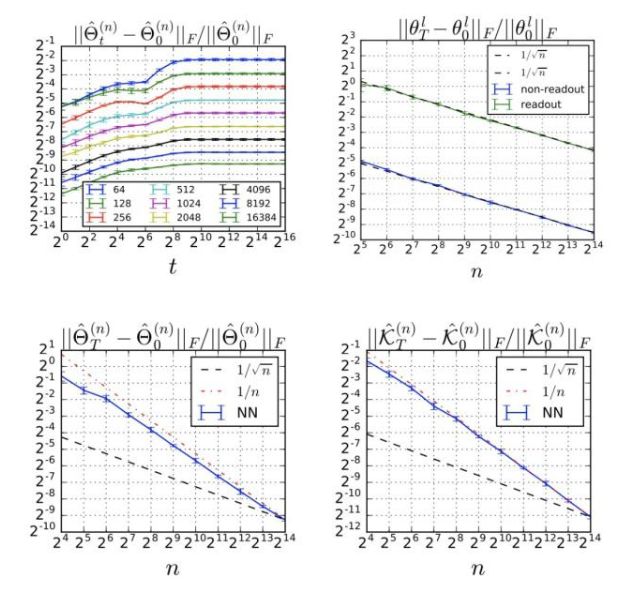
訓練過程中Relative Frobenius范數的改變
在MSE設置中,我們可以對原始網絡的輸出與其線性化輸出之間的差異進行上限:
對于非常寬的網絡,我們可以用線性化動態機制來近似訓練動態機制。
而從網絡線性化中獲得的另一個見解是,動態機制等效于隨機特征法,其中,特征是模型相對于其權重的梯度。
-
神經網絡
+關注
關注
42文章
4776瀏覽量
100945 -
梯度
+關注
關注
0文章
30瀏覽量
10333 -
機器學習
+關注
關注
66文章
8428瀏覽量
132834
發布評論請先 登錄
相關推薦




 首個關于深度神經網絡訓練相關的理論證明
首個關于深度神經網絡訓練相關的理論證明










評論