最近,「區(qū)塊鏈」、「聯(lián)邦學(xué)習(xí)」等概念受到了空前的關(guān)注。而在這些概念背后,少不了一項(xiàng)技術(shù)的影子——「同態(tài)加密」。本文介紹了使用 Julia 語(yǔ)言進(jìn)行基于同態(tài)加密數(shù)據(jù)機(jī)器學(xué)習(xí)的全過(guò)程,對(duì)于入門者具有極大的參考價(jià)值。
注意:本文討論了最前沿的密碼學(xué)技術(shù),旨在提供一種利用「Julia Computing」進(jìn)行研究的視角。請(qǐng)不要將文中的任何示例用于生產(chǎn)應(yīng)用程序。在使用密碼學(xué)之前一定要咨詢專業(yè)的密碼學(xué)專家。
引言
假設(shè)你開發(fā)了一個(gè)酷炫的新機(jī)器學(xué)習(xí)模型,現(xiàn)在你想將部署該模型,為用戶提供服務(wù)。應(yīng)該怎么做呢?最簡(jiǎn)單的方法可能是直接把模型發(fā)布給用戶,然后讓他們使用自己的數(shù)據(jù)在本地運(yùn)行這個(gè)模型。但這種方法存在一些問(wèn)題:
機(jī)器學(xué)習(xí)模型一般都很大,而用戶的設(shè)備實(shí)際上可能沒有足夠的存儲(chǔ)空間或算力來(lái)運(yùn)行模型機(jī)器學(xué)習(xí)模型一般都會(huì)頻繁地更新,你可能不會(huì)想在網(wǎng)絡(luò)上頻繁傳輸這么大的模型開發(fā)機(jī)器學(xué)習(xí)模型需要大量時(shí)間和計(jì)算資源,你可能會(huì)想通過(guò)向使用該模型的用戶收費(fèi)來(lái)收回成本
接下來(lái),常用的解決方案是將模型作為應(yīng)用程序接口(API)在云上公開。在過(guò)去幾年間,這些「機(jī)器學(xué)習(xí)即服務(wù)」產(chǎn)品如雨后春筍般涌現(xiàn),每個(gè)主要的云平臺(tái)都會(huì)為企業(yè)級(jí)開發(fā)者提供這樣的服務(wù)。
但這類產(chǎn)品的潛在用戶所面對(duì)的困境也是顯而易見的——處理用戶數(shù)據(jù)的遠(yuǎn)程服務(wù)器可能并不可信。這樣就會(huì)存在明確的倫理和法律的分歧,從而限制這種解決方案的有效范圍。在受監(jiān)管的產(chǎn)業(yè)(尤其是醫(yī)療業(yè)和金融業(yè))中,一般是不允許將病患或金融數(shù)據(jù)發(fā)送給第三方進(jìn)行處理的。我們可以做得更好嗎?
事實(shí)證明,我們可以!最近,密碼學(xué)方面取得的突破可以在無(wú)需進(jìn)行解密的情況下,直接計(jì)算加密數(shù)據(jù)。在我們的例子中,用戶可以將加密數(shù)據(jù)(例如圖像)傳遞給云 API,以此運(yùn)行機(jī)器學(xué)習(xí)模型,并返回加密的答案。整個(gè)過(guò)程中都沒有解密用戶數(shù)據(jù),尤其是云服務(wù)商既不能訪問(wèn)原始圖像,也不能解碼計(jì)算得到的預(yù)測(cè)值。這是怎么做到的呢?本文通過(guò)構(gòu)建一個(gè)進(jìn)行加密圖像的手寫識(shí)別(來(lái)自 MNIST 數(shù)據(jù)集)的機(jī)器學(xué)習(xí)模型為大家揭秘背后的原理。
同態(tài)加密(Homomorphic Encryption,HE)的一般解釋
一般而言,對(duì)加密數(shù)據(jù)進(jìn)行計(jì)算的能力被稱為「安全計(jì)算」,這是一個(gè)相當(dāng)大的研究領(lǐng)域,針對(duì)大量不同的場(chǎng)景要用不同的密碼學(xué)方法和技術(shù)解決問(wèn)題。在本例中,我們將關(guān)注所謂的「同態(tài)加密」技術(shù)。在同態(tài)加密系統(tǒng)中,我們一般要進(jìn)行以下操作:
pub_key, eval_key, priv_key = keygen()encrypted = encrypt(pub_key, plaintext)decrypted = decrypt(priv_key, encrypted)encrypted′ = eval(eval_key, f, encrypted)
前三步非常直觀,之前使用過(guò)任何非對(duì)稱加密技術(shù)的人都會(huì)對(duì)此感到很熟悉(就像通過(guò)安全傳輸層協(xié)議(TLS)連接到本文)。最后一步才是神奇之處。它使用加密數(shù)據(jù)評(píng)估了 f,并返回了另一個(gè)與基于加密值評(píng)估 f 的結(jié)果對(duì)應(yīng)的加密值。這一性質(zhì)正是我們將這種技術(shù)稱為「同態(tài)加密」的原因。評(píng)估操作與下面的加密操作等價(jià):
f(decrypt(priv_key, encrypted)) == decrypt(priv_key, eval(eval_key, f, encrypted))
(同樣地,可以基于加密值評(píng)估任意的同態(tài) f)
支持哪些函數(shù) f 取決于加密方案和支持的運(yùn)算。如果只支持一種函數(shù) f(比如 f=+),我們可以將這種加密方案稱為「部分同態(tài)」。如果 f 是可以建立任意電路的完整的門的集合,如果電路大小有限,稱之為「有限同態(tài)」(Somewhat Homomorphic Encryption, SHE);如果電路大小不受限制,稱之為「全同態(tài)」(Fully Homomorphic Encryption, FHE)。一般可以通過(guò)自助法(bootstrapping),將「有限」同態(tài)轉(zhuǎn)換為「全」同態(tài),但這個(gè)問(wèn)題已經(jīng)超過(guò)了本文所討論的內(nèi)容。
全同態(tài)加密是最近的研究,Craig Gentry 在 2009 年發(fā)表了第一個(gè)可行(但不實(shí)際)的方。現(xiàn)在陸續(xù)出現(xiàn)了一些更新也更實(shí)際的 FHE 方案。更重要的是,還有一些可以高效地實(shí)現(xiàn)這一方案的軟件包。最常用的兩個(gè)軟件包是 Microsoft SEAL和 PALISADE。此外,我最近還開源了這些算法的 Julia 實(shí)現(xiàn)(https://github.com/JuliaComputing/ToyFHE.jl)。出于我們的目的,我們將使用后者中實(shí)現(xiàn)的 CKKS 加密。
高級(jí) CKKS
CKKS(以 Cheon-Kim-Kim-Song 的名字命名,他在 2016 年的論文「Homomorphic Encryption for Arithmetic of Approximate Numbers」提出)是一種同態(tài)加密方案,可以對(duì)以下基本操作進(jìn)行同態(tài)評(píng)估:
長(zhǎng)度為 n 的復(fù)數(shù)向量的對(duì)應(yīng)元素相加長(zhǎng)度為 n 的復(fù)數(shù)向量的對(duì)應(yīng)元素相乘向量中元素的旋轉(zhuǎn)(通過(guò)循環(huán)移位實(shí)現(xiàn))向量元素的復(fù)共軛
這里的參數(shù) n 取決于需要的安全性和準(zhǔn)確性,該值一般都比較高。在本例中,n=4096(值越高越安全,但是計(jì)算開銷也更大,時(shí)間復(fù)雜度大致會(huì)縮放為 nlog^n)。
此外,用 CKKS 計(jì)算是有噪聲的。因此,計(jì)算結(jié)果一般都只是近似值,而且要注意確保評(píng)估結(jié)果足夠準(zhǔn)確,不會(huì)影響結(jié)果的正確性。
也就是說(shuō),對(duì)機(jī)器學(xué)習(xí)程序包的開發(fā)者而言,這些限制并不罕見。像 GPU 這樣有特殊用途的加速器,也可以處理數(shù)字向量。同樣,許多開發(fā)者會(huì)因算法選擇的影響、多線程等原因,認(rèn)為浮點(diǎn)數(shù)噪聲太多(我要強(qiáng)調(diào)的是,有一個(gè)關(guān)鍵的區(qū)別是,浮點(diǎn)算法本身是確定性的,盡管因?yàn)閷?shí)現(xiàn)的復(fù)雜性,它有時(shí)不會(huì)展現(xiàn)出這種確定性,但 CKKS 原語(yǔ)的噪聲真的很多,但這也許可以讓用戶意識(shí)到噪聲并沒有第一次出現(xiàn)時(shí)那么可怕)。
考慮到這一點(diǎn),我們?cè)倏纯慈绾卧?Julia 中執(zhí)行這些運(yùn)算(注意:這里有一些非常不安全的參數(shù)選擇,這些操作的目的是說(shuō)明這個(gè)庫(kù)在交互式解釋器(REPL)中的用法)。
julia》 using ToyFHE# Let‘s play with 8 element vectorsjulia》 N = 8;# Choose some parameters - we’ll talk about it laterjulia》 = NegacyclicRing(2N, (40, 40, *40*))/(x + 1)# We‘ll use CKKS julia》 params = CKKSParams()CKKS parameters# We need to pick a scaling factor for a numbers - again we’ll talk about that laterjulia》 Tscale = FixedRational{2^40}FixedRational{1099511627776,T} where T# Let‘s start with a plain Vector of zerosjulia》 plain = CKKSEncoding{Tscale}(zero())8-element CKKSEncoding{FixedRational{1099511627776,T} where T} with indices 0:7:0.0 + 0.0im0.0 + 0.0im0.0 + 0.0im0.0 + 0.0im0.0 + 0.0im0.0 + 0.0im0.0 + 0.0im0.0 + 0.0im# Ok, we’re ready to get started, but first we‘ll need some keysjulia》 kp = keygen(params)CKKS key pairjulia》 kp.privCKKS private keyjulia》 kp.pubCKKS public key# Alright, let’s encrypt some things:julia》 foreach(i-》plain[i] = i+1, 0:7); plain8-element CKKSEncoding{FixedRational{1099511627776,T} where T} with indices 0:7:1.0 + 0.0im2.0 + 0.0im3.0 + 0.0im4.0 + 0.0im5.0 + 0.0im6.0 + 0.0im7.0 + 0.0im8.0 + 0.0imjulia》 c = encrypt(kp.pub, plain)CKKS ciphertext (length 2, encoding CKKSEncoding{FixedRational{1099511627776,T} where T})
# And decrypt it againjulia》 decrypt(kp.priv, c)8-element CKKSEncoding{FixedRational{1099511627776,T} where T} with indices 0:7:0.9999999999995506 - 2.7335193113350057e-16im1.9999999999989408 - 3.885780586188048e-16im3.000000000000205 + 1.6772825551165524e-16im4.000000000000538 - 3.885780586188048e-16im4.999999999998865 + 8.382500573679615e-17im6.000000000000185 + 4.996003610813204e-16im7.000000000001043 - 2.0024593503998215e-16im8.000000000000673 + 4.996003610813204e-16im# Note that we had some noise. Let‘s go through all the primitive operations we’ll need:julia》 decrypt(kp.priv, c+c)8-element CKKSEncoding{FixedRational{1099511627776,T} where T} with indices 0:7:1.9999999999991012 - 5.467038622670011e-16im3.9999999999978817 - 7.771561172376096e-16im6.00000000000041 + 3.354565110233105e-16im8.000000000001076 - 7.771561172376096e-16im9.99999999999773 + 1.676500114735923e-16im12.00000000000037 + 9.992007221626409e-16im14.000000000002085 - 4.004918700799643e-16im16.000000000001346 + 9.992007221626409e-16imjulia》 csq = c*cCKKS ciphertext (length 3, encoding CKKSEncoding{FixedRational{1208925819614629174706176,T} where T})julia》 decrypt(kp.priv, csq)8-element CKKSEncoding{FixedRational{1208925819614629174706176,T} where T} with indices 0:7:0.9999999999991012 - 2.350516767363621e-15im3.9999999999957616 - 5.773159728050814e-15im9.000000000001226 - 2.534464540987068e-15im16.000000000004306 - 2.220446049250313e-15im24.99999999998865 + 2.0903753311370056e-15im36.00000000000222 + 4.884981308350689e-15im49.000000000014595 + 1.0182491378134327e-15im64.00000000001077 + 4.884981308350689e-15im
這很簡(jiǎn)單!敏銳的讀者可能已經(jīng)注意到了 csq 和之前的密文看起來(lái)有點(diǎn)不同。尤其是,它是「長(zhǎng)度為 3」的密文,范圍也更大。要說(shuō)明它們是什么,以及它們是做什么用的有點(diǎn)太過(guò)復(fù)雜。我只想說(shuō),在進(jìn)一步計(jì)算之前,我們要得讓這些值降下來(lái),否則我們會(huì)盡密文中的「空間」。幸運(yùn)的是,有一種方法可以解決這兩個(gè)問(wèn)題:
# To get back down to length 2, we need to `keyswitch` (aka# relinerarize), which requires an evaluation key. Generating# this requires the private key. In a real application we would# have generated this up front and sent it along with the encrypted# data, but since we have the private key, we can just do it now.julia》 ek = keygen(EvalMultKey, kp.priv)CKKS multiplication keyjulia》 csq_length2 = keyswitch(ek, csq)CKKS ciphertext (length 2, encoding CKKSEncoding{FixedRational{1208925819614629174706176,T} where T})
# Getting the scale back down is done using modswitching.julia》 csq_smaller = modswitch(csq_length2)CKKS ciphertext (length 2, encoding CKKSEncoding{FixedRational{1.099511626783e12,T} where T})
# And it still decrypts correctly (though note we‘ve lost some precision)julia》 decrypt(kp.priv, csq_smaller)8-element CKKSEncoding{FixedRational{1.099511626783e12,T} where T} with indices 0:7:0.9999999999802469 - 5.005163520332181e-11im3.9999999999957723 - 1.0468514951188039e-11im8.999999999998249 - 4.7588542623100616e-12im16.000000000023014 - 1.0413447889166631e-11im24.999999999955193 - 6.187833723406491e-12im36.000000000002345 + 1.860733715346631e-13im49.00000000001647 - 1.442396043149794e-12im63.999999999988695 - 1.0722489563648028e-10im
此外,modswitching(模轉(zhuǎn)換:modulus switching 的簡(jiǎn)寫)減少了密文模的大小,所以我們不能無(wú)限地這么做下去。(用上文提到的術(shù)語(yǔ)來(lái)說(shuō),我們?cè)谶@里使用的是 SHE 方案):
julia》 # Remember the ring we initially created/(x + 1)julia》 ToyFHE.ring(csq_smaller) # It shrunk!/(x + 1)
我們要做的最后一步運(yùn)算是:旋轉(zhuǎn)。就像上文的密鑰轉(zhuǎn)換(KeySwitching),在這里也需要評(píng)估密鑰(也稱為伽羅瓦(galois)密鑰):
julia》 gk = keygen(GaloisKey, kp.priv; steps=2)CKKS galois key (element 25)julia》 decrypt(circshift(c, gk))decrypt(kp, circshift(c, gk))8-element CKKSEncoding{FixedRational{1099511627776,T} where T} with indices 0:7:7.000000000001042 + 5.68459112632516e-16im8.000000000000673 + 5.551115123125783e-17im0.999999999999551 - 2.308655353580721e-16im1.9999999999989408 + 2.7755575615628914e-16im3.000000000000205 - 6.009767921608429e-16im4.000000000000538 + 5.551115123125783e-17im4.999999999998865 + 4.133860996136768e-17im6.000000000000185 - 1.6653345369377348e-16im# And let’s compare to doing the same on the plaintextjulia》 circshift(plain, 2)8-element OffsetArray(::Array{Complex{Float64},1}, 0:7) with eltype Complex{Float64} with indices 0:7:7.0 + 0.0im8.0 + 0.0im1.0 + 0.0im2.0 + 0.0im3.0 + 0.0im4.0 + 0.0im5.0 + 0.0im6.0 + 0.0im
好了,我們已經(jīng)了解了同態(tài)加密庫(kù)的基本用法。在思考如何用這些原語(yǔ)進(jìn)行神經(jīng)網(wǎng)絡(luò)推斷之前,我們先觀察并訓(xùn)練我們需要使用的神經(jīng)網(wǎng)絡(luò)。
機(jī)器學(xué)習(xí)模型
如果你不熟悉機(jī)器學(xué)習(xí)或 Flux.jl 機(jī)器學(xué)習(xí)庫(kù),我建議你先快速閱讀一下 Flux.jl 文檔或我們?cè)?JuliaAcademy 上發(fā)布的免費(fèi)機(jī)器學(xué)習(xí)介紹課程,因?yàn)槲覀冎粫?huì)討論在加密數(shù)據(jù)上運(yùn)行模型所做的更改。
我們將以 Flux 模型空間中卷積神經(jīng)網(wǎng)絡(luò)的例子為出發(fā)點(diǎn)。在這個(gè)模型中,訓(xùn)練循環(huán)、數(shù)據(jù)預(yù)處理等操作都不變,只是輕微地調(diào)整模型。我們要用的模型是:
functionreshape_and_vcat(x) lety=reshape(x, 64, 4, size(x, 4)) vcat((y[:,i,:] for i=axes(y,2))。..) endendmodel = Chain( # First convolution, operating upon a 28x28 image Conv((7, 7), 1=》4, stride=(3,3), x-》x.^2), reshape_and_vcat, Dense(256, 64, x-》x.^2), Dense(64, 10),)
該模型與「安全外包矩陣的計(jì)算及其在神經(jīng)網(wǎng)絡(luò)上與應(yīng)用」(Secure Outsourced Matrix Computation and Application to Neural Networks)文中所用的模型基本相同,它們用相同的加密方案演示了相同的模型,但有兩個(gè)區(qū)別:(1)他們加密了模型而我們(為簡(jiǎn)單起見)沒有對(duì)模型加密;(2)我們?cè)诿恳粚又蠖加衅孟蛄浚ㄟ@也是 Flux 的默認(rèn)行為),我不確定這種行為對(duì)本文評(píng)估的模型是否是這樣。也許是因?yàn)椋?),我們模型的準(zhǔn)確率才略高(98.6% vs 98.1%),但這也可能僅僅是因?yàn)槌瑓?shù)的差異。
「x.^2」激活函數(shù)也是一個(gè)不尋常的特征(對(duì)那些有機(jī)器學(xué)習(xí)背景的人來(lái)說(shuō))。這里更常用的選擇可能是「tanh」、「relu」或者其他更高級(jí)的函數(shù)。然而,盡管這些函數(shù)(尤其是 relu)可以更容易地評(píng)估明文值,但評(píng)估加密數(shù)據(jù)的計(jì)算開銷則相當(dāng)大(基本上是評(píng)估多項(xiàng)式近似值)。幸運(yùn)的是,「x.^2」可以很好地滿足我們的目的。
其余的訓(xùn)練循環(huán)基本上是相同的。我們從模型中刪除了「softmax」,取而代之的是「logitcrossentropy」損失函數(shù)(當(dāng)然也可以保留它,在客戶端解密后再評(píng)估「softmax」)。訓(xùn)練模型的完整代碼見 GitHub,在近期發(fā)布的 GPU 上只需要幾分鐘就可以完成訓(xùn)練。
代碼地址:https://github.com/JuliaComputing/ToyFHE.jl/blob/master/examples/encrypted_mnist/train.jl
高效地計(jì)算
好了,現(xiàn)在已經(jīng)明確了我們需要做什么,接下來(lái)看看我們要做哪些運(yùn)算:
卷積 元素平方 矩陣乘法
我們?cè)谏衔闹幸呀?jīng)看到了,元素平方操作是很簡(jiǎn)單的,所以我們按順序處理剩下的兩個(gè)問(wèn)題。在整個(gè)過(guò)程中,假設(shè)批處理大小(batch size)為 64(你可能注意到了,我們有策略地選擇模型參數(shù)和批處理大小,從而充分利用 4096 元素向量的優(yōu)勢(shì),這是我們從實(shí)際的參數(shù)選擇中得到的)。
卷積
讓我們回顧一下卷積是如何工作的。首先,取原始輸入數(shù)組中的一些窗口(本例中為 7*7),窗口中的每個(gè)元素跟卷積掩模的元素相乘。然后移動(dòng)窗口(本例中步長(zhǎng)為 3,所以將窗口移動(dòng) 3 個(gè)元素)。重復(fù)這個(gè)過(guò)程(用相同的卷積掩模)。下面的動(dòng)畫說(shuō)明了以(2,2)的步長(zhǎng)進(jìn)行 3*3 卷積的過(guò)程(藍(lán)色數(shù)組是輸入,綠色數(shù)組是輸出)。
另外,我們將卷積分成 4 個(gè)不同的「通道」(這意味著用不同的卷積掩模,將卷積又重復(fù)了 3 次)
好了,現(xiàn)在我們已經(jīng)知道了要做什么,接下來(lái)考慮一下該如何實(shí)現(xiàn)。幸運(yùn)的是,卷積是我們模型中的第一步運(yùn)算。因此,可以在加密數(shù)據(jù)之前(無(wú)需模型權(quán)重)先在客戶端上預(yù)處理,來(lái)節(jié)省一些工作。具體而言,我們將執(zhí)行以下操作:
預(yù)先計(jì)算每個(gè)卷積窗口(即從原始圖像中提取 7*7 的窗口),從每個(gè)輸入圖像中得到 64 個(gè) 7*7 的矩陣(注意要在步長(zhǎng)為 2 的情況下得到 7*7 的窗口,要評(píng)估 28*28 的輸入圖像的話,要計(jì)算 8*8 的卷積窗口) 將每個(gè)窗口中的相同位置收集到一個(gè)向量中,即對(duì)每張圖來(lái)說(shuō),都會(huì)有包含 64 個(gè)元素的向量,或當(dāng)批處理大小為 64 時(shí),會(huì)得到 64*64 的元素向量(即,共有 49 個(gè) 64*64 的矩陣) 加密
然后卷積就變成了整個(gè)矩陣和適當(dāng)掩碼元素的標(biāo)量乘法,對(duì)這 49 個(gè)元素求和,得到了卷積的結(jié)果。這個(gè)方案是這樣實(shí)現(xiàn)的(在明文上):
function public_preprocess(batch) ka = OffsetArray(0:7, 0:7) # Create feature extracted matrix I = [[batch[i′*3 .+ (1:7), j′*3 .+ (1:7), 1, k] for i′=ka, j′=ka] for k = 1:64] # Reshape into the ciphertext I = [[I[k][l.。.][i,j] for k=1:64, l=product(ka, ka)] for i=1:7, j=1:7]endI = public_preprocess(batch)# Evaluate the convolutionweights = model.layers[1].weightconv_weights = reverse(reverse(weights, dims=1), dims=2)conved = [sum(I[i,j]*conv_weights[i,j,1,channel] for i=1:7, j=1:7) for channel = 1:4]conved = map(((x,b),)-》x .+ b, zip(conved, model.layers[1].bias))
這樣的實(shí)現(xiàn)(對(duì)維度重新排序的模)給出了相同的答案,但是用了這樣的操作:
model*.*layers[*1*](batch)
加入加密操作后,我們得到:
I = public_preprocess(batch)C_I = map(I) do Iij plain = CKKSEncoding{Tscale}(zero(plaintext_space(ckks_params))) plain 。= OffsetArray(vec(Iij), 0:(N÷2-1)) encrypt(kp, plain)endweights = model.layers[1].weightconv_weights = reverse(reverse(weights, dims=1), dims=2)conved3 = [sum(C_I[i,j]*conv_weights[i,j,1,channel] for i=1:7, j=1:7) for channel = 1:4]conved2 = map(((x,b),)-》x .+ b, zip(conved3, model.layers[1].bias))conved1 = map(ToyFHE.modswitch, conved2)
注意,由于權(quán)重是公開的,所以不需要密鑰轉(zhuǎn)換,因此沒有擴(kuò)展密文的長(zhǎng)度。
矩陣乘法
接下來(lái)看看矩陣乘法是如何實(shí)現(xiàn)的。我們利用這樣的事實(shí)——可以旋轉(zhuǎn)向量中的元素,來(lái)重排序乘法索引。特別是,要考慮向量中矩陣元素的行優(yōu)先排序。然后,如果以行大小的倍數(shù)移動(dòng)向量,就可以得到列旋轉(zhuǎn)的效果,這可以提供充足的原語(yǔ)來(lái)實(shí)現(xiàn)矩陣乘法(至少是方陣)。我們不妨試一下:
function matmul_square_reordered(weights, x) sum(1:size(weights, 1)) do k # We rotate the columns of the LHS and take the diagonal weight_diag = diag(circshift(weights, (0,(k-1)))) # We rotate the rows of the RHS x_rotated = circshift(x, (k-1,0)) # We do an elementwise, broadcast multiply weight_diag .* x_rotatedendendfunction matmul_reorderd(weights, x) sum(partition(1:256, 64)) dorange matmul_square_reordered(weights[:, range], x[range, :]) endendfc1_weights = model.layers[3].Wx = rand(Float64, 256, 64)@assert (fc1_weights*x) ≈ matmul_reorderd(fc1_weights, x)
當(dāng)然,對(duì)于一般的矩陣乘法,我們可能需要更好的方法,但是在本例中,現(xiàn)在這種程度就已經(jīng)足夠了。
優(yōu)化代碼
至此,我們?cè)O(shè)法將所有內(nèi)容整合在一起,而且也確實(shí)奏效了。這里提供了代碼作為參考(省略了參數(shù)選擇等設(shè)置):
ek = keygen(EvalMultKey, kp.priv)gk = keygen(GaloisKey, kp.priv; steps=64)I = public_preprocess(batch)C_I = map(I) do Iij plain = CKKSEncoding{Tscale}(zero(plaintext_space(ckks_params))) plain 。= OffsetArray(vec(Iij), 0:(N÷2-1)) encrypt(kp, plain)endweights = model.layers[1].weightconv_weights = reverse(reverse(weights, dims=1), dims=2)conved3 = [sum(C_I[i,j]*conv_weights[i,j,1,channel] for i=1:7, j=1:7) for channel = 1:4]conved2 = map(((x,b),)-》x .+ b, zip(conved3, model.layers[1].bias))conved1 = map(ToyFHE.modswitch, conved2)Csqed1 = map(x-》x*x, conved1)Csqed1 = map(x-》keyswitch(ek, x), Csqed1)Csqed1 = map(ToyFHE.modswitch, Csqed1)function encrypted_matmul(gk, weights, x::ToyFHE.CipherText) result = repeat(diag(weights), inner=64).*x rotated = x for k = 2:64 rotated = ToyFHE.rotate(gk, rotated) result += repeat(diag(circshift(weights, (0,(k-1)))), inner=64) .* rotated end resultendfq1_weights = model.layers[3].WCfq1 = sum(enumerate(partition(1:256, 64))) do (i,range) encrypted_matmul(gk, fq1_weights[:, range], Csqed1[i])endCfq1 = Cfq1 .+ OffsetArray(repeat(model.layers[3].b, inner=64), 0:4095)Cfq1 = modswitch(Cfq1)Csqed2 = Cfq1*Cfq1Csqed2 = keyswitch(ek, Csqed2)Csqed2 = modswitch(Csqed2)function naive_rectangular_matmul(gk, weights, x) @assert size(weights, 1) 《 size(weights, 2) weights = vcat(weights, zeros(eltype(weights), size(weights, 2)-size(weights, 1), size(weights, 2))) encrypted_matmul(gk, weights, x)endfq2_weights = model.layers[4].WCresult = naive_rectangular_matmul(gk, fq2_weights, Csqed2)Cresult = Cresult .+ OffsetArray(repeat(vcat(model.layers[4].b, zeros(54)), inner=64), 0:4095)
雖然代碼看起來(lái)不是很清晰,但是如果你已經(jīng)進(jìn)行到這一步了,那你就應(yīng)該理解這個(gè)流程中的每一步。
現(xiàn)在,把注意力轉(zhuǎn)移到可以讓這一切更好理解的抽象上。我們先跳出密碼學(xué)和機(jī)器學(xué)習(xí)領(lǐng)域,考慮編程語(yǔ)言設(shè)計(jì)的問(wèn)題。Julia 可以實(shí)現(xiàn)強(qiáng)大的抽象,我們可以利用這一點(diǎn)構(gòu)建一些抽象。例如,可以將整個(gè)卷積提取過(guò)程封裝為自定義數(shù)組類型:
using BlockArrays“”“ ExplodedConvArray{T, Dims, Storage} 《: AbstractArray{T, 4}Represents a an `nxmx1xb` array of images, but rearranged into aseries of convolution windows. Evaluating a convolution compatiblewith `Dims` on this array is achievable through a sequence ofscalar multiplications and sums on the underling storage.”“”struct ExplodedConvArray{T, Dims, Storage} 《: AbstractArray{T, 4} # sx*sy matrix of b*(dx*dy) matrices of extracted elements # where (sx, sy) = kernel_size(Dims) # (dx, dy)=output_size(DenseConvDims(。..)) cdims::Dims x::Matrix{Storage} function ExplodedConvArray{T, Dims, Storage}(cdims::Dims, storage::Matrix{Storage}) where {T, Dims, Storage} @assert all(==(size(storage[1])), size.(storage)) new{T, Dims, Storage}(cdims, storage) endendBase.size(ex::ExplodedConvArray) = (NNlib.input_size(ex.cdims)。.., 1, size(ex.x[1], 1))function ExplodedConvArray{T}(cdims, batch::AbstractArray{T, 4}) where {T} x, y = NNlib.output_size(cdims) kx, ky = NNlib.kernel_size(cdims) stridex, stridey = NNlib.stride(cdims) kax = OffsetArray(0:x-1, 0:x-1) kay = OffsetArray(0:x-1, 0:x-1) I = [[batch[i′*stridex .+ (1:kx), j′*stridey .+ (1:ky), 1, k] for i′=kax, j′=kay] for k = 1:size(batch, 4)] I = [[I[k][l.。.][i,j] for k=1:size(batch, 4), l=product(kax, kay)] for (i,j) in product(1:kx, 1:ky)]
ExplodedConvArray{T, typeof(cdims), eltype(I)}(cdims, I)endfunction NNlib.conv(x::ExplodedConvArray{《:Any, Dims}, weights::AbstractArray{《:Any, 4}, cdims::Dims) where {Dims《:ConvDims} blocks = reshape([ Base.ReshapedArray(sum(x.x[i,j]*weights[i,j,1,channel] for i=1:7, j=1:7), (NNlib.output_size(cdims)。..,1,size(x, 4)), ()) for channel = 1:4 ],(1,1,4,1)) BlockArrays._BlockArray(blocks, BlockArrays.BlockSizes([8], [8], [1,1,1,1], [64]))end
注意,如原始代碼所示,這里用 BlockArrays 將 8*8*4*64 的數(shù)組表示成 4 個(gè) 8*8*1*64 的數(shù)組。所以現(xiàn)在,我們已經(jīng)得到了第一個(gè)步驟更好的表征(至少是在未加密數(shù)組上):
julia》 cdims = DenseConvDims(batch, model.layers[1].weight; stride=(3,3), padding=(0,0,0,0), dilation=(1,1))DenseConvDims: (28, 28, 1) * (7, 7) -》 (8, 8, 4), stride: (3, 3) pad: (0, 0, 0, 0), dil: (1, 1), flip: falsejulia》 a = ExplodedConvArray{eltype(batch)}(cdims, batch);julia》 model(a)10×64 Array{Float32,2}:[snip]如何將這種表征帶入加密的世界呢?我們需要做兩件事:如何將這種表征帶入加密的世界呢?我們需要做兩件事:
1. 我們想以這樣的方式加密結(jié)構(gòu)體(ExplodedConvArray),以致于對(duì)每個(gè)字段(field)都能得到一個(gè)密文。然后,通過(guò)查詢?cè)摵瘮?shù)在原始結(jié)構(gòu)上執(zhí)行的操作,在加密的結(jié)構(gòu)體上進(jìn)行運(yùn)算,并直接進(jìn)行相同的同態(tài)操作。
2. 我們希望攔截某些在加密的上下文中以不同方式執(zhí)行的操作。
幸運(yùn)的是 Julia 提供了可以同時(shí)執(zhí)行這兩個(gè)操作的抽象:使用 Cassette.jl 機(jī)制的編譯器插件。它是如何起作用的,以及如何使用它,都有些復(fù)雜,本文中不再深入介紹這部分內(nèi)容。簡(jiǎn)言之,你可以定義上下文(即「Excrypted」,然后定義在這樣的上下文中,運(yùn)算是如何起作用的規(guī)則)。例如,第二個(gè)要求可以寫成:
所有這一切的最終結(jié)果是,用戶可以以最少的手工工作,寫完整個(gè)內(nèi)容:
當(dāng)然,就算經(jīng)過(guò)了以上處理,代碼也不是最優(yōu)的。加密系統(tǒng)的參數(shù)(例如 環(huán),什么時(shí)候模轉(zhuǎn)換,什么時(shí)候密鑰轉(zhuǎn)換等)表現(xiàn)出了在答案的準(zhǔn)確性、安全性以及性能之間的取舍,而且參數(shù)很大程度上取決于正在運(yùn)行的代碼。一般來(lái)說(shuō),人們希望編譯器能分析將要運(yùn)行的加密代碼,為給定的安全等級(jí)和所需精度提出參數(shù)建議,然后用戶以最少的人工操作來(lái)生成代碼。
結(jié)語(yǔ)
對(duì)于任何系統(tǒng)來(lái)說(shuō),安全地自動(dòng)執(zhí)行任意計(jì)算都是一項(xiàng)艱巨的任務(wù),但 Julia 的元編程功能和友好的語(yǔ)法都讓它成為合適的開發(fā)平臺(tái)。RAMPARTS 系統(tǒng)已經(jīng)做了一些嘗試,將簡(jiǎn)單的 Julia 代碼編譯到 PALISADE FHE 庫(kù)中。「Julia Computing」正在與 RAMPARTS 背后的專家在 Verona 平臺(tái)上合作,最近已經(jīng)發(fā)布了下一代版本。在過(guò)去的一年中,同態(tài)加密系統(tǒng)的性能才達(dá)到能以實(shí)際可用的速度評(píng)估有趣計(jì)算的程度。一扇嶄新的大門就此打開。隨著算法、軟件和硬件的進(jìn)步,同態(tài)加密必然會(huì)成為保護(hù)數(shù)百萬(wàn)用戶隱私的主流技術(shù)。
-
模型
+關(guān)注
關(guān)注
1文章
3268瀏覽量
48937 -
機(jī)器學(xué)習(xí)
+關(guān)注
關(guān)注
66文章
8428瀏覽量
132806 -
加密數(shù)據(jù)
+關(guān)注
關(guān)注
0文章
4瀏覽量
6459
發(fā)布評(píng)論請(qǐng)先 登錄
相關(guān)推薦
自然語(yǔ)言處理與機(jī)器學(xué)習(xí)的關(guān)系 自然語(yǔ)言處理的基本概念及步驟
在學(xué)習(xí)go語(yǔ)言的過(guò)程踩過(guò)的坑
【《大語(yǔ)言模型應(yīng)用指南》閱讀體驗(yàn)】+ 基礎(chǔ)知識(shí)學(xué)習(xí)
【《大語(yǔ)言模型應(yīng)用指南》閱讀體驗(yàn)】+ 基礎(chǔ)篇
天合光能獲“全過(guò)程功率測(cè)量控制評(píng)估認(rèn)證”證書
紅豆Cat 1開源 項(xiàng)目四: 從0-1設(shè)計(jì)一款TCP版本DTU產(chǎn)品的軟硬件全過(guò)程

紅豆Cat 1開源 項(xiàng)目三: 從0-1設(shè)計(jì)一款HTTP版本RTU 支持GNSS 產(chǎn)品的軟硬件全過(guò)程
紅豆Cat 1開源 項(xiàng)目二: 從0-1設(shè)計(jì)一款MQTT版本DTU 支持GNSS 產(chǎn)品的軟硬件全過(guò)程
紅豆Cat 1開源 項(xiàng)目一: 從0-1設(shè)計(jì)一款TCP版本RTU 支持Modbus+GNSS 產(chǎn)品的軟硬件全過(guò)程
解讀PyTorch模型訓(xùn)練過(guò)程
深度學(xué)習(xí)模型訓(xùn)練過(guò)程詳解
機(jī)器學(xué)習(xí)的經(jīng)典算法與應(yīng)用

精準(zhǔn)到毫米:H9激光切管機(jī)鋁材切割與打孔全過(guò)程解析

物聯(lián)網(wǎng)與醫(yī)療廢物處置全過(guò)程電子信息化跟蹤管理系統(tǒng)研究
永磁同步電機(jī)全速域矢量控制的全過(guò)程介紹
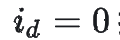




 使用Julia語(yǔ)言進(jìn)行基于同態(tài)加密數(shù)據(jù)機(jī)器學(xué)習(xí)的全過(guò)程
使用Julia語(yǔ)言進(jìn)行基于同態(tài)加密數(shù)據(jù)機(jī)器學(xué)習(xí)的全過(guò)程










評(píng)論