前言

說到正則化大家應該都不陌生，這個在機器學習和深度學習中都是非常常見的，常用的正則化有L1正則化和L2正則化。提到正則化大家就會想到是它會將權重添加到損失函數計算中來降低模型過擬合的程度。了解更多一點的同學還會說，L1正則化會讓模型的權重參數稀疏化(部分權重的值為0)，L2正則化會讓模型的權重有趨于0的偏好。

不知道大家有沒有想過為什么L1正則化會讓部分權重的值為0？為什么L2正則化會讓權重會有偏向于0？為什么正則化可以防止過擬合？正則化究竟是怎么來的？ 帶著這些問題，我們來看這篇文章，會幫助大家一一解答。

正則化的由來

在介紹正則化之前，我們先來看一張圖

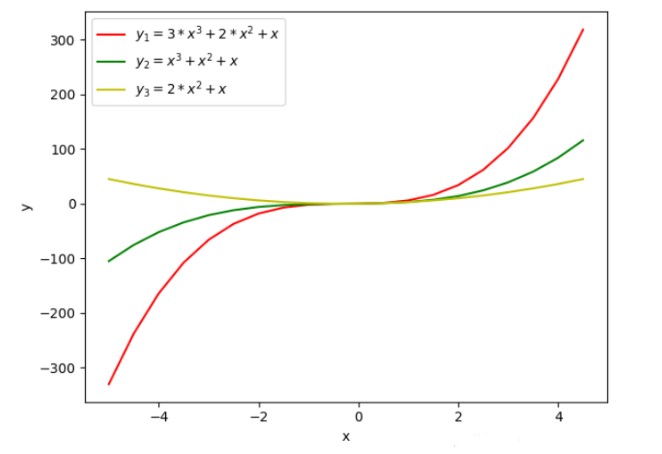
在上圖中我們繪制了三條不同的曲線y1、y2、y3 ，從曲線函數值的變化不難看出，y1的函數值變化最大，y2和y3的函數值相對來說要平緩一些。通過函數的表達式可以看出，y2 相對于y1 來說自變量的系數值變小了，y3相對y1 來說自變量少了一個，我們可以理解為少的那個自變量的系數為0。

通常如果函數的取值變化的幅度更大，我們會認為函數更復雜，函數的方差更大。所以，上面的三個函數中，函數y1的復雜度最高。通過函數圖像可以發現，降低自變量的系數值，或者減少函數自變量的個數等價于自變量的系數為0是可以降低函數復雜度的。

在構建模型之前，我們是不知道數據的分布，如果模型過于簡單就會導致欠擬合，如果模型過于復雜就會過擬合。通常我們為了模型能夠更好的擬合數據都是使得模型處于過擬合，為了降低模型的過擬合就需要使得模型部分權重為0或者降低模型的權重，所以我們會為損失函數添加一個懲罰項，數學表達式如下

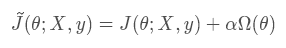
上式中的J(θ;X,y)表示原目標函數(沒有添加正則化)，Ω(θ)表示模型參數的懲罰項，懲罰項系數α∈[0,∞) ，α 越大表示正則化懲罰越大。

需要注意：我們在對模型的參數做懲罰的時候，其實只是添加了模型的權重參數并不包括偏置參數，因為模型的偏置參數數量相對于權重參數數量來說要少的多，而且每個權重參數會指定兩個變量如何相互作用，而偏置只是控制一個單一的變量，所以我們不對偏置做正則化也不會導致太大的方差。而且，如果對偏置進行正則化可能會導致明顯的欠擬合。

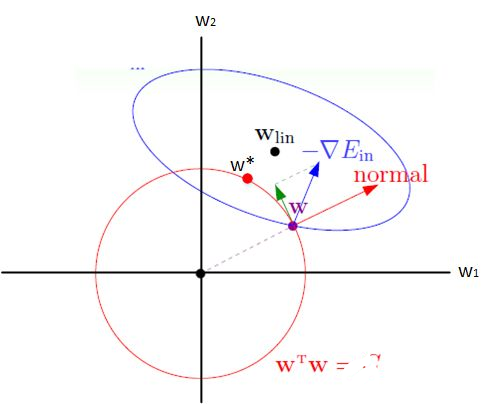
上式中的參數θ 包含了權重和偏置，而我們只需要對權重做正則化。所以，L1正則化和L2正則化可以改成如下表達式

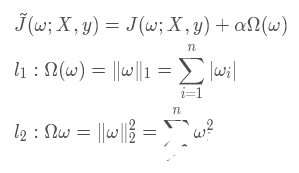
正則化的影響

在正則化的由來中，我們直觀的介紹了為什么需要加入正則化？接下來我們來介紹一下為什么l1 正則化會使得模型的部分參數為0，l2 正則化會使得模型的參數接近0。為了更好的證明，接下來的公式可能會有點多，不過我會盡可能的詳細讓大家更好的理解

1. 直觀理解

為了幫助大家從直觀上理解正則化的效果，接下來我們將通過畫圖來觀察l1正則化和l2正則化的效果

前面我們介紹了正則化其實就是在原代價函數的基礎上多增加了一項參數的懲罰項，目的就是為了不讓網絡的參數過大而導致模型過擬合，所以我們其實可以將正則化后的代價函數理解為在最小化原代價函數的基礎上多增加了一個參數的約束函數，對于約束函數的要求就是它需要小于某個常數C

l1 正則化

我們將l1 正則化效果等價于求原代價函數的最小值和對權重參數的約束函數，這里為了便于作圖我們只考慮二維情況

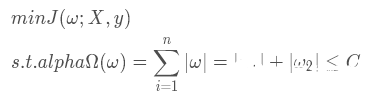
根據上兩個式子，我們可以繪制出線性規劃圖如下

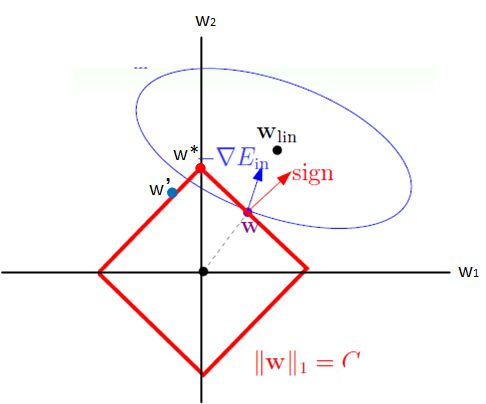
上圖中的藍色橢圓表示的是原代價函數的等高線，紅色矩形表示的是權重的約束函數，圖中的紅色箭頭表示的是約束函數的法向量方向，其中藍色箭頭表示的是原代價函數在該點的梯度方向(等高線的梯度方向與它的法向量方向一致)

因為約束函數的限制導致ω 只能在紅色矩形的邊上進行移動來尋找最佳的ω?。當ω處于上圖中的位置時，將原代價函數的梯度分解為沿約束函數的切線方向(即矩形的邊)和法線方向，為了使得原代價函數取得最小值此時需要沿著梯度在約束函數的切線方向(左上方)移動。當ω移動到ω′ 時，通過分解原代價函數的梯度可以發現，為了使得取得原代價函數的最小值應該沿著右上方移動，所以最終最優的ω? 應該為矩形的頂點位置。

通過觀察可以發現此時ω? 在坐標軸ω1 方向的取值為0，這也就是為什么l1 正則化會使得權重參數稀疏的原因。

l2 正則化

同樣，我們按照分析l1正則化的思路進行分析

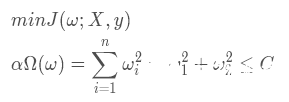
上圖中藍色橢圓表示是原代價函數的等高線，紅色圓表示的是權重的約束函數它的半徑是√ C ，其中藍色箭頭表示的是原代價函數在該點的梯度方向，紅色箭頭表示的是約束函數在該點的法向量方向，綠色箭頭表示的是約束函數在該點的切線方向。

還是按照上面的思想我們將梯度按切線方向和法線方向進行分解，為了使得原代價函數取得最小值，我們需要將ω 按切線方向進行移動，當移動到ω? 時，梯度方向與切線方向垂直時梯度沿切線方向的分量為0，此時原代價函數取得最小值，所以ω? 為最優點。

通過觀察上圖可以發現，此時ω1的取值接近于0，這也就是為什么l2正則化會使得權重趨于0的原因。

2. 公式推導證明

l2 正則化

l2 正則化也被稱為權重衰減或嶺回歸，在神經網絡中也被經常用到，因為它會使得權重向零點靠近(使得權重的取值趨于0)。為了更好的觀察l2正則化的影響，接下來我們觀察一下在添加罰項之后，權重參數是如何更新的

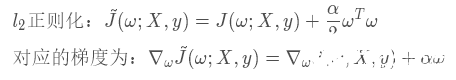
使用單步梯度下降更新權重，更新公式如下：

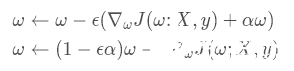
上式中的，? 指的是學習率，α 指的是權重衰減系數，這兩個參數通常都是小于1的。

通過單步的權重的梯度更新公式可以發現，權重每次在更新之前都需要乘以一個小于1的系數，相當于每次更新權重的時候都對它做了衰減，在經過多次權重更新之后會，權重的系數會接近于0，最終會導致權重也接近0，假設權重的系數為0.9，經過100次權重的迭代更新，最終權重系數會變為0.9100≈2.7?10?5(注：這里沒有考慮梯度的大小，只是簡單表明這種趨勢)。

上面只是一個單步的權重更新過程，接下來我們推導一下在整個訓練過程中，權重的更新過程，為了簡化分析我們假設ω? 為J(ω)取得最小值時的權重向量，根據泰勒公式

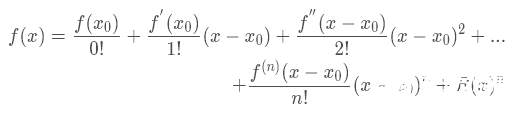
假設J(ω)二階可導，我們對其進行二次近似的泰勒展開則有

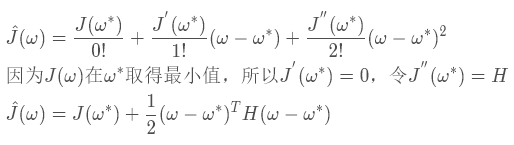
為了讓?J (ω)取得最小值，我們令其導數為0，因為?J(ω?)為常數，所以它的導數為0，我們就直接省略了

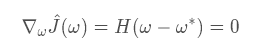
接下來我們研究添加l2 正則化之后的對?J(ω)的影響，我們假設?ω為l2正則化之后?J(ω)的最優解，可得它的導數為

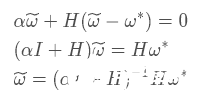
上式中的 I 表示的是單位矩陣，通過上式不難發現，當正則化的懲罰項系數α 為0時，此時?ω 的最優解就等于ω?，接下來我們討論一下當懲罰項系數不為0的時。因為H 是J 在ω? 的Hessian矩陣，所以H 是一個對稱矩陣，我們可以對其做特征分解，可得 H = QΛQT，其中Λ為對角矩陣，Q 為一組特征向量的標準正交基，代入上式可得

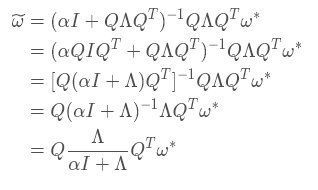
通過上面的式子可以發現，l2正則化的效果就是沿著H 矩陣特征向量所定義的軸縮放未正則化J(ω)的解ω?。因為 I 是單位矩陣，我們可以將縮放的系數改成這種形式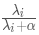?，其中λi指的是矩陣H的特征向量每個軸值的大小，也就是特征分解之后特征值的大小。

通過修改后的衰減系數不難發現，當特征值 λi>>α 時，此時α的影響可以忽略不計，正則化的縮放系數會趨于1，正則化基本沒有影響。當特征值 λi<<α 時，可以將縮放系數改為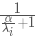，因為 α>>λi 所以 (α/λi)>>1，所以縮放系數 (λ/iα)<<1，縮放系數趨于0使得權重也會趨于0。

l1正則化

上面我們推導了添加了l2 正則化之后對權重的影響，通過最后推導得到式子可以解釋為什么l2正則化會讓權重趨于0。接下來，我們以類似的方式來推導l1正則化對于權重的影響

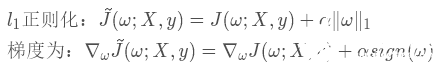
上式中的sign函數為符號函數，函數圖像如下

當函數輸入值x<0 時輸出值恒等于 -1，輸入值為0時輸出值也等于0，輸入值 x>1 時輸出值恒等于1，sign函數經常被用來表示階躍函數

我們將J(ω;X,y) 使用二階的泰勒展開式來代替，可以將l1正則化后的代價函數轉換為如下形式

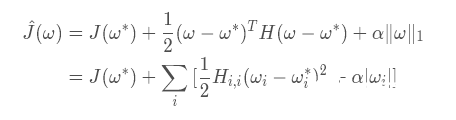
接下來我們看看如何求解ωi，上式中的J(ω?)是常數我們不用考慮，主要考慮求和式中的二次項式和絕對值式來使得整個代價函數取得最小值，為了求得后兩項和的最小值，我們對其求導并令求導后的結果等于0來求ωi

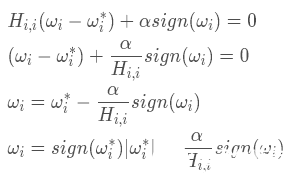
我們可以將上式中ωi 分為兩種情況，第一種是ωi 和ω?同號即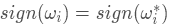，第二種是ωi 和ω?異號即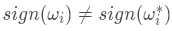，我們先討論第一種情況，為了幫助大家理解我們可以看看下圖

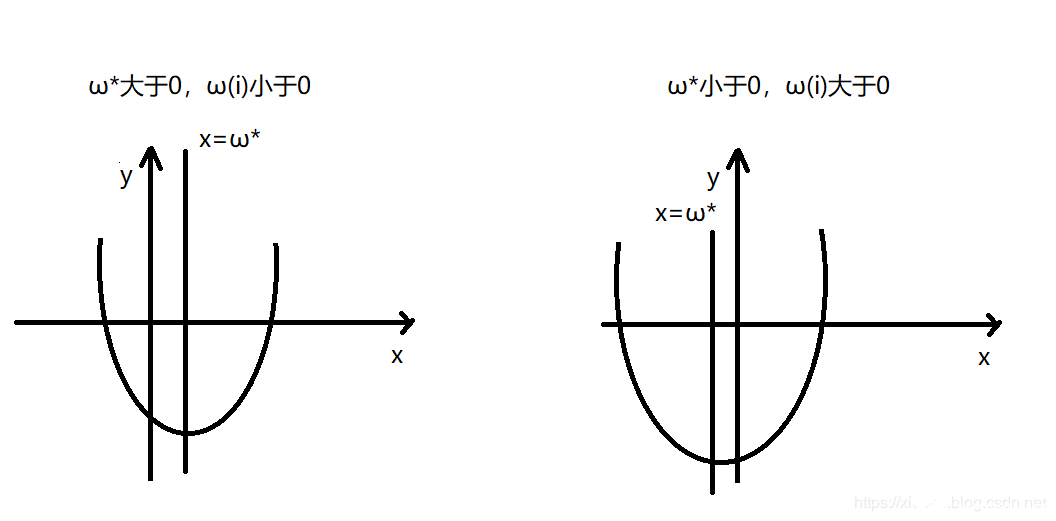
通過上圖可以發現，當ωi 與ω?異號時，無論是哪種情況為了使得損失函數最小，其最優值都是ωi=0此時能保證代價函數的二次項式和絕對值式都取得最小值。

當ωi和ω? 同號時，可以將上式進行化簡可得

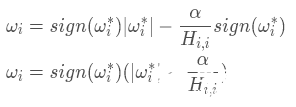
所以，我們可以合并上式的結果得到最終的ωi的表達式為

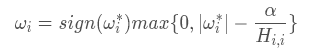
總結

我們通過畫圖和使用公式推導證明了l1正則化和l2正則化產生不同效果的原因，需要注意的是它們的共同點其實都是在衰減對于代價函數的值變化影響相對較小的權重，也就是特征值小的權重，而l1正則化的效果是會使得這部分權重為0，l2正則化會使得它們趨于0。