常用的數字濾波方法

一、平均值濾波

平均值濾波就是對多個采樣值進行平均算法，這是消除隨機誤差最常用的方法。具體又可分為如下幾種。

1. 算術平均濾波

算術平均濾波是在采樣周期T內，對測量信號y 進行m次采樣， 把m個采樣值相加后的算術平均值作為本次采樣的有效值。

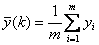
采樣次數m決定了信號的平滑度和靈敏度。提高m的值，可提高平滑度，但系統的靈敏度隨之降低，采樣次數m的取值隨被控對象的不同而不同。一般情況下，流量信號可取10左右，壓力信號可取4左右，溫度、成分等緩變信號可取2甚至不進行算術平均。

在編制算法程序時，m一般取2、4、8等2的整數冪，以便于用移位來代替除法求得平均值。

這種算法適用于存在周期性干擾的信號濾波

2.去極值平均濾波

算術平均濾波不能將明顯的偶然的脈沖干擾消除，只是把其平均到采樣結果中，從而降低了測量精度。去極值平均濾波是對連續采樣的m個數據進行比較，去掉其中的最大值與最小值，然后計算余下的m-2個數據的算術平均值。

在編制算法程序時，為便于用移位來代替除法求得平均值，m-2應取2、4、8等，故m取4、6、10等。

這種算法適用于工業場合經常遇到的尖脈沖干擾的信號濾波。

3.加權平均濾波

算術平均濾波和去極值平均濾波都存在平滑性和靈敏度的矛盾。采樣次數太少則平滑效果差，次數太多則靈敏度下降，對測量參數的變化趨勢不敏感。為協調兩者關系，可采用加權平均濾波。

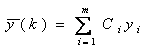
加權平均濾波是對每次采樣值乘以不同的權系數，越新的數據采樣值的權重越大。所有數據的權值之和為1。

這種算法能協調系統的平滑度和靈敏度的矛盾，提高靈敏度，更適用于純滯后較大的對象。

4.滑動平均濾波

前三種的平均濾波算法有一個共同點：即每取得一個有效采樣值必須連續進行若干次采樣。 當系統的采樣速度較慢或采樣信號變化較快時，系統的實時性就無法得到保證。滑動平均濾波是在每個采樣周期只采樣一次，將這一次采樣值和過去的若干次采樣值一起求平均，所得結果即為有效采樣值。

滑動平均濾波算法的最大優勢就是實時性好，提高了系統的響應速度。

二、中值濾波

中值濾波是將信號y?的連續m次采樣值按大小進行排序，取其中間值作為本次的有效采樣值。本算法為取中值，故采樣次數m應為奇數，一般3~5次即可。

編制中值濾波的算法程序，首先把m個采樣值從小到大（或從大到小）進行排隊，這可采用幾種常規的排序算法如冒泡算法，然后再取中間值。

中值濾波對緩變過程中的偶然因素引起的波動或采樣器不穩定造成的誤差所引起的脈動干擾比較有效，而對快速變化過程（如流量）的信號采樣則不適用。

三、限幅濾波

經驗說明，生產過程中許多物理量的變化需要一定的時間，因此相鄰兩次采樣值之間的變化幅度應在一定的限度之內。限幅濾波就是把兩次相鄰的采樣值相減，求其增量的絕對值，再與兩次采樣所允許的最大差值Y進行比較，如果小于或等于Y，表示本次采樣值y（k）是真實的，則取y（k）為有效采樣值；反之，y（k）是不真實的，則取上次采樣值y（k1）作為本次有效采樣值。

當|y（k）y（k1）|《Y時，則取y（k）=（k）

當|y（k）y（k1）|》Y時，則取y（k）=y（k-1）

式中：y（k）──t=kT時的采樣值；

y（K-1） ──t=（k-1）T時的采樣值；

Y──相鄰兩次采樣值所允許的最大偏差，其大小取決于控制系統采樣周期T和信號Y的正常變化率。

限幅濾波對隨機干擾或采樣器不穩定引起的失真有良好的濾波效果。

以上討論了幾種數字濾波方法，各有其特點。在實際應用中，究竟采用不采用、以及采用哪一種數字濾波，都應視具體情況而定。可能有的系統并不需要進行數字濾波或者應用得不恰當，非但達不到濾波效果還會降低控制品質，而有的系統采用了復合濾波方法──即把幾種濾波方法結合起來使用，可能會取得更好的濾波效果。