Grin,一種使用MimbleWimble協議的新型加密貨幣,連日來讓整個市場為之興奮。但其相關教程卻乏善可陳。
Grin輸出采用了Pedersen Commitment。輸出形式如下:
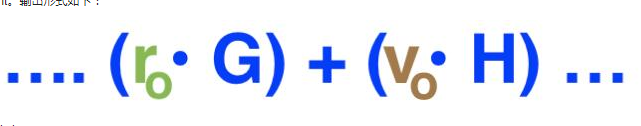
Grin輸出——Pedersen Commitment方案。
Pedersen Commitment是一種隱藏信息的巧妙方式。如果這是你第一次聽到Commitment,那么再看到這個詞語的時候你就可以將其理解為“隱藏價值”。
如果我們選擇一個非常大的數字 k 作為私鑰,則k * H被認為是相應的公鑰。即知道公鑰k * H的值,要推導出 k 的值也幾乎是不可能的。..
? r 是私鑰,用作盲因子, G 是橢圓曲線上的不動點,他們的乘積 r*G 是曲線上r的公鑰。
? v 是輸入或輸出值,H 是橢圓曲線上的另一個不動點。
在公式(k + j)* H = k * H + j * H中, k 和 j 都是私鑰,說明兩個私鑰和獲取的公鑰(k + j)* H,等于每個私鑰的對應公鑰和(k * H + j * H)。
在ECC入門中有對密碼學更深入的研究,但簡而言之,要花費Grin,就必須要知道盲因子(r)和Grin的數量(v)。而要解構commitment來推斷這些值是不可能的。我們必須提前知道這些值。
盲因子之所以存在是因為向你支付Grin的人也知道v的值是多少(他們向你發送了多少Grin)。但只有你(而非Grin的發出方)知道該輸出的盲因子,因此,只有你能夠花掉這筆輸出。
假設該筆輸出使用的盲因子為20,且該筆輸出包括40個Grin。(注:Grin的數量實際上是以原子單位1 NanoGrin的倍數發送的。簡單起見,這里我們使用“Grin”來表示。):
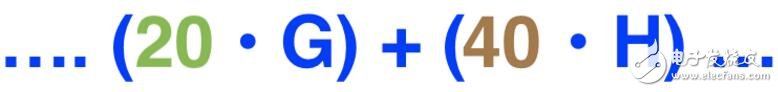
該筆輸出中,盲因子為20,Grin數量為40.
若查看Grin的區塊鏈瀏覽器,你會發現這筆輸出不會如上所述整齊地分解。以下為真正的Grin輸出,與我們所創建的一樣:

Grin輸出形式(在Commit列下)
同樣,要從該輸出中推導出“20”(盲因子)或“40”(Grin數量)是不可能的。
花費輸出
假設我們展示的輸出屬于Alice。現在,Alice希望將40個Grin中的25個發送給Bob。為方便說明,我們將忽略礦工費。
如果你用一張5美元的鈔票買了一件3美元的東西,那么你會得到2美元的找零(余額)。比特幣交易方式亦是如此,Grin也不例外。如果Alice想要從她未使用的40個Grin輸出中發送25個Grin給Bob,她也會在同樣一筆交易中創建一個輸出,這筆輸出會將余下的15個Grin(找零)返還給她自己。
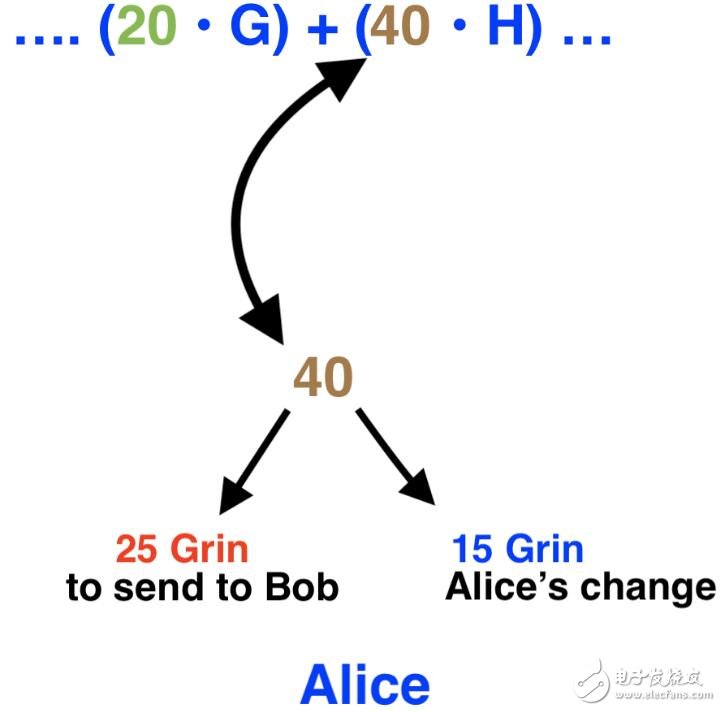
Alice確定想要發送給Bob的Grin數量,及其余額。
這15個Grin將回到Alice的賬戶中,這就意味著,只有她能夠控制并再次花費。換言之,Bob無法花費Alice的這15個找零。為此,Alice必須為這15個找零創建一個新的盲因子。假設Alice選擇34作為盲因子。
Alice既知道r值(找零輸出的盲因子),也知道v值(余下Grin數量)。這樣,她就擁有了創建找零輸出(co)所需的一切信息。這也將作為一筆輸出記錄在區塊鏈上,就像Alice很快生成的、將25個Grin發送給Bob的輸出一樣。

Alice的余額輸出。
如前所述,要花費任何一筆輸出,必須知道輸出中所使用的盲因子。Alice知道她想要花費的輸出中所使用的盲因子(20),但她需要一種方式向所有人證明她知道。
為此,她需要創建一個完全獨立的計算方法——盲因子總和。這里需要Alice用她剛剛為自己的余額輸出創建的盲因子(34),減去她希望花費的輸出的盲因子(20)。
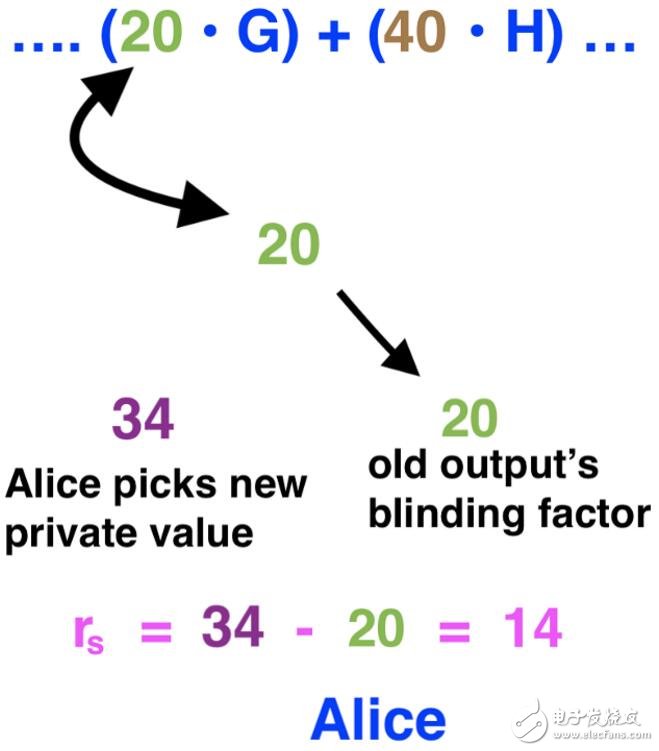
Alice的盲因子總和。
s(s代表發送方,即Alice)是Alice所有盲因子的總和,本例中總和為14。(注:本文中我有意忽略了內核偏移)。
最后,Alice要創建一個隨機數ks(s同樣代表發送方)。她將使用該隨機數為這筆交易構建簽名,我們將在稍后展示簽名的構建過程。Alice不會將實際隨機數發送給Bob。相反,她發送的是ks ? G,這是對該隨機數的承諾(commitment)。如前所述,Alice將隨機數與生成點G相乘,從而隱藏了實際隨機數的值。
Alice會將以下信息發送給Bob。但實際上,Grin數據并未被分為“元數據(Metadata)”和“數據(Data)”字段。而為了清晰起見,我們在這里會按照如下形式表示。
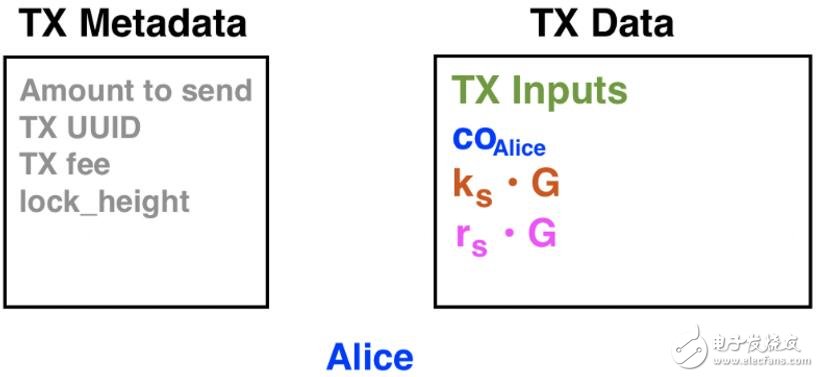
Alice在本次Grin交易的第一步中發送給Bob的所有信息。
元數據字段包括:
1. 發送數量:Alice想要發送給Bob的Grin數量(本例中為25)。
2. TX UUID:Alice和Bob在來回發送數據時用于標識此交易的唯一標識符。
3. TX fee: 交易費用(本教程中將不予討論)。
4. 區塊高度(lock_height):該筆交易生效時的區塊編號。
數據字段包括:
1. TX輸入:未花費的輸出,Alice用作與Bob進行交易的輸入。
2. co: Alice的余額輸出。
3. ks ? G: Alice的隨機數ks乘以生成點G,成為對該隨機數的承諾。
4. rs ? G: Alice所有盲因子rs的總和乘以生成點G,成為對該值的承諾。
Alice將以上全部數據發送給Bob,Bob繼續下一步操作。
輪到Bob
Bob在接收到Alice發來的數據后,將交易費用(TX fee)和區塊高度(lock_height)變量聯系起來以創建M,我們稱之為該筆交易的“信息(Message)”。

該筆交易的“信息”
Bob為他想要從Alice那里收到的25個Grin選擇一個盲因子rr(r代表接收方,在本例中為Bob)。假設他選擇11作為盲因子rr,同時還選擇了自己的隨機數kr(r同樣代表接收方)。
正如Alice所做的,Bob也分別將這兩個值乘以生成點G,創建對這兩個值的承諾。接著Bob利用這些數值,為該筆交易生成Schnorr challenge,由變量e表示:
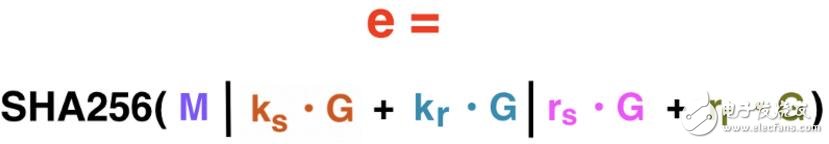
該筆交易的Schnorr challenge。
Schnorr challenge按順序包含以下內容的SHA256哈希:
1. 交易信息。
2. Alice和Bob使用隨機數的承諾總和。
3. Bob(25個Grin輸出)的盲因子承諾總和,和Alice所有的盲因子總和。
Bob使用e為交易生成他的Schnorr簽名,sr(r代表接收方)。雖然這是Bob簽名的全部內容,但我們稱之為Bob的部分簽名,因為它最終將與Alice的部分簽名相加,從而得到整個交易的簽名。
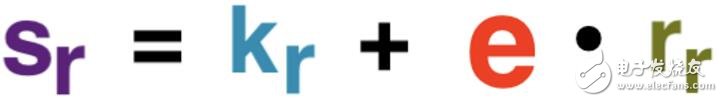
該筆交易Bob的部分簽名
當Alice最終收到sr時,她是無法從中得知kr或rr的值的。
Bob將以下內容發回給Alice:
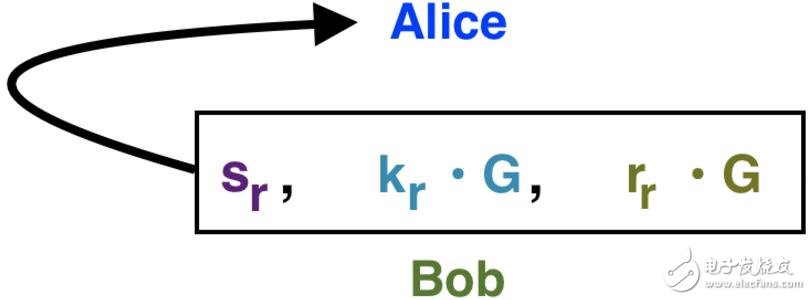
Bob將他的部分簽名、隨機數承諾以及對輸出盲因子的承諾發回給Alice。
這些內容按順序包括:
1. sr: Bob的部分簽名。
2. kr ? G: Bob的隨機數承諾
3. rr ? G: Bob對他想要得到的25個Grin的盲因子承諾
最后一步:回到Alice
Alice現在擁有所需一切信息,可以在本地計算e,即該筆交易的Schnorr challenge。在本地計算了e之后,Alice可以驗證Bob的部分簽名。
Bob的部分簽名sr包含以下內容:
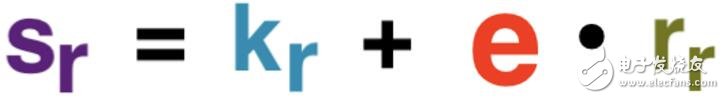
該筆交易Bob的部分簽名
基于我們前面描述的橢圓曲線的性質,Alice可將生成點G引入方程式兩邊,等式仍然成立。

Alice將等式兩邊分別乘以生成點G。
由于Alice收到了Bob的kr?G(Bob的隨機數承諾)和rr?G(Bob的盲因子承諾,他將使用該盲因子來獲得他將收到的那25個Grin),同時由于已經在本地計算了e,Alice可以簡單地乘以生成點G,并確保等式的右邊等于這個值,從而驗證Bob的部分簽名sr。
如此,Alice便證明了:
1. Bob知道他會收到多少Grin(25個)。
2. Bob知道其隨機數。
3. Bob知道他想要得到的25個Grin的盲因子。
而Alice不會知道Bob選擇的隨機數或者盲因子。
接著,Alice生成自己的部分簽名:
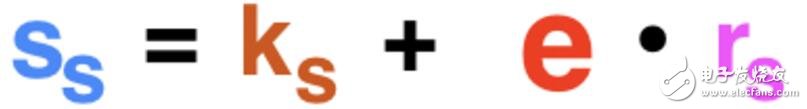
Alice為該筆交易生成部分簽名。
Alice現在可以生成交易的簽名,其中包括Alice和Bob的部分簽名:

交易簽名,包括Alice和Bob部分簽名的總和以及對其隨機數的承諾。
簽名按順序包括:
1. Alice和Bob部分簽名的總和。
2. Alice和Bob的隨機數承諾的總和(他們彼此互不知道對方的真實隨機數)。
簡化后該簽名表現為:
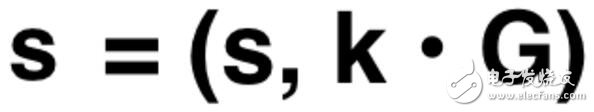
該交易的簽名
其中 s = ss + sr, k = ks + kr.
記住這個簽名,很快你就會理解它的意義。
完成交易
數字貨幣需要“記憶”——也就是說,當你將一筆錢發送給某一個人的時候,你就不能將它再發送給另一個人。而Grin的運作方式隱藏了發送的Grin數量和接收方。那么,我們怎么能證明一筆錢沒有被重復支付或憑空創造出來呢?
在一筆Grin交易中,當從輸入中減去所有輸出時,剩余Grin的數量應該等于0。那么回到之前的5美元例子:
給收銀員3美元(輸出) + 2美元找零返還給我 (輸出) – 5美元紙鈔 (輸入) = 0
在Grin的交易中,當一筆交易合法時,相同的求和使得v值總和為零。但我們如何在不展示這些數值的情況下證明這一點呢?讓我們看看從Alice到Bob的交易中使用的輸入和輸出:
(34?G) + (15?H) + (11?G) + (25?H) - (20?G) - (40?H) = (25?G) + (0?H)
這里的巧妙之處在于,當Grin的數量抵消時(不存在憑空創造的情況下應該得到的結果),從輸入減去輸出所剩下的就是“過多盲因子(the excess blinding factor)”的承諾,或“kernel excess”。本文例子中,盲因子的承諾是25?G,是曲線上的公鑰。
如果一筆Grin交易的輸出總和減去輸入總和會在曲線上產生一個有效公鑰,那么你就會知道,v值一定已經被抵消了。如果對于某個已知的n值,等式的右邊不是n?G + 0?H的形式,那么該筆交易無效。這意味著要么花費的金額大于輸入的總和(就好比你拿出5美元紙鈔,向收銀員支付3美,卻得到找零10美元),要么輸入大于輸出(就好比你拿出5美元紙鈔,向收銀員支付3美元,卻沒有找零)。
還記得這個簽名嗎?
該交易的簽名
這個簽名實際上已經對我剛剛提到的過多盲因子簽署了承諾。以下對此進行了闡釋。
如果你還記得的話,這就是當你在等式兩邊同時乘以生成點G時,Bob的部分簽名。
當兩邊同時乘以生成點G時,Bob的部分簽名。
同樣,以下為等式兩邊同時乘以生成點G后,Alice的部分簽名。
等式兩邊同時乘以生成點G后,Alice的部分簽名。
如果將兩個方程式相加會發生什么? 你會得到:
sr?G + ss?G = (kr ? G) + (ks ? G) + (e ? (rr?G + rs?G))
記住,rr是Bob的盲因子,rs是Alice的盲因子之和。前面提到的rr?G + rs?G等同于(rr + rs)?G。
Bob對其盲因子的承諾是11?G。Alice對其盲因子總和的承諾是14?G。二者相加,得到25?G,這就是對交易中過多盲因子的承諾。因此,加上sr和ss (Bob和Alice各自的部分簽名)就證明了整個交易的有效性,因為它們加起來就等于對過多盲因子的承諾。
進一步簡化該等式,我們會得到:
sr?G + ss?G = (k?G) + (e ? (r?G))
或:
sr?G + ss?G = (k?G) + (e ? (25?G))
接下來就要檢查左右兩邊是否相等。
記住,這個等式中的所有內容(部分簽名的總和,e中的所有內容,對過多盲因子的承諾,對隨機數總和的承諾)都是公開可見的,因此任何人都可以對此進行驗證。我們既不需要Alice也不需要Bob的盲因子來驗證交易。加上他們的部分簽名,并驗證他們對過多盲因子的承諾進行了求和,我們就證明了:
1. 在花費Alice之前的輸入時,沒有憑空創造新的資金。
2. Alice和Bob在創建該筆交易時都知道其輸出的盲因子。這意味著他們可以花費新的輸出,不會出現問題。
我們用來驗證交易的信息被放在交易內核中。
交易內核
除輸出外,交易內核是從Grin交易輸出中得到的另一條信息。每筆交易都會生成一個交易內核,但是Grin區塊鏈是無法查看的,也無法將一筆輸出與交易內核相關聯。每筆Grin交易都存在一個交易內核,其中包含了“沒有憑空創造新的資金”的證明。
交易內核中存儲信息如下:
1. 交易的簽名(s, k ? G)。
2. 與“過多盲因子”相關的公鑰(在本例中為25?G)。如上所述,可用其驗證s。
3. 交易費和交易的區塊高度。(注:如果是Coinbase交易,則這兩者均不存在)。
總結
完成以上操作后,從該筆交易向網絡中廣播的信息僅包括:
1. 使用的輸入。
2. 新的輸出。
3. 交易內核。
4. 內核偏移。
 電子發燒友App
電子發燒友App



















評論