我們相信基于代理的仿真可以幫助分析智能合約和協議行為。但也存在其他方法，比如形式驗證。形式驗證使邏輯保證比模擬的統計保證更強。在回答我們關心的安全問題方面，它是否優于激勵模擬？在這篇文章中，我們探討了形式化驗證，并認為它是對模擬的有力補充。

概述

形式驗證可以提供對智能合約邏輯和安全性的獨特見解。然而，當試圖對一份智能合約的財務結果進行陳述時，形式是不夠的。

基于代理的模擬允許一組模擬代理與合約交互。們的目標是應用形式驗證技術來自動發現Uniswap交換上的有效合約操作，并分析一系列交易。

使用代理的目的有兩方面：它允許我們預測協議設計階段的實際使用，并支持在實現階段進行驗證。代理模擬允許我們預測真實用戶與合約交互時的行為。

后續的博客文章將展示如何在激勵模擬中使用更有效的隨機技術來獲得關于Uniswap的一些見解。

第1部分。Uniswap合約的高級概覽

Uniswap exchange是一組智能合約，允許任何人在不向訂單簿提交訂單的情況下交易以太幣和ERC20代幣。單個Uniswap交換合約支持特定的以太幣/ERC20代幣，任何人都可以使用Uniswap合約創建新的代幣對。一旦交易所成立，它就會自主運作：

· 流動性的創造。流動資金提供者將首先按當前匯率提供以太幣和代幣。可以在任何時候添加/刪除更多。

· 交易。然后，市場參與者可以直接使用Uniswap交易所合同進行交易。

· 定價算法。給定交易的價格是使用“常數產品做市商”模型自動確定的。在給定的貿易期間，Uniswap將設置價格，以便保存產品（x * y = k）的以太幣量和給定的代幣。

· 流動性的費用。小額費用被征收并分配給流動性提供者。

第2部分。如何測試區塊鏈系統的安全性

要想知道Uniswap這樣的系統是否安全，我們需要回答兩個問題：

· 正確性。代碼是否遵循我們預期的模型（作為規范或其他形式編寫）？

· 有效性。我們想要的模型會激勵我們想要的行為嗎？

形式驗證只對前者有一些幫助，而對后者幾乎沒有幫助。像“我們應該如何設置費率”這樣的問題根本無法通過形式驗證來回答。

第3部分。Uniswap智能合約的形式驗證歷史

形式驗證

許多項目都嘗試使用形式驗證技術來證明他們的合約是正確的。對于相對簡單的智能合約，這是非常可行的。形式驗證和程序分析技術可以確定代碼是否遵循給定的規范，而且常常會出現致命的反例。

之前的工作

Uniswap現有的輕量級形式驗證就是使用這些技術可以實現的一個很好的例子。利用KEVM框架驗證了做市商（x * y = k）模型及其通過addLiquidity、removeliquity、ethToTokenSwapInput和ethToTokenSwapOutput的實現。假設現有的ERC20合約“表現良好”。

在共識系統調查公司（consensus sys Diligence）的后續審計中，該團隊能夠推斷出如果打破這一假設會發生什么。他們發現，ERC20代幣的惡意實現可以用來欺騙市場參與者，讓攻擊者重新進入Uniswap合約，以同樣的成本消耗更多的資金。

原則上，可以將此擴展規范捕獲為代碼模板。可以表示和調用一個半ERC20兼容的合約（相同的接口，但不一定是ERC20行為），并嘗試使用形式驗證來發現攻擊。在實踐中，這使得形式驗證問題在計算上更加復雜，因為當用于發現任意程序時，底層SMT解決程序中的分支會增加。這種技術有時被稱為“程序綜合”。微軟研究院的這項調查是了解更多信息的良好起點。

這些挑戰說明了與形式驗證（包括程序綜合）相關的另外兩個限制：

· 完整的規范在編寫和表達方面可能具有挑戰性。

· 目前的形式驗證器只適用于簡單的合約和簡單的規范。

第4部分。我們如何應用形式驗證

制定問題

為了測試合約在一組代理的影響下的行為，我們首先嘗試使用符號分析將其應用于自動化操作發現。符號分析將代碼轉換成一組可以由SMT求解器求解的公式。SMT求解器是SAT求解器的擴展，它超越了布爾公式（對簡單命題進行陳述）到包含inte的公式

符號分析將代碼轉換成一組可以由SMT求解器求解的公式。SMT求解器是SAT求解器的擴展，它超越了布爾公式（對簡單命題進行陳述），涉及整數、位向量、數組和編程中常見的其他數據形式的公式。

一種看待符號分析的簡單方法是，它可以被用來正式指定一個關于給定的智能合約的假設，證明假設為真，或者生成一個反例。

例如，在形式驗證中，假設通常是關于合約的斷言，例如，“double函數返回的值總是偶數”。

pragma solidity ^0.5.1

contract Doubler {

function double（uint x） pure public returns （uint） {

uint y = 2 * x;

require （y % 2 == 0）; // This assertion could be checked via FV

return y;

}

}

我們正在尋找在某些交易集中給定斷言是否為true的驗證。

為了使用符號分析進行操作發現，我們設置了以下假設：“Uniswap合約不支持有效的交易”。如果這被證明是錯誤的，那么反例將是生成有效合約交易的一組輸入。

具有象征意義的分析

我們提供了一個黑盒符號解釋器，其中包含一個經過修改的Uniswap交換合約、一個可用資金支持的一條縫帳戶代理池和一組受限制的操作（與合約功能匹配）。在兩個測試鏈上重播完成的操作——一致測試鏈和一個純EVM副本（為了保存對契約存儲的更改而進行維護）。目標是發現一組有效的參數來完成交易并推進當前狀態。

第5部分。我們的結果以及為什么我們不認為形式正式的驗證是測試安全性的完整解決方案

這種方法是站住腳的，但是我們發現了這個特殊合同的三個限制，這表明了符號分析和一般形式驗證的挑戰：

1. 表現不佳

2. 應用優化來選擇操作的難度

3. 修改合同/設置的必要性，在這種情況下是為了執行：內聯調用、刪除截止日期考慮事項和發送操作

我們相信挑戰1-2可以通過使用隨機模擬來克服，因此我們得出結論，符號分析最好用于戰術上驗證合約/模型的某些方面，或者支持其理解。下面我們詳細介紹我們的方法并解釋我們的發現。

1. 表現不佳

我們使用一個基于重寫的有界模型檢查器來進行符號分析，它在EVM字節碼級別上運行。它與Mythril和Manticore等基于狀態的符號解釋器的不同之處在于，它在合約塊完全擴展之后一次性應用SMT-solver，而不是在發現每個塊時增量地應用。另一個區別是，假陰性是不能容忍的。我們使用的底層SMT解決程序是Z3。解釋器包含幾個優化，我們將在下面詳細介紹。

作為輸出，我們提取了參數數組（也稱為CALLDATA）并使用合約接口，將其轉換為相關合約函數的一組有效的高級參數。

我們從字節碼合約直開始，并實現了幾個優化：

· 一個多級反編譯器與塊修剪

· Z3上的自定義包裝器，帶有用于非決定論的操作符

· 公共數據的模塊化表示

· EVM級別的二進制類型

· 先進的具體化

這是每個功能/動作的性能：

［所有時間在2013年MacBook Air上測量，i7 8GB］

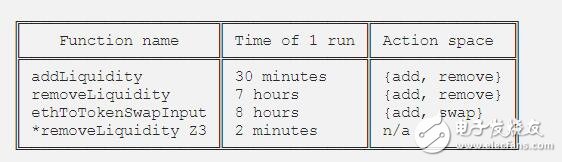
最后一個加星的例子是直接實現Z3的流動性函數，例如，一個代表性的“理論最小值”。操作空間表示哪些合約函數可用作代理的操作。Add代表addLiquidity，等等。

為了解釋這些結果，我們必須解釋符號分析器的性能特征。在我們的示例中，超過90%的計算時間直接花費在SMT求解程序中。因此，性能優化的大部分工作都花在優化如何重寫SMT求解程序的合約上。

不幸的是，位向量乘法對目前的SMT求解器是一個挑戰。讓我們假設SMT求解器的性能（非常）松散地與所需的命題項數量相關。為了說明這一點，EVM中的每個數字都表示為一個256位的單詞。在Z3中，這些單詞進一步“分解”為表示每個位的256個命題變量。表示位向量乘法需要多達256個部分和，每個部分和表示另一個256位單詞，需要65，000個變量。移除性函數包含四個乘法

這些單詞被進一步“分解”為表示每個位的256個命題變量。表示位向量乘法需要多達256個部分和，每個部分和表示另一個256位單詞，需要65，000個變量。流動性函數總共包含四次乘法。

雖然SMT求解器的性能無法以任何直接或算術的方式預測，但是乘法和除法對該契約的影響也通過從源中刪除它得到了獨立的驗證（產生的運行時可以忽略不計）。

這是一個很好的例子，在這個例子中，概念簡單的合約可能需要不可預測的大量解決方案時間。一般來說，非專業人員很難預測SMT-solver的性能，正如我們所看到的，它并不一定與所使用的代碼行或其他容易識別的指標相關。

2. 應用優化來選擇操作的難度

使SMT解決方案對這個應用程序具有吸引力的是它發現最優操作的潛力。優化SMT求解器“vZ”作為Z3的一部分，支持根據優化的變量求解有效的最優反例。它結合了各種子問題的優化算法。

優化vZ的求解器接口--Bj?rner等人的優化SMT求解器。

我們完成了實驗，以確定優化求解器是否可以用來發現最優的交易，根據給定的價格時間表，但不幸的是，求解器運行會超過24小時。

我們認為優化在特定的情況下仍然是計算上可行的，比如合約更簡單，優化問題很容易映射到“vZ”中可用的算法，例如線性問題的單純形法。

3.修改合約的必要性

在形式驗證中，降低合約復雜度（特別是在字節碼級別）對于性能至關重要，或者是應用依賴于輸入結構的形式化驗證器的先決條件。

我們對Uniswap合約所做的關鍵修改是去掉與子調用和外部調用相關的復雜性，并將重點放在交換邏輯上：

·刪除內部和外部子調用，內聯內部調用，并在合同內部建模ERC20帳戶持有

·刪除發送行為

·刪除時間戳的截止日期約束

符號分析在激勵仿真中的作用

在這篇博客文章中，我們展示了與基于代理的模擬相比，符號分析在分析像Uniswap這樣的復雜系統時是多么的不足。也就是說，形式驗證是一個重要和有力的工具。但它在戰術上最好是作為更廣泛的激勵模擬的補充：

·模型驗證。驗證一個簡化的仿真模型

·提取模型。通過驗證操作，幫助從代碼中自動提取模型

·官方的建議。為仿真提供新的或極端的啟動狀態

·局部優化。使用內置的優化器驗證關于局部最優性的假設