分組碼,分組碼 是什么意思
分組碼,分組碼 是什么意思
分組碼是一組固定長度的碼組,可表示為(n , k),通常它用于前向糾錯。在分組碼中,監(jiān)督位被加到信息位之后,形成新的碼。在編碼時,k個信息位被編為n位碼組長度,而n-k個監(jiān)督位的作用就是實現(xiàn)檢錯與糾錯。當分組碼的信息碼元與監(jiān)督碼元之間的關系為線性關系時,這種分組碼就稱為線性分組碼。
對于長度為n的二進制線性分組碼,它有![]() 種可能的碼組
種可能的碼組![]() ,從種碼組中,可以選擇M=
,從種碼組中,可以選擇M= ![]() 個碼組(k
個碼組(k
線性分組碼是建立在代數(shù)群論基礎之上的,各許用碼的集合構(gòu)成了代數(shù)學中的群,它們的主要性質(zhì)如下:
(1)任意兩許用碼之和(對于二進制碼這個和的含義是模二和)仍為一許用碼,也就是說,線性分組碼具有封閉性;
(2)碼組間的最小碼距等于非零碼的最小碼重。
在8.2.1節(jié)中介紹的奇偶監(jiān)督碼,就是一種最簡單的線性分組碼,由于只有一位監(jiān)督位通常可以表示為(n,n-1),式(1)表示采用偶校驗時的監(jiān)督關系。在接收端解碼時,實際上就是在計算:
![]() (2)
(2)
其中,![]()
![]() …
…![]() 表示接收到的信息位,
表示接收到的信息位,![]() 表示接收到的監(jiān)督位,若S=0,就認為無錯;若S=1就認為有錯。式(2)被稱為監(jiān)督關系式,S是校正子。由于校正子S的取值只有“0”和“1”兩種狀態(tài),因此,它只能表示有錯和無錯這兩種信息,而不能指出錯碼的位置。
表示接收到的監(jiān)督位,若S=0,就認為無錯;若S=1就認為有錯。式(2)被稱為監(jiān)督關系式,S是校正子。由于校正子S的取值只有“0”和“1”兩種狀態(tài),因此,它只能表示有錯和無錯這兩種信息,而不能指出錯碼的位置。
設想如果監(jiān)督位增加一位,即變成兩位,則能增加一個類似于式(2)的監(jiān)督關系式,計算出兩個校正子![]() 和
和![]() ,
,![]()
![]() 而共有4種組合:00,01,10,11,可以表示4種不同的信息。除了用00表示無錯以外,其余3種狀態(tài)就可用于指示3種不同的誤碼圖樣。
而共有4種組合:00,01,10,11,可以表示4種不同的信息。除了用00表示無錯以外,其余3種狀態(tài)就可用于指示3種不同的誤碼圖樣。
同理,由r個監(jiān)督方程式計算得到的校正子有r位,可以用來指示![]() -1種誤碼圖樣。對于一位誤碼來說,就可以指示
-1種誤碼圖樣。對于一位誤碼來說,就可以指示 ![]() -1個誤碼位置。對于碼組長度為n、信息碼元為k位、監(jiān)督碼元為r=n - k位的分組碼(常記作(n,k)碼),如果希望用r個監(jiān)督位構(gòu)造出r個監(jiān)督關系式來指示一位錯碼的n種可能,則要求:
-1個誤碼位置。對于碼組長度為n、信息碼元為k位、監(jiān)督碼元為r=n - k位的分組碼(常記作(n,k)碼),如果希望用r個監(jiān)督位構(gòu)造出r個監(jiān)督關系式來指示一位錯碼的n種可能,則要求:
![]() (3)
(3)
下面通過一個例子來說明線性分組碼是如何構(gòu)造的。設分組碼(n , k)中k = 4,為了能夠糾正一位錯誤,由式(3)可以看到,要求r ≥ 3,若取r = 3,則n = k+r = 7。因此,可以用![]() 表示這7個碼元,用
表示這7個碼元,用![]() 、
、![]() 、
、![]() 表示利用三個監(jiān)督方程,通過計算得到的校正子,并且假設
表示利用三個監(jiān)督方程,通過計算得到的校正子,并且假設![]() 、
、![]() 、
、 ![]() 三位校正字碼組與誤碼位置的關系如表1(當然,也可以規(guī)定成另一種對應關系,這并不影響討論的一般性):
三位校正字碼組與誤碼位置的關系如表1(當然,也可以規(guī)定成另一種對應關系,這并不影響討論的一般性):
由表中規(guī)定可已看到,僅當一錯碼位置在![]() 時,校正子
時,校正子![]() 為1;否則
為1;否則![]() 為0。這就意味著
為0。這就意味著 ![]() 四個碼元構(gòu)成偶數(shù)監(jiān)督關系:
四個碼元構(gòu)成偶數(shù)監(jiān)督關系:
![]() (4a)
(4a)
同理,![]() 構(gòu)成偶數(shù)監(jiān)督關系:
構(gòu)成偶數(shù)監(jiān)督關系:
![]() (4b)
(4b)
表1校正字與誤碼位置

以及![]() 構(gòu)成有數(shù)監(jiān)督關系:
構(gòu)成有數(shù)監(jiān)督關系:
![]() (4c)
(4c)
在發(fā)送端編碼時![]() 是信息碼元,它們的值取決于輸入信號,因此是隨機的。
是信息碼元,它們的值取決于輸入信號,因此是隨機的。![]() 是監(jiān)督碼元,它們的取值由監(jiān)督關系來確定,即監(jiān)督位應使式(4)的三個表達式中的
是監(jiān)督碼元,它們的取值由監(jiān)督關系來確定,即監(jiān)督位應使式(4)的三個表達式中的![]() 、
、 ![]() 和
和![]() 的值為零(表示編成的碼組中應無錯碼),這樣式(4)的三個表達式可以表示成下面的方程組形式:
的值為零(表示編成的碼組中應無錯碼),這樣式(4)的三個表達式可以表示成下面的方程組形式:
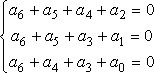 (5)
(5)
由上式經(jīng)移項運算,接出監(jiān)督位
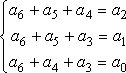 (6)
(6)
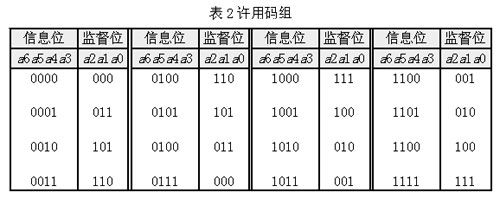
根據(jù)上面兩個線性關系,可以得到16個許用碼組如表2所示:
表2許用碼組
接收端收到每個碼組后,計算出![]() 、
、![]() 和
和![]() ,如不全為0,則可按表8-4確定誤碼的位置,然后予以糾正。例如,接收碼組為0000011,可算出
,如不全為0,則可按表8-4確定誤碼的位置,然后予以糾正。例如,接收碼組為0000011,可算出![]()
![]()
![]() =011,由表8-4可知在
=011,由表8-4可知在 ![]() 位置上有一誤碼。
位置上有一誤碼。
不難看出,上述(7,4)碼的最小碼距![]() ,因此,它能糾正一個誤碼或檢測兩個誤碼。如超出糾錯能力,則反而會因“亂糾”而增加新的誤碼。
,因此,它能糾正一個誤碼或檢測兩個誤碼。如超出糾錯能力,則反而會因“亂糾”而增加新的誤碼。
監(jiān)督矩陣H和生成矩陣G
式(5)所述(7,4)碼的三個監(jiān)督方程式可以重新改寫為如下形式:
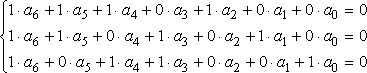 (7)
(7)
對于式(7)可以用矩陣形式來表示:
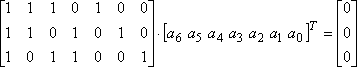 (8)
(8)
上式可以記作:![]() 或
或 ![]() ,其中
,其中
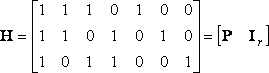 (9a)
(9a)
![]() (9b)
(9b)
![]() (9c)
(9c)
通常H稱為監(jiān)督矩陣,A稱為信道編碼得到的碼字。在這個例子中H為r×n階矩陣,P為r×k階矩陣,Ir為r×r階單位矩陣,具有這種特性的H矩陣稱為典型監(jiān)督矩陣,這是一種較為簡單的信道編譯碼方式。典型形式的監(jiān)督矩陣各行是線性無關的,非典型形式的監(jiān)督矩陣可以經(jīng)過行或列的運算化為典型形式。
對于式(6)也可以用矩陣形式來表示:
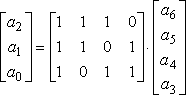
或者
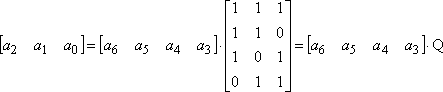 (10)
(10)
比較式(9a)和式(10)可以看到 ![]() ,如果在Q矩陣的左邊在加上一個k×k的單位矩陣,就形成了一個新矩陣G:
,如果在Q矩陣的左邊在加上一個k×k的單位矩陣,就形成了一個新矩陣G:
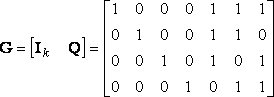 (11)
(11)
這里G稱為生成矩陣,利用它可以產(chǎn)生整個碼組
![]() (12)
(12)
由式(11)表示的生成矩陣形式稱為典型生成矩陣,利用式(12)產(chǎn)生的分組碼必為系統(tǒng)碼,也就是信息碼元保持不變,監(jiān)督碼元附加在其后。
校驗子S
在發(fā)送端信息碼元M利用式(12),實現(xiàn)信道編碼,產(chǎn)生線性分組碼A;在傳輸過程中有可能出現(xiàn)誤碼,設接收到的碼組為B。則收發(fā)碼組之差為:
![]() (13)
(13)
這里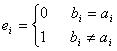 ,
,![]() ,表示i位有錯,
,表示i位有錯,![]() ,表示i位無錯。基于這樣的原則接收端利用接收到的碼組B計算校正子:
,表示i位無錯。基于這樣的原則接收端利用接收到的碼組B計算校正子:
![]() (14)
(14)
因此,校正子僅與E有關,即錯誤圖樣與校正子之間有確定的關系。
對于上述(7,4)碼,校正子S與錯誤圖樣的對應關系可由式(14)求得,其計算結(jié)果見表3所示。在接收端的譯碼器中有專門的校正子計算電路,從而實現(xiàn)檢錯和糾錯。
表3(7,4)碼校正子與錯誤圖樣的對應關系
?
非常好我支持^.^
(29) 100%
不好我反對
(0) 0%
相關閱讀:
- [電子說] 采用VHDL語言實現(xiàn)線性分組碼編/譯碼器的設計與仿真驗證 2019-05-03
- [電子常識] 分組碼和卷積碼的區(qū)別 詳解分組碼和卷積碼 2018-08-21
- [衛(wèi)星通信] 線性分組碼,線性分組碼是什么意思 2010-04-03
( 發(fā)表人:admin )
