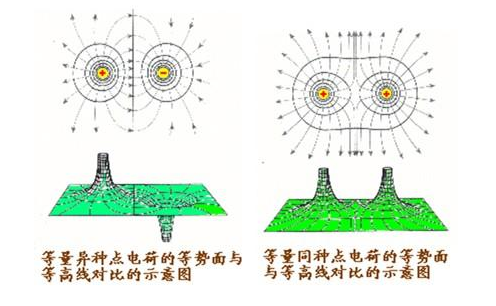
在靜電學里,電勢能(Electric potential energy)是處于電場的電荷分布所具有的勢能,與電荷分布在系統(tǒng)內部的組態(tài)有關。電勢能的單位是焦耳。電勢能與電勢不同。電勢定義為處于電場的電荷所具有的電勢能每單位電荷。電勢的單位是伏特。
電勢能的計算公式
電勢能:EA=qφA {EA:帶電體在A點的電勢能(J),q:電量(C),φA:A點的電勢(V)}
E=kq1q2/r^2
庫侖力的公式是F=kQq/r^2
那么在庫侖力的作用下,當電荷移動一個微小的距離dr時所做的微功dW=Fdr
假設現(xiàn)在電荷Q固定,那么當q從與Q的距離為R1的地方運動到R2的地方(R1《R2)時,根據(jù)定積分W=∫dW=∫Fdr=∫(kQq/r^2)dr=kQq∫(dr/r^2)= -kQq∫d(1/r)
積分區(qū)間為R1到R2
因此有W=-kQq(1/R2 - 1/R1) = kQq/R1 - kQq/R2
如果Q和q同號,顯然,電場力做正功,你可以去分析
而 kQq/R1 和 kQq/R2 這兩個參數(shù)反應的就是電荷q在Q的電場內所具有的電勢能,反過來也可以說是Q在q的電場內具有的電勢能。
電勢能變化量
(1)電場力做的功與電勢能變化量
起點和終點狀態(tài)靜止的點電荷,電場力做功與電勢能變化量的關系:
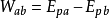
電勢能的變化量也可以表示為△Ep=Epb-Epa,因此有Wab=-△Ep 。
(2)動能變化量與電勢能變化量
根據(jù)能量守恒定律還可以得到,一般情況下,無外力做功的運動電荷,動能變化量與電勢能變化量的關系:
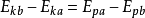
如果是外力使電勢能增加,那么其他形式的能轉化為電勢能,外力做正功,電場力做負功,電勢能增加;
如果是電場力使物體運動,那么電勢能轉化為動能,電場力做正功,物體動能增加,電勢能減小;
如果是物體運動使電勢能增加,那么動能轉化為電勢能,物體動能減少,電場力做負功,電勢能增加。
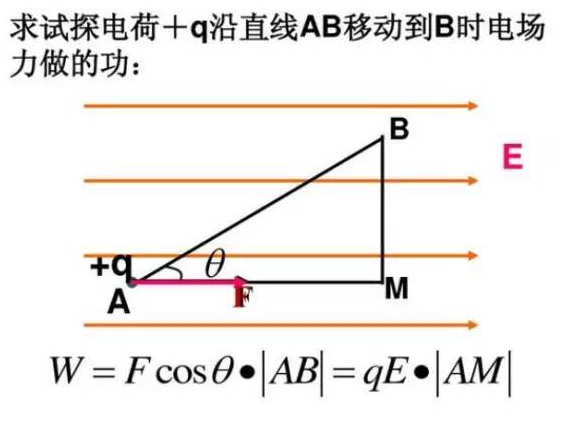
靜電場中的勢能。一點電荷在靜電場中某兩點(如A點和B點)的電勢能之差等于它從A點移動到另B點時,靜電力所作的功。 故WAB=qEd (E為該點的電場強度,d為沿電場線的距離) ,電勢能是電荷和電場所共有的,具有統(tǒng)一性。
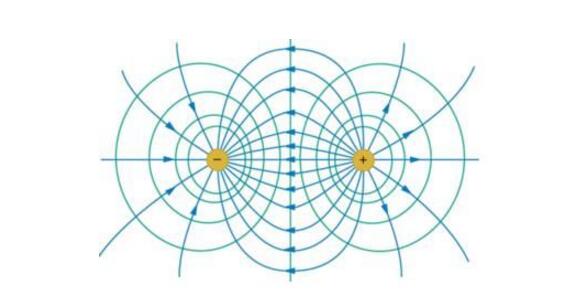
電勢能反映電場和處于其中的電荷共同具有的能量。
電勢能可以由電場力做功求得,因為 WAB=qUAB=q(ΦA-ΦB)=qΦA-qΦB=EA(初)-EB(末)= -△E,
(Φ為電勢,q為電荷量,U為電勢差,EA(初)、EB(末)為兩個點的電勢能)。
電場力做功跟電勢能變化關系:
WAB》0,△Ep《0,電場力做正功,電勢能減小~轉化成其他形式的能;
WAB《0,△Ep》0,電場力做負功,電勢能增加~其它形式的能轉化成電勢能。
順著電場線,A→B移動,若為正電荷,則WAB》0,則UAB=ΦA-ΦB》0,則Φ↓,則正Ep↓;
若為負電荷,則WAB《0,則UAB=ΦA-ΦB》0,則Φ↓,則負Ep↑。
逆著電場線,B→A移動,若為正電荷,則WBA《0,則UBA=ΦB-ΦA《0,則Φ↑,則正Ep↑;
若為負電荷,則WBA》0,則UBA=ΦB-ΦA《0,則Φ↑,則負Ep↓;
靜電力做的功等于電勢能的減少量。
做功判斷法:無論正負電荷,電場力做正功,電荷的電勢能就一定減小,電場力做負功,電荷的電勢能就一定增加
零勢能處可任意選擇,但在理論研究中,常取無限遠處或大地的電勢能為0.
取無窮遠為電勢零:
①正電荷產生的電場中Φ》0,遠離場源電荷Φ↓:移動正檢驗電荷W》0,Ep↓;
移動負檢驗電荷W《0,Ep↑。
②。負電荷產生的電場中Φ《0,遠離場源電荷Φ↑:移動正檢驗電荷W《0,Ep↑;
移動負檢驗電荷W》0,Ep↓。
 電子發(fā)燒友App
電子發(fā)燒友App




























評論