基本門電路及其組合
???門電路是實現各種邏輯關系的基本電路,是組成數字電路的最基本單元。從邏輯功能上看,有與門、或門和非門,還有由它們復合而成的與非門、或非門、與或非門、異或門等。從生產工藝上看,門電路又可分為兩大類:分立元件門電路和應用集成電路工藝制成的集成門電路。在學習這些邏輯電路時,不必考慮它的內部結構原理,而要著重掌握它們的邏輯功能。
??? 1.狀態的表示
??? 邏輯是指事物的因果關系所遵循的規律。世間萬物大多存在著對立統一的正反兩種邏輯狀態,如事物的真或假、電位(也叫電平)的高或低、開關的通或斷等。若將其中一種狀態規定為邏輯“真”,則另一種狀態便為邏輯“假”。通常將邏輯量在形式上數字化,即用1表示邏輯“真”,用0表示邏輯“假”。這時的0和1不再有數的意義,而是兩個符號,表示兩種對立的邏輯狀態。數字電路中,電路的工作狀態最終體現于電平的高或低,什么樣的電信號是高電平或低電平呢?這取決于電路元件參數和電源電壓的大小。在廣泛使用的TTL集成電路和計算機系統中,電源電壓采用5 V,它的標準高電平值是2.4 V,標準低電平值是0.4 V,只要實際的電平值≥2.4 V,即認為是高電平,實際的電平值≤0.4 V,即認為是低電平。
若規定高電平為1,低電平為0,稱為正邏輯系統。若規定低電平為1,高電平為0,則稱為負邏輯系統。本書中采用的都是正邏輯系統。
??? 2.基本邏輯門電路
??? (1).與門
??? 在邏輯問題中,如果決定某一事件發生的多個條件必須同時具備事件才能發生,則稱這種因果關系為與邏輯。例如,在圖8-1所示電路中,開關A和B串聯控制燈Y。顯然,僅當兩個開關均閉合時(條件),燈才能亮(結果)。否則,燈滅。實現與邏輯關系的電路稱為與門電路,如圖8-2所示的是最簡單的二極管與門電路。A、B是它的兩個輸入端,Y是輸出端。也可以認為A、B是它的兩個輸入變量,Y是輸出變量。假設輸入信號低電平為0 V,高電平為3 V,按輸入信號的不同可有下述幾種情況(忽略二極管正向壓降)。
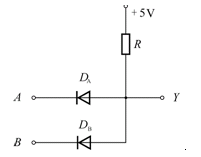
???? ① 輸入端全為高電平,DA、DB均導通,則輸出VY=3V。
???? ② 輸入端有一個或兩個為低電平。例如VA=0V, VB=3V時, DA先導通,這時 承受反向電壓而截止,輸出VY=0V。
??? 可見,只有當輸入端A、B全為高電平1時,才輸出高電平1,否則輸出端均為低電平0,這合乎與門的要求。
??? 將邏輯電路所有可能的輸入變量和輸出變量間的邏輯關系列成表格,如表8-1所示,稱為真值表。
?????????????????????????????????????????????????????????? 表8-1 與門真值表
|
A |
B |
Y |
|
0 |
0 |
0 |
|
0 |
1 |
0 |
|
1 |
0 |
0 |
|
1 |
1 |
1 |
??? 上述邏輯關系可用邏輯表達式描述為:
???????????????????????????????????? Y=A?B?????????????????????????????? (8-1)
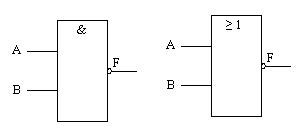
??? 式中小圓點“?”表示A、B的與運算,也表示邏輯乘。在不致引起混淆的前提下,“?”常被省略。在某些文獻中,也有用符號∧表示與運算的。圖8-3所示為兩輸入端的與門邏輯符號。與門也可有兩個以上的輸入端。
式中小圓點“?”表示A、B的與運算,也表示邏輯乘。在不致引起混淆的前提下,“?”常被省略。在某些文獻中,也有用符號∧表示與運算的。圖8-3所示為兩輸入端的與門邏輯符號。與門也可有兩個以上的輸入端。
?? 門電路的邏輯關系也可以用波形圖來描述,如圖8-4所示。
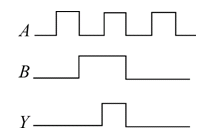
?? 2.或門
???? 在邏輯問題的描述中,如果決定某一事件發生的多個條件中,只要有一個或一個以上條件成立,事件便可發生,則稱這種因果關系為或邏輯。例如,在圖8-5所示電路中,開關A和B并聯控制燈Y。可以看出,當開關A、B中有一個閉合或者兩個均閉合時,燈Y即亮。因此,燈Y與開關A、B之間的關系是或邏輯關系。
??? 實現或邏輯關系的電路稱為或門電路。圖8-6所示是最簡單的二極管或門電路。A、B是它的兩個輸入,Y是輸出。采用與門電路同樣的分析方法,對不同的輸入組合,不難得出或門電路的真值表,如表8-2所示。
??????????????????????????????????????????????????????? 表8-2 或門真值表
|
A |
B |
Y |
|
0 |
0 |
0 |
|
0 |
1 |
1 |
|
1 |
0 |
1 |
|
1 |
1 |
1 |
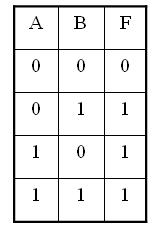
??? 從表中可知,輸入變量只要有一個為1時,輸出就為1;只有輸入全為0,輸出才為0。
?? 上述邏輯關系用邏輯表達式描述為:
?????????????????????????????????????? Y=A+B?????????????????????????? (8-2)
??? 式中,“+”號表示邏輯或而不是算術運算中的加號。某些文獻中也用“∨”表示或運算。圖8-7為兩輸入端的或門邏輯符號。或門也可有兩個以上的輸入端。
或門電路的邏輯關系也可用波形圖來描述,如圖8-8所示。
??? (3).非門
??? 在邏輯問題中,如果某一事件的發生取決于條件的否定,即事件與事件發生的條件之間構成矛盾,則這種因果關系稱為非邏輯。
??? 例如,在圖8-9所示電路中,當開關A斷開時,燈亮;A閉合時,燈不亮。這個例子表示了一種條件與結果相反的非邏輯關系。
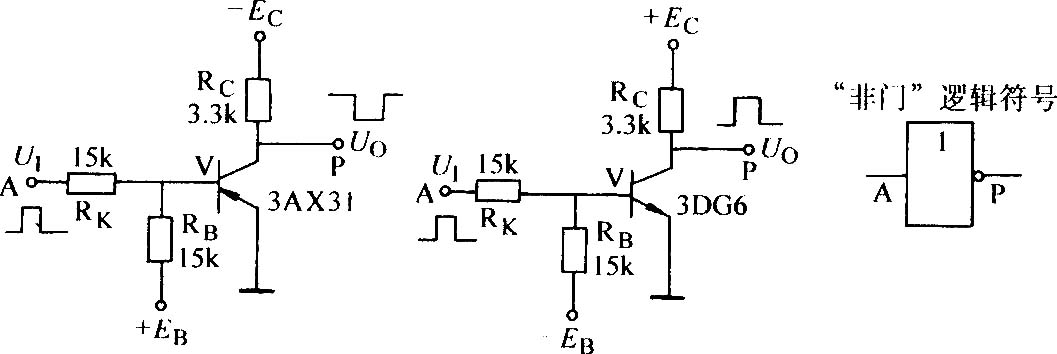
?? 圖8-10所示為三極管非門電路。非門又稱反相器,它只有一個輸入端和一個輸出端,其輸出與輸入恒為相反狀態。
?? 下面分析該三極管(工作在飽和或截止狀態)非門電路的邏輯功能。
?? ① 當輸入端A為高電平(VA=3V)時,適當選取RK、RB之值可使三極管飽和導通,其集電極輸出低電平(VY=0V)。
?? ② 當輸入端A為低電平(VA=0V)時,負電源UBB經RK、RB分壓使三極管基極電位為負,三極管截止,從而輸出高電平(其電位近似等于UCC)。
?? 表8-3是非門電路的邏輯真值表,非門的邏輯符號如圖8-11所示。
?????????????????????????????????????????????????????????? 表8-3 非門真值表
|
A |
Y |
|
0 |
1 |
|
1 |
0 |
?? 如果用邏輯表達式描述,則為:
??????????????????????????????? 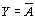 ?????????????????????????? (8-3)
?????????????????????????? (8-3)
?? 它可和圖8-12的波形圖相對照。
3.基本邏輯門電路的組合
?? 利用與門、或門、非門三種最基本的門電路可以組成各種復合門電路,其中最常用的有與非門電路、或非門電路、異或門電路等。
?? (1).與非門
?? 與非門電路是數字電路中運用最廣的一種邏輯門電路,邏輯符號及波形圖如圖8-13所示。
????與非門的邏輯功能為:輸入信號全為1,則輸出為0;只要有一個輸入為0,則輸出為1。與非門真值表如表8-4所示。
????????????????????????????????????????????????????????? 表8-4 與非門真值表
|
A |
B |
Y |
|
0 |
0 |
1 |
|
0 |
1 |
1 |
|
1 |
0 |
1 |
|
1 |
1 |
0 |
??? 與非門的邏輯功能用邏輯表達式描述,則為:
???????????????????????????????????????????  ??????????????????????? (8-4)
??????????????????????? (8-4)
??? 與非門可以有兩個或兩個以上的輸入端。
??? (2).或非門
???? 或非門的邏輯符號及波形圖如圖8-14所示。
??? 或非門的邏輯功能是:輸入全為0,輸出才為1;只要有一個輸入為1,輸出就為0。或非門真值表如表8-5所示。
???????????????????????????????????????????????????? 表8-5? 或非門真值表
|
A |
B |
Y |
|
0 |
0 |
1 |
|
0 |
1 |
0 |
|
1 |
0 |
0 |
|
1 |
1 |
0 |
??? 或非門的邏輯功能用邏輯表達式描述則為:
??????????????????????????????????????????????? 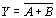 ??????????????? (8-5)
??????????????? (8-5)
??? 或非門也可有兩個或兩個以上的輸入端。?
?? (3).異或門
??? 異或門的邏輯符號及波形圖如圖8-15所示。
??? 其邏輯功能為:當兩個輸入端信號相同時,輸出為0;當兩個輸入端信號相異時,輸出為1。其真值表如表8-6所示。
???????????????????????????????????????????????????????????? 表8-6 異或門真值表
|
A |
B |
Y |
|
0 |
0 |
0 |
|
0 |
1 |
1 |
|
1 |
0 |
1 |
|
1 |
1 |
0 |
??? 異或門的邏輯功能用邏輯表達式描述為:
?????????????????????????????????????????? 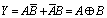 ?????????????? (8-6)
?????????????? (8-6)
??? 異或門只有兩個輸入端。
??? 思考與練習
??? 1.如果正邏輯改為負邏輯,那么正邏輯條件下的與門和或門的邏輯功能有何變化?
??? 2.假定一個電路中,指示燈Y和開關A、B、C的關系為 Y =AB+C
??? 試畫出相應的電路圖。??
- 門電路(39542)
相關推薦
邏輯門電路基本概念介紹
 366
366
邏輯門電路有關概念
 383
383
TTL門電路和CMOS有什么特點
 1392
1392邏輯門電路的原理及組成
 2377
2377邏輯門電路相關概念
 721
721
邏輯門電路的概念 幾種常見門電路的實現
 2557
2557
組合邏輯電路及其應用
 3
3數字電路中最基本的門電路
 1674
1674數字電路器件中最基本的門電路介紹
 17547
17547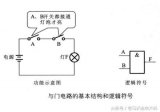
與、或、非門基礎門電路的特點
 26024
26024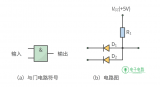
基于FPGA數字門電路的實現
 3053
3053
組合邏輯電路的學習教程課件免費下載
 15
15開路檢測電路中的門電路
 6159
6159數字電子技術與應用PDF版電子書免費下載
 129
129門電路作用是什么_門電路有幾種電路
 50544
50544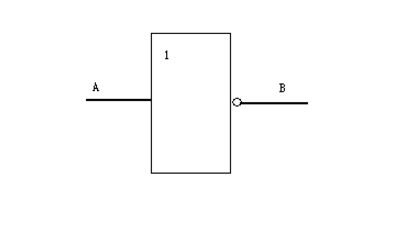
oc門電路特點及其功能
 42242
42242oc門電路圖分析詳解
 21983
21983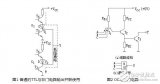
74LS00門電路及其運用
 0
0OC門電路及TSL門電路研究
 36
36十值TTL門電路的研究
 18
18常用基本邏輯門電路功能測試實驗
 29243
29243什么是門電路 門電路是什么意思
 43
43門電路邏輯功能測試與組合
 51
51組合邏輯電路中的競爭冒險
 10799
10799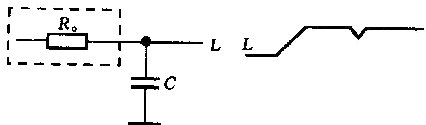
NMOS邏輯門電路
 7195
7195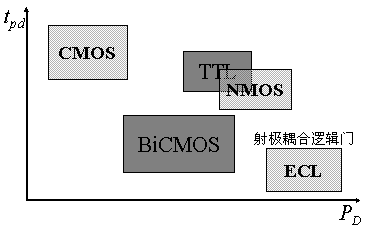
TTL邏輯門電路
 16065
16065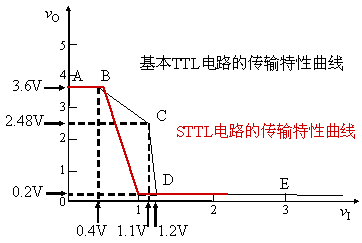
基本邏輯門電路
 17548
17548
CMOS邏輯門電路
 20263
20263
TTL門電路
 21561
21561
門電路和組合邏輯電路
 73
73組合邏輯電路設計實驗
 55
55邏輯門電路ppt
 69
69 電子發燒友App
電子發燒友App













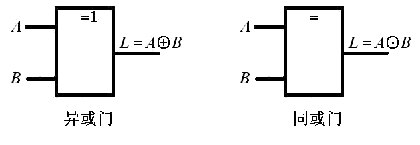
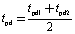










評論