1　引　言

　　滾珠螺母是滾珠絲杠副的內螺紋元件,它的精度直接影響滾珠絲杠副的傳動質量。因其摩擦小、效率高、運行平穩、壽命長、可逆傳動及零間隙等優點,廣泛應用于精密機械、機床、汽車、船舶、航空航天及計算機等行業。滾珠絲杠與螺母之間以鋼球為運動載體構成滾動摩擦,摩擦性能優良。由于螺母內表面結構較為復雜,無論設計還是制造工藝都比絲杠困難,尤其是它的內部參數較難測量。滾珠螺母的常規測量方法[1, 2]有固定式檢測儀、鋼珠接觸法及相對測量法,它們都屬于接觸測量,每種方法只能測量一種或兩種參數。有些參數能定量測量,有些則靠綜合量規檢定或透光法定性檢測,個別參數無法測量,螺母的形位誤差測量尤為困難。根據技術規范[2],滾珠螺母公稱直徑的圓度、滾道跳動及滾道對其外徑的同軸度應滿足一定的公差要求。由于滾珠螺母公稱直徑不同于普通光滑圓柱面,它是看不見且指針無法觸及到的虛擬要素,所以它的形位誤差無法用普通方法精確測量,目前的測量是以標準絲杠樣件為基準進行形位誤差測量,而絲杠本身存在誤差,導致測量結果的累積誤差較大,有些參數達不到要求。

　　本文提出一種改進的二次多項式插值法,將Canny邊緣檢測算子與3×3方向模板相結合確定邊緣方向,再利用Sobel邊緣檢測算子計算邊緣的亞像素位置,并推導了定位誤差公式,使CCD的分辨率提高40倍。計算測量了滾珠螺母的滾道圓度、圓柱度、徑向圓跳動及同軸度等形位誤差,誤差分別為f1=0. 013mm,f2=0. 016mm,f3=0. 022mm,f4=0. 014mm。在測量滾珠螺母的滾道圓度誤差時,提出了離散點非對稱分布在圓周附近時圓度誤差的最小區域評定方法。用簡單的解析方法論述了算法的實現過程,只需進行數次循環計算即可準確求出最小區域寬度(圓度誤差)。消除了方法誤差,減小了誤廢率,提高了測量精度。

　　2　輪廓邊緣分割

　　2.1　測量系統構成

　　測量系統主要由軟、硬件兩部分組成。其功能模塊分為圖像采集環節、處理環節、測量環節及結果分析幾部分。硬件部分包括CCD、工件及工作臺、計算機、接口卡及標定量塊等;軟件在VC++環境下自主開發,主要是圖像處理及后續測量的數據計算。

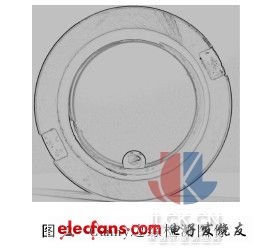
　　圖像質量直接影響檢測精度,本文采用大恒圖像公司生產的DH-HV3000FC彩色數字攝像頭,該攝像頭分辨率為2048×1536,像素尺寸為3. 2μm×3. 2μm, IEEE1394數字接口卡將采集到的數字圖像傳輸到計算機。采集圖像時,將直徑等于滾珠公稱直徑的標準測球放在滾道溝槽內,在重力作用下測球與光滑溝道最底部接觸。對采集到的彩色圖像進行灰度化處理,得到圖1所示的灰度圖像。

?

　　2.2　圖像分割

　　數字圖像存在一定噪聲,為獲得清晰的圖像輪廓,需對圖像進行降噪處理。均值濾波使圖像邊緣模糊,對幾何量測量誤差有較大影響。中值濾波對圖像中的顯著角點有影響。圖1中圖像的邊緣基本都是圓和圓弧曲線,個別角點對測量結果影響很小,所以采用3×3小鄰閾的中值濾波來消除個別毛刺噪聲的影響,效果較好。

　　圖像分割是圖像處理的重要內容,其目的是將目標從背景中分離出來。圖像分割主要分為閾值分割法和梯度分割法。閾值選取是閾值分割的關鍵,閾值選取過高,則過多的目標點被誤判為背景,閾值選取過低,又會使背景誤判為目標。梯度分割法[3, 4]獲得的邊界有時不是完全連通的,有一定程度的斷開,丟失了部分邊界像素,邊界連續性不好,

　　邊界定位不夠準確。有些微分邊緣檢測算子獲得的邊緣粗大,非邊界像素太多,給后續的圖像測量增加了難度。個別算子計算量較大、效率偏低,不適于實時測量要求。本文圖像是在實驗條件下采集的,經預處理噪聲已大為減少,利用Canny算子定位邊緣,該算子具有偏差最小、單向素寬、不丟失邊緣以及無虛假邊緣等優越性能,可提高邊緣的初始定位精度。圖2為Canny算子檢測到的邊緣,以此為基礎實施亞像素處理即可實現對參數的測量。

?

　　3　亞像素定位

　　亞像素定位技術是利用軟件算法來提高測量精度的有效途徑。亞像素定位的方法很多[3~7],插值是其中的一大類方法,多項式插值一般是通過邊緣檢測將邊緣定位到整像素位置,在水平方向和垂直方向做二次多項式插值,從而求出邊緣的精確位置。視覺測量中的圖像邊緣一般為階躍狀邊緣,邊緣的亞像素位置應垂直于邊緣,在梯度方向上度量。插值方法沒有考慮到像素點灰度的梯度方向,只在水平和垂直方向進行插值,所以這類方法存在誤差。

　　本文在Canny檢測的基礎上,計算出梯度方向,沿此方向對梯度圖像進行插值,確定邊緣的亞像素位置。Sobel算子可檢測邊緣的梯度,但在圖像中的噪聲較嚴重或圖像對比度較差等情況下,邊緣點的梯度存在較大誤差,導致檢測出的圓心誤差過大。

　　本文利用Canny檢測的初定位結果計算梯度方向。Canny邊緣檢測后得到一系列整像素邊緣點Pi(u,v),對孔的邊緣點,如果不考慮分辨率影響,Pi(u,v)應分布在理想圓(弧)上,此時梯度方向為半徑方向。設P0(u, v)為邊緣上的任意點,它的梯度幅值為R0(降噪后的灰度圖像進行Sobel邊緣檢測),沿邊緣方向(順時針方向)找到與其相鄰的兩個邊緣點P-1(u,v)、P1(u,v),邊緣方向的斜率為:

?

　　利用邊緣點P0(u,v)與梯度方向上的兩個相鄰插值點P0'和P0″的坐標及灰度梯度幅值即可計算邊緣點P0(u,v)的亞像素位置。設邊緣點P0(u,v)的灰度梯度幅值為R0,與P0(u,v)對應的梯度方向上兩個相鄰插值點P0'和P0″的灰度梯度幅值分別為R-1、R1,則邊緣點P0(u, v)的亞像素位置偏移為:

?

　　4　形位誤差測量

　　本文所測為P級精度的滾珠螺母GQ25×6,文獻[2]給出了其技術規范。現對其滾道圓度誤差、圓柱度誤差、跳動誤差及同軸度誤差等參數進行測量。

　　4.1　滾道圓度誤差測量

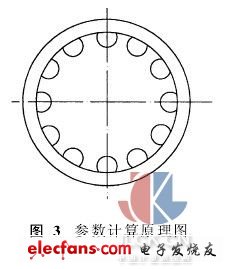
　　將內螺紋裝卡在分度頭上,標準測球放置在滾道內,在一個螺距范圍內采集N個圖像,使每兩次采集圖像之間螺母沿固定方向旋轉360°/N,計算度量測球中心點(X0,Y0)和螺母外圓柱面中心點(Xb,Yb)的亞像素坐標,以此計算形位誤差。由于內螺紋外圓柱面的加工精度較高,形狀誤差很小,故將其視為理想圓柱面,在N個圖像中,其中心的位置相對于圓周像素保持不變。以螺母外圓柱面為基準,將各圖像測球中心坐標通過外圓柱面中心坐標和標定系數統一在一個坐標中,如圖3所示。

?

　　坐標變換的步驟是:首先對圖像i (i=1,2,…,N)進行平移,使內螺紋外圓柱面中心與坐標原點重合;其次選擇某個標定系數進行比例變換,使N個圖像中的零件(以外圓半徑為準)具有相同的像素數;然后將圖像以原點為中心旋轉360°(N-i) /N;最后平移回到原始位置(采集位置)。可根據各個測球中心坐標在統一坐標系中的位置求得圓度誤差。

　　本文用解析方法確定各測球的分布中心(評定圓度的基準),使滾道圓度誤差的評定符合最小區域法。設某一螺距范圍內所有測球的球心坐標為(X0i, Y0i)(i=1,2,…,N),它們在端面上的理想分布應當在一個圓上。事實上,由于內螺紋滾道及測球的加工誤差及測量誤差,它們的分布是有誤差的。以N個測球球心坐標(X0i, Y0i)為擬合點,利用解析方法求出測球中心分布圓的圓心(X0*, Y0*),使其在評定圓度誤差時滿足最小區域原則。算法步驟如下:

?

　　=m+1,m+2,…,N+i-1),構造直線方程L′。

　　(2)分別求L與L′垂直平分線的交點Ow,以該點為圓心經過4個點做兩個圓,其半徑差即為最小區域法評定的4個點的圓度誤差。應時時判斷每一次計算的圓度誤差,滿足最小區域條件時即停止計算,此時的圓心Ow即為最小區域圓圓心(X0*,Y0*),否則轉步驟(3)繼續計算。

　　(3)i從1到N做循環,返回步驟1重復計算。上述循環計算中,從外到內的循環次序是i-g-m-k。滿足最小區域條件時,最小區域圓圓心至各測球中心距離中,至少各有兩個最大值Rmax及兩個最小值Rmin,且兩最大值坐標點連線與兩最小值坐標點連線的交點在最小圓內(最大值點與最小值點相互交替)。最小區域圓圓心(X0*, Y0*)至(X0i, Y0i)的最遠點(Xmax,Ymax)距離與最近點(Xmin,Ymin)距離之差即為圓度誤差,用下式表示:

?

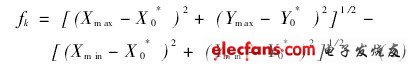
　　在內螺紋整個滾道內確定M個假想截面位置,重復測量每個位置的圓度誤差,取最大值作為內螺紋公稱直徑的圓度誤差。

　　4.2　滾道圓柱度誤差測量

　　在圓度誤差計算中,已經獲得了M個位置的測球分布中心(X0i*, Y0i*)(i=1,2,…,M)。同計算圓度采取的方法相同,將M個位置的數據統一在一個坐標中,共得到N×M個測球中心坐標,對它們進行圓度計算,可得到內螺紋公稱直徑圓柱度誤差。

　　4.3　滾道同軸度誤差測量

　　同軸度誤差是一種位置誤差,它是指被測軸線對基準軸線的變動量。在圓柱度誤差測量中,M個截面位置的測球分布中心(X0i*, Y0i*)是變化的,它的離散軌跡體現了被測軸線,而內螺紋外圓柱面的中心(Xb, Yb)是基準軸線。根據同軸度誤差的最小區域評定法則, (X0i*, Y0i*)與(Xb, Yb)距離的最大值的兩倍為內螺紋公稱直徑對其外徑的同軸度誤差。

　　4.4　滾道圓跳動誤差測量

　　在圓度誤差及圓柱度誤差測量中,測球球心坐標(X0i, Y0i)及螺母外圓柱面中心(Xb, Yb)已經求出,根據定義,分別計算(X0i, Y0i)至(Xb, Yb)的距離Ri,則該截面滾道圓跳動誤差為Rimax-Rimin。求解全部M個截面的圓跳動誤差,其最大值即為內螺紋滾道對基準(內螺紋外圓柱面軸線)的徑向圓跳動誤差。

　　4.5　實驗

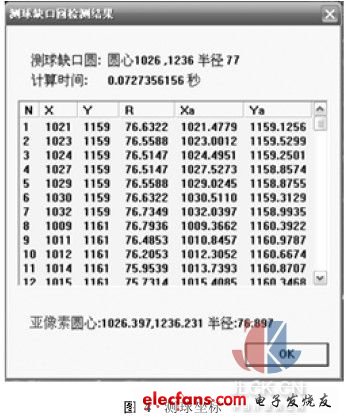
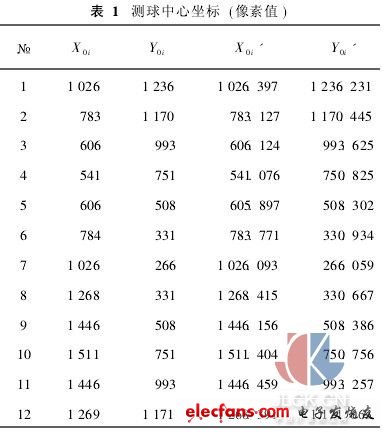
　　本實驗依據提取的邊緣,應用開發軟件按前述幾何參數的計算方法,測量了內螺紋滾道的形位誤差。采集6個滾道截面進行測量(M=6),每個滾道截面采集12個圖像(N=12)。圖4為測球邊緣坐標和中心坐標(X0i, Y0i) (i=1,2,…,N)及其亞像素值(X0i', Y0i'),內螺紋外圓柱面的亞像素中心坐標(Xb, Yb)為(1026.349,751.128)(像素值)。計算出一個螺距范圍內12幅圖像的測球參數,以螺母外圓柱中心為基準經過旋轉、平移等變換統一到一個坐標系中,結果(像素值)如表1所示。

?

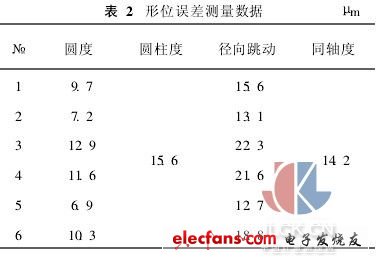
　　根據表1中數據,由整像素坐標按前述最小區域評定法求得圓度誤差為: f=0.731,最小區域圓圓心坐標為(1026.134,750.866);而根據亞像素坐標求得的圓度誤差為: f=0.449,最小區域圓圓心坐標為(1026.210,750.920)。該圖像的標定系數k=0.025 8,按整像素計算圓度誤差為0.731mm×0. 025 8= 0. 018 9mm,按亞像素計算圓度誤差為0. 449mm×0. 025 8=0. 0116mm。對應表1中的數據,求各個測球中心至螺母外徑中心之間的距離,其最大差值作為徑向圓跳動誤差值,計算結果為21. 6μm。最小區域圓圓心至螺母外徑中心之間距離的2倍為該截面滾道中心相對于基準軸線的同心度誤差,計算值為12. 9μm。6次亞像素測量結果見表2。

?

?

　　所測螺母形位誤差結果為:圓度誤差為0. 013mm,圓柱度誤差為0. 016 mm,徑向跳動誤差為0. 022 mm,同軸度誤差0. 014 mm。由文獻[2]可知,本文所測螺母的幾何尺寸及形位誤差項目中,除圓度誤差(公差為12μm)外,其余均符合技術要求。

　　5　誤差分析

　　引起測量誤差的主要因素有系統分辨率、幾何畸變和各種噪聲[8]。體現在以下幾方面:

　　(1) CCD誤差。本文使用的CCD像元間距為3.2μm,其誤差也為3. 2μm。由于采用了新的亞像素技術,定位誤差理論上可達到整像素的1/42(約為3. 2/42≈0. 076μm),相當于將CCD的分辨率提高了42倍。被測零件的外形尺寸為44 mm×40mm,CCD分辨率為2 048×1 536,整像素對應尺寸0. 026mm,亞像素對應尺寸為0. 62μm。

　　(2)標定誤差。由于制造、安裝等原因,攝像機光學系統并不是精確地按理想化的小孔成像原理工作,存在透鏡畸變[9]。本文采用TEC-M55焦闌鏡頭(遠心鏡頭),畸變系數很小,經過用5mm標準量塊實際測定,圖像范圍內各處水平及垂直方向量塊寬度整像素誤差未檢測到。采用相對標定法,標定時對畸變進行了矯正。標準樣件尺寸由萬能工具顯微鏡測得,其外徑為?40. 008 mm。由于使用標準的檢測對象作為標定參照物,不需要標定攝像機的內外參數,只需要標定出攝像機的物面分辨率,簡化了標定過程,保證了標定精度和穩定性。

　　(3)其它誤差。電源電壓的波動也對測量結果產生一定的影響,本文利用直流穩壓電源供電,減少了電壓的波動。此外,在CCD攝像機、A/D轉換器及采集電路中存在熱電子噪聲,使采集圖像的屏幕上有許多閃爍跳躍的斑點和波紋。利用濾波和多次測量取平均值可抑制和減弱該噪聲,本文首先采集6幅相同的圖像將其平均,大大減少了加性噪聲,然后對圖像進行了中值濾波。最后對某些參數多次測量,取平均值作為測量結果,減少了誤差。測量過程中無法真實獲取某一截面中的數值,因為滾道是螺旋面而不是圓環面,用一個螺距內的誤差值來表示某一截面的誤差將放大圓度誤差。另一方面,截取若干螺距內的滾道代替整個滾道,且用有限個測球中心坐標代替螺距內一周的坐標數據,可能使得所測參數小于實際誤差數值從而減小誤差。通過在不同位置反復測試,可知這兩種誤差很小,且兩者的綜合作用可以抵消一部分誤差,使得實際誤差進一步減小。

　　6　結果與討論

　　本文基于CCD技術對滾珠螺母進行了直接定量測量。計算出其公稱直徑的形位誤差,測量過程與螺母的工作情況相似,影響測量結果的因素很少。測量時產生的誤差可以抵消一部分,使得實際誤差較小。

　　常規測量方法是打表法,由于指針無法觸及被測螺母的公稱直徑表面,只能將被測滾珠螺母與標準絲杠旋合,通過間接方法計算誤差,評定時不考慮其它環節誤差。這種測量方法首先要求特制標準絲杠,給檢測帶來不便,同時絲杠的誤差不可避免地要帶入測量結果。不同尺寸的螺母要求相應的標準絲杠與其匹配進行測量,這就需要大量的標準絲杠,既不經濟也不便于管理。其次,滾珠絲杠與螺母之間存在間隙,也會影響測量精度。另外,表頭誤差及指針方向偏差均會降低測量精度。

　　本文所述測量方法符合測量原理,在眾多誤差來源中,測量誤差主要來自光學系統的誤差。光學系統的誤差主要是透鏡像差、感光像元排列誤差和透視誤差。成像系統的幾何畸變誤差是典型的系統誤差,它是多種誤差的組合,是影響光學測量精度的關鍵因素之一,提高系統分辨率及采取各種標定方法能有效降低系統誤差。本文測量方法適合類似圓柱及圓錐內表面零件等接觸測量難以處理的零件。

　　7　結　論

　　(1)構建了滾珠螺母視覺檢測系統的硬件結構,開發了相應的測量軟件。用定量的方法進行了直接測量,為滾珠螺母形位誤差測量提供了一種新的方法。

　　(2)為提高圖像定位精度,提出了改進的二次多項式插值方法,大大提高了圖像邊緣的定位精度。

　　(3)在計算圓度誤差時,提出了圓的邊緣點離散分布時圓度誤差的最小區域評定解析計算方法,只需進行數次循環計算即可準確求出最小區域寬度(圓度誤差)。而最小二乘法只適合求解連續數據的完整圓或離散數據的對稱數據。本文所述算法消除了方法誤差,提高了測量精度。