?
雖然在較低頻率下可以較輕松地檢查一個簡單放大器的穩定性,但評估一個較為復雜的電路是否穩定,難度可能會大得多。本文使用常見的Pspice宏模型結合一些簡單的電路設計技巧來提高設計工程師的設計能力,以確保其設計的實用性與穩定性。
導致放大器不穩定的原因
在任何相關頻率下,只要環路增益不轉變為正反饋,則閉環系統穩定。環路增益是一個相量,因而具有幅度和相位特性。環路由理想的負反饋轉變為正反饋所帶來的額外相移即是最常見的不穩定因素。環路增益相位的“相關”頻率,一般出現在環路增益大于或等于0dB之處。
?
圖1:總等效噪聲密度-反饋電阻關系曲線。
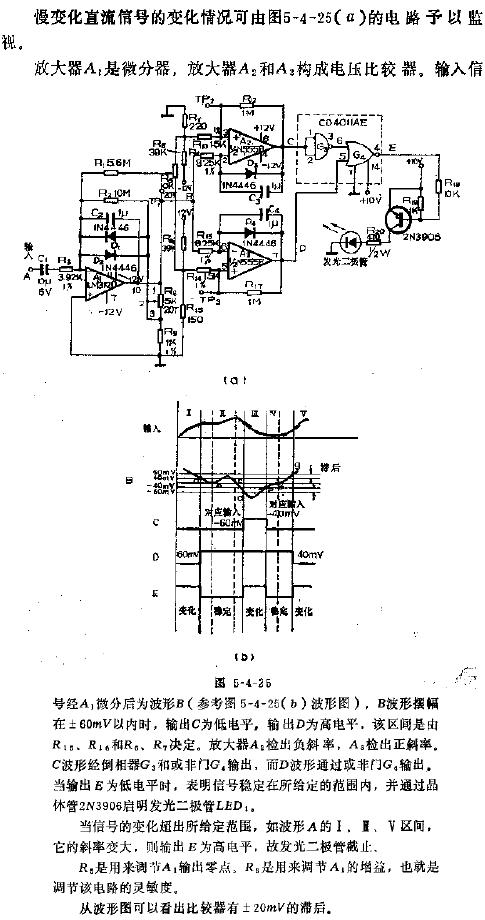
如圖2所示的放大器電路,通過斷開環路,測量信號在環路中傳播一次所產生的相移,即可推算出電路的穩定情況。以下例子介紹的方法可利用仿真軟件,運算放大器宏模型以及Pspice提供的理想元器件來實現。
?
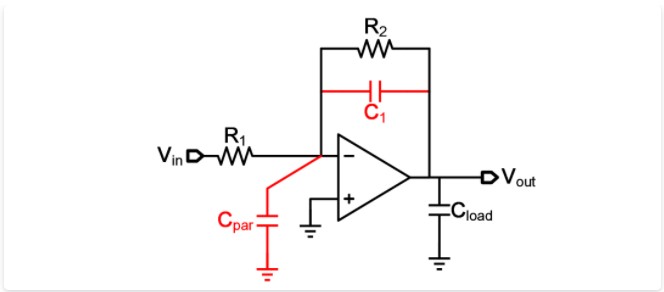
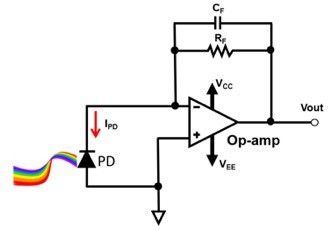
圖2:跨阻抗放大器。
高速低噪聲跨阻放大器(TIA)穩定性示例
我們以一個跨阻放大器(TIA)為例,通過分析其穩定性來闡述我們將要推薦的技術。TIA廣泛應用在工業領域和消費領域,例如LIDAR(光探測和測距)、條形碼掃描儀、工廠自動化等。設計工程師遇到的挑戰是,在不會造成衰減和老化的情況下,如何最大化信噪比(SNR),以及如何獲得足夠的速度/帶寬來傳遞所需的信號。圖2為采用了LMH6629的放大器示意圖,這款超高速(GBWP=4GHz)低噪聲(0.69nV/RtHz)器件具有+10V/V的最小穩定增益(COMP引腳連至VCC)的。LMH6629的補償(COMP)輸入可以連至VEE,從而進一步將最小穩定增益降低到4V/V。
為獲得最大的轉換速率和帶寬(小信號和大信號),在這個例子中,COMP引腳被連接到VCC。可獲得的帶寬與放大器GBWP直接相關,與跨阻增益(RF)和光電二極管內的寄生電容成反比。確定一個給定放大器所使用的反饋電阻(RF)有一個簡單方便的辦法:在使用了LMH6629的情況下,總等效輸入電流噪聲密度“ini”與RF的關系如圖1中曲線所示。圖中的“in”是LMH6629的輸入噪聲電流,“en”是LMH6629的輸入噪聲電壓,“k”是波爾茲曼常數,而“T”是用℃表示的絕對溫度。
由圖1可知,對于LMH6629而言,將RF設定為10k?確保了最小的總等效輸入電流噪聲密度ini,由此也可以得到最高的SNR。RF的進一步增加會降低可獲取的最大速度,而SNR不會得到明顯改善。
是什么使得一個看起來很簡單的電路的穩定性分析變得如此復雜呢?主要原因就是寄生元件的影響。在圖2的電路中,幾乎沒有跡象表明這個電路會是不穩定的,圖中所示的寄生元件“CD”是光電二極管固有電容,其實際大小由光電二極管的面積和靈敏度來決定。R2用于消除LMH6629的輸入偏置電流產生的偏移誤差,同時C2消除了R2的噪聲。
假設一個光電二極管標稱電容(CD)為10pF,圖2中電路的仿真響應如圖3所示,由此可以判斷出電路是不穩定的:其頻率響應曲線中大而尖的峰值即為證明。在頻域內,通過了解電路的相位裕度(PM)就可以確定電路的穩定性。為便于仿真,可將光電二極管的電路簡化等效為一個電流源。
?
圖3:TIA頻率響應示意電路的不穩定性。
對于一個富有經驗的用戶來說,當一個具有較大反饋電阻RF的系統不穩定時,意味著RF“尋找”運算放大器反向輸入端的寄生電容,是產生振鈴和過沖的原因。在環路中,這種現象可稱為“過相移”。反向輸入寄生電容由光電二極管電容和LMH6629輸入電容組成。LMH6629的更高帶寬令問題進一步惡化——總輸入電容的降低將足以引起過相移。對于這種情況,最有效的補救方法是在RF兩端并聯一個合適的電容(CF)。
為找出導致這一現象中低相位裕度的原因,除了全面的筆頭分析,設計人員只能反復試驗,通過選擇合適的補償元件來提高系統的穩定性。一個更嚴密的辦法就是通過仿真來獲取對各種頻率下環路特性的更深入了解。這種辦法比起筆頭分析法要快得多,既不需要復雜的運算,也不會帶來計算錯誤的可能。設計人員要做的是在開環情況下觀察電路,以便了解環路增益(LG)的幅度和相位情況。仿真操作為用戶提供了能進行高效分析的各種理想元件,從而使得上述分析成為可能。
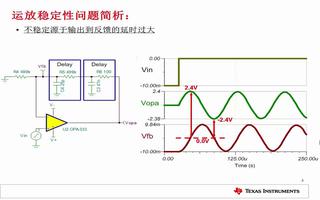
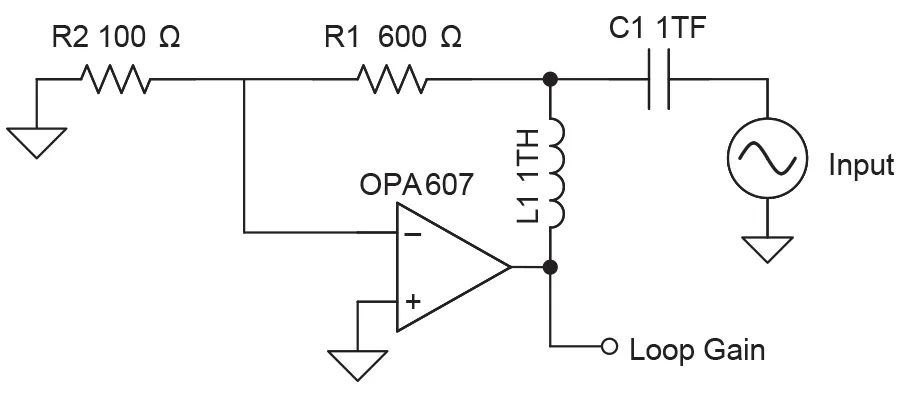
在圖4的仿真電路中,環路已在AC(與相位裕度有關)處斷開,同時保留DC閉環,以建立合適的操作點。在輸出處用一個大串聯電感(L1)和一個大并聯電容(C1)即可完成仿真。
?
圖4:為了進行仿真,插入大“L”和“C”以斷開AC環路。
驅動大電容(V_Drive)的交流電源可以設定為1V,在器件輸出端,仿真響應如圖5中的LG函數所示。圖5中的0o低相位裕度印證了圖3中過高的閉環頻率響應峰值。為確保電路的穩定性,對應的品質因數即相位裕度應大于45o。
?
圖5:開環曲線表明相位裕度不足。
請注意:在頻率響應仿真開始之前,請確保將輸入電流源(取代光電二極管)設定為“AC 0”;顯示結果需將CF設為0pF;圖5中幅度用實線表示,相位角用虛線表示;當相位裕度為0dB時,相位裕度對應LG函數的相位角。
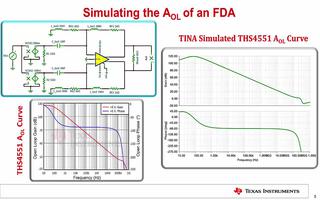
如圖6所示,為找到合適的補償電容值來改善相位裕度,我們可以將針對不同的CF值(圖4電路)的噪聲增益曲線和LMH6629開環增益曲線放在一起。噪聲增益為V(Drive)/V(In_Neg)。請注意LG的仿真低頻值要大于0dB,因為LMH6629的宏模型還包括了其差分輸入電阻。
?
圖6:CF最優化噪聲增益曲線。
大部分Pspice仿真器都允許使用圖6所示的“.STEP PARAM”語句來進行多級仿真并顯示迭加的結果。其它仿真器可能有專用命令來實現此類同步仿真功能。最優CF值在噪聲增益函數與LMH6629的開環增益曲線相交頻率處給噪聲增益函數設置了一個極點。由圖6可知,在本例中,CF=0.25pF。
大于0.25pF的更高CF值將會帶來帶寬損失,相應地,若CF低于0.25pF,相位裕度又將不足。如果CF足夠高(本例中是7pF),噪聲增益曲線有可能在低于20dB處與開環曲線相交。20dB是LMH6629的最小穩定增益。這種情況下電路可能將不再穩定或者放大器可能出現過高頻率響應峰值。因此必須有一個穩定范圍和最優值。
圖7所示的是當CF=0.25pF時,頻率函數LG的結果曲線。在沒有CF的情況下,相位裕度從原來的0o增加到61o。
?
圖7:開環曲線繪制驗證CF令相位裕度得以改善。
找到最優CF值后,可以重新查看初始的閉環配置(沒有大電感和電容加入到LG和NG的研究中),在使用最優CF值(此時是0.25pF)的情況下可以得到階躍響應。圖8顯示了面向不同CF的響應曲線,證實了CF值不論是偏大或是偏小,都會造成系統的不穩定,或是振鈴時間和穩定時間的延長;而最優CF值可以在最小振鈴下實現非常好的階躍響應。顯然,無論CF取值0pF還是7pF,電路都非常地不穩定。這表明7pF時的振蕩頻率遠高于0pF時的振蕩頻率,并不是因為噪聲增益與放大器開環增益曲線的交接頻率較高(如圖6所預測的那樣)。
?
圖8:不同CF對應的閉環階躍響應。
實際考慮和實驗結果比較
利用基于Pspice的分析方法來研究合適的補償值,并通過仿真找到最佳響應時的參數值后,接下來就是在實驗臺上驗證仿真結果。圖9為一個實驗臺的驗證設置示意圖。
?
圖9:TIA補償實驗臺驗證設置。
以下是圖9實驗臺設置的一些要點。
低電容值和實驗臺優化:為降低有效電容值,可以將RA、RB串在一起并與CF鄰接,這樣可以用一個市場上容易找到的電容(>1pF)來獲取皮法以下的電容值,而該值很難直接獲得。只要RB << RF,該電路即可將CF的等效電容值降低1+ RB/RA倍。該方法可以得到一個0.20pF的等效電容,選用這樣的設置是因為0.25pF的仿真值會產生過阻尼實驗臺響應。物理電路板會存在一定的寄生電感和電容,它們可以被最小化,但是不能完全降低到0。因此,人們希望通過實驗臺測試來促進對仿真結果的優化,特別是在處理皮法級以下的標稱值時。等效電容為0.20pF時,檢測到的帶寬為70MHz;而當等效電容為0.25pF時,帶寬下降至55MHz。
等效光電二極管實驗臺設置:為便于測試,所示的(Rin, Cin以及CD)前端配置允許使用標準的50?實驗室設備來模擬光電二極管的性能。這里CD(假設為光電二極管電容)被設定為10pF。
?
圖10:CF_eq=0.2pF時測定的頻率響應。
圖10和圖11分別顯示了使用50?源和輸出端負載得到的頻率響應和階躍響應結果。如圖所示,-3dB帶寬時,頻率接近70MHz,沒有峰值。階躍響應曲線在上升時間和下降時間與頻率響應相匹配,圖中顯示了最小過沖值,沒有振鈴,從而可以確定電路已被正確地補償。為了對仿真作進一步確認,實驗臺測試驗證了在沒有補償電容時出現的大峰值以及10pF電容跨接RF時所產生的全振蕩過程。
?
圖11:CF_eq=0.2pF時測定的階躍響應。
測量結果被證實是可靠的,充分補償了70MHz的帶寬,符合方程式1中的理論值,該方程式中CIN為總反向輸入電容(包括二極管和運算放大器)。
?
通過斷開環路,并借助Pspice的迭代函數(即階躍函數),人們就能在很短的時間內更好地尋找最優補償方法,實現環路的穩定性。本文的例子充分說明了該方法的簡便和靈活性。當然,本文所用的運算放大器的宏模型必須對器件精確建模(包括輸入階段的寄生效應),否則獲得的結果就有可能遠遠偏離實際值。這個例子所演示的技術并非僅適用于TIA電路(這只是選取出來的一個具有代表性的例子),實際上該技術也可應用于大多數放大器電路上。
 電子發燒友App
電子發燒友App


























評論